呼和浩特专版2020中考数学复习方案第二单元方程组与不等式组第08课时一元二次方程及其应用课件 46页

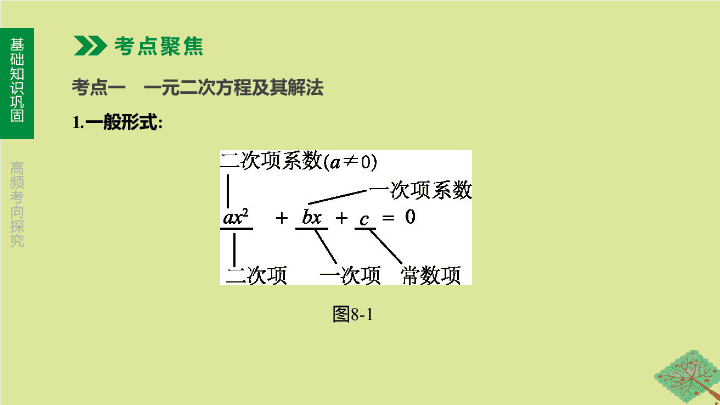
第 8 课时 一元二次方程及其应用 第二单元　方程 ( 组 ) 与不等式 ( 组 ) 考点一　一元二次方程及其解法 考点聚焦 1 . 一般形式 : 图 8-1 2 . 一元二次方程的解法 （续表） 考点二　一元二次方程根的判别式、根与系数的关系 1 . 判别式与根的关系 (1) b 2 -4 ac> 0⇔ 方程有 ④ 　　　 　 的实数根 ; (2) b 2 -4 ac= 0⇔ 方程有 ⑤ 　 　　　 的实数根 ;  (3) b 2 -4 ac< 0⇔ 方程 ⑥ 　　　　 实数根 .  2 . 根与系数的关系 ( 选学 ) 若关于 x 的一元二次方程 ax 2 + bx + c= 0( a ≠0) 的两根分别为 x 1 , x 2 , 则 x 1 + x 2 = ⑦ 　　　　 , x 1 x 2 = ⑧ 　　　　 .  两个不相等 两个相等 没有 考点三　一元二次方程的实际应用 应用类型 等量关系 增长率问题 (1) 增长率 = 增量 ÷ 基础量 ; (2) 设 a 为原来的量 , m 为平均增长率 , n 为增长次数 , b 为增长后的量 , 则 a (1+ m ) n =b 销售利润问题 (1) 纯利润 = 售出价 - 进货价 - 其他费用 ; (2) 利润率 = 利润 ÷ 进货价 ×100%; (3) 总利润 = ( 售价 - 成本 )× 数量 （续表） 应用类型 等量关系 面积问题 AB + BC + CD=a S 阴影 = ⑨ 　   S 阴影 = ⑩ 　   S 阴影 = ⑪   ( a -2 x )( b -2 x ) ( a - x )( b - x ) 题组一　必会题 对点演练 25 5 36 6 2 . [ 九上 P21 习题 21 . 3 第 1(1)(3)(4) 题改编 ] (1) 方程 x 2 +10 x +21 = 0 的解是 　　　　 　 ;  (2) 方程 3 x 2 +6 x -4 = 0 的解是 　　　　 　　 ;  (3) 方程 3 x ( x +1) = 3 x +3 的解是 　　　　　　　 .  x 1 = -3, x 2 = -7 x 1 = -1, x 2 = 1 3 . [ 九上 P22 习题 21 . 3 第 6 题改编 ] 参加足球联赛的每两队之间都进行两场比赛 , 共要比赛 90 场 , 共有 　　　　 个队参加比赛 .  [ 答案 ]10 [ 解析 ] 设参加比赛的球队共有 x 个 . 由题意得 x ( x -1) = 90,( x -10)( x +9) = 0, 解得 x 1 = 10, x 2 = -9( 不合题意 , 舍去 ) . 所以参加比赛的球队共有 10 个 . 4 . 股票每天的涨、跌幅均不超过 10%, 即当涨了原价的 10% 后 , 便不能再涨 , 叫涨停 ; 当跌了原价的 10% 后 , 便不能再跌 , 叫跌停 . 已知一支股票某天跌停 , 之后两天时间又涨回到原价 , 若这两天此股票股价的平均增长率为 x , 则 x 满足的方程是 　　　　　　 .  5 . [ 九上 P25 复习题 21 第 4 题改编 ] 写出下列方程两个根的和与积 : (1) x 2 -5 x -10 = 0, x 1 + x 2 = 　　　　 , x 1 x 2 = 　　　　 ;  (2)2 x 2 +7 x +1 = 0, x 1 + x 2 = 　　　　 , x 1 x 2 = 　　　　 ;  (3)3 x 2 -1 = 2 x +5, x 1 + x 2 = 　　　　 , x 1 x 2 = 　　　　 ;  (4) x ( x -1) = 3 x +7, x 1 + x 2 = 　　　　 , x 1 x 2 = 　　　　 .  5 -10 -2 4 -7 题组二　易错题 【 失分点 】 解一元二次方程时 , 方程的两边直接除以相同的整式 , 导致漏解 ; 在运用根的判别式或者根与系数的关系时 , 忽视二次项系数不能等于 0 这一条件 . x= 1 或 x= 2 7 . [2019· 枣庄 ] 已知关于 x 的方程 ax 2 +2 x -3 = 0 有两个不相等的实数根 , 则 a 的取值范围 是 　　　　 .  考向一　一元二次方程的解法 例 1 用指定方法解方程 x 2 -12 x +27 = 0 . (1) 公式法 : (2) 配方法 : (3) 因式分解法 : 例 1 用指定方法解方程 x 2 -12 x +27 = 0 . (2) 配方法 : 例 1 用指定方法解方程 x 2 -12 x +27 = 0 . (3) 因式分解法 : 【 方法点析 】 解一元二次方程要根据方程的特点选取方法 , 考虑选用的先后顺序为直接开平方法、因式分解法、公式法、配方法 . 形如 ( x + a ) 2 =b 的一元二次方程可直接开平方 ; 若一元二次方程的一边是 0, 而另一边又能分解成两个一次因式的积 , 则用因式分解法 ; 当二次项系数为 1, 且一次项系数为偶数时 , 可用配方法 . | 考向精练 | 1 . [2019· 怀化 ] 一元二次方程 x 2 +2 x +1 = 0 的解是 ( 　　 ) A .x 1 = 1, x 2 = -1 B .x 1 =x 2 = 1 C .x 1 =x 2 = -1 D .x 1 = -1, x 2 = 2 C [ 答案 ]4 3 . [2019· 呼和浩特 19 题 ] 用配方法求一元二次方程 (2 x +3)( x -6) = 16 的实数根 . 4 . [2017· 呼和浩特实验教育集团第一学期期中 ] 阅读理解题 : 我们知道一元二次方程是转化为一元一次方程来解的 , 例如 : 解方程 x 2 -2 x= 0, 通过因式分解将方程化为 x ( x -2) = 0, 从而得到 x= 0 和 x -2 = 0 两个一元一次方程 , 通过解这两个一元一次方程 , 求得原方程的解 . (1) 利用上述方法解一元二次不等式 :2 x ( x -1)-3( x -1) < 0; (2) 利用函数的观点解一元二次不等式 x 2 +6 x +5 > 0 . 4 . [2017· 呼和浩特实验教育集团第一学期期中 ] 阅读理解题 : 我们知道一元二次方程是转化为一元一次方程来解的 , 例如 : 解方程 x 2 -2 x= 0, 通过因式分解将方程化为 x ( x -2) = 0, 从而得到 x= 0 和 x -2 = 0 两个一元一次方程 , 通过解这两个一元一次方程 , 求得原方程的解 . (2) 利用函数的观点解一元二次不等式 x 2 +6 x +5 > 0 . 考向二　一元二次方程根的判别式 例 2 已知关于 x 的一元二次方程 ( m -1) x 2 -(2 m +1) x + m= 0, 当 m 分别取何值时 , 满足下列条件 : (1) 方程有两个不相等的实数根 ; (2) 方程有两个相等的实数根 , 并求出根 ; (3) 方程没有实数根 . 例 2 已知关于 x 的一元二次方程 ( m -1) x 2 -(2 m +1) x + m= 0, 当 m 分别取何值时 , 满足下列条件 : (2) 方程有两个相等的实数根 , 并求出根 ; 例 2 已知关于 x 的一元二次方程 ( m -1) x 2 -(2 m +1) x + m= 0, 当 m 分别取何值时 , 满足下列条件 : (3) 方程没有实数根 . 【 方法点析 】 (1) 时刻牢记隐含条件 : 二次项系数不为 0 . (2) 在计算前应先将方程化为一般式 , 再利用 “ b 2 -4 ac ” 判断 . | 考向精练 | [ 答案 ] C 2 . [2017 呼和浩特一模 ] 已知 a , b , c 为常数 , 且 ( a - c ) 2 >a 2 + c 2 , 则关于 x 的方程 ax 2 + bx + c= 0 根的情况是 ( 　　 ) A . 有两个相等的实数根 B . 有两个不相等的实数根 C . 不确定 , 与 b 的取值有关 D . 无实数根 B [ 答案 ] C 考向三　一元二次方程根与系数的关系 | 考向精练 | A 2 . [2017· 呼和浩特 5 题 ] 若关于 x 的一元二次方程 x 2 +( a 2 -2 a ) x + a -1 = 0 的两个实数根互为相反数 , 则 a 的值为 ( 　　 ) A . 2 B . 0 C . 1 D . 2 或 0 [ 答案 ] B 3 . [2019· 启秀中学初三数学二模 ] 已知关于 x 的一元二次方程 x 2 -4 x + m -1 = 0 的实数根 x 1 , x 2 满足 3 x 1 x 2 - x 1 - x 2 > 2, 则 m 的取值范围是 　　　　 .  3