呼和浩特专版2020中考数学复习方案第四单元三角形课时训练16几何初步及平行线相交线试题 8页

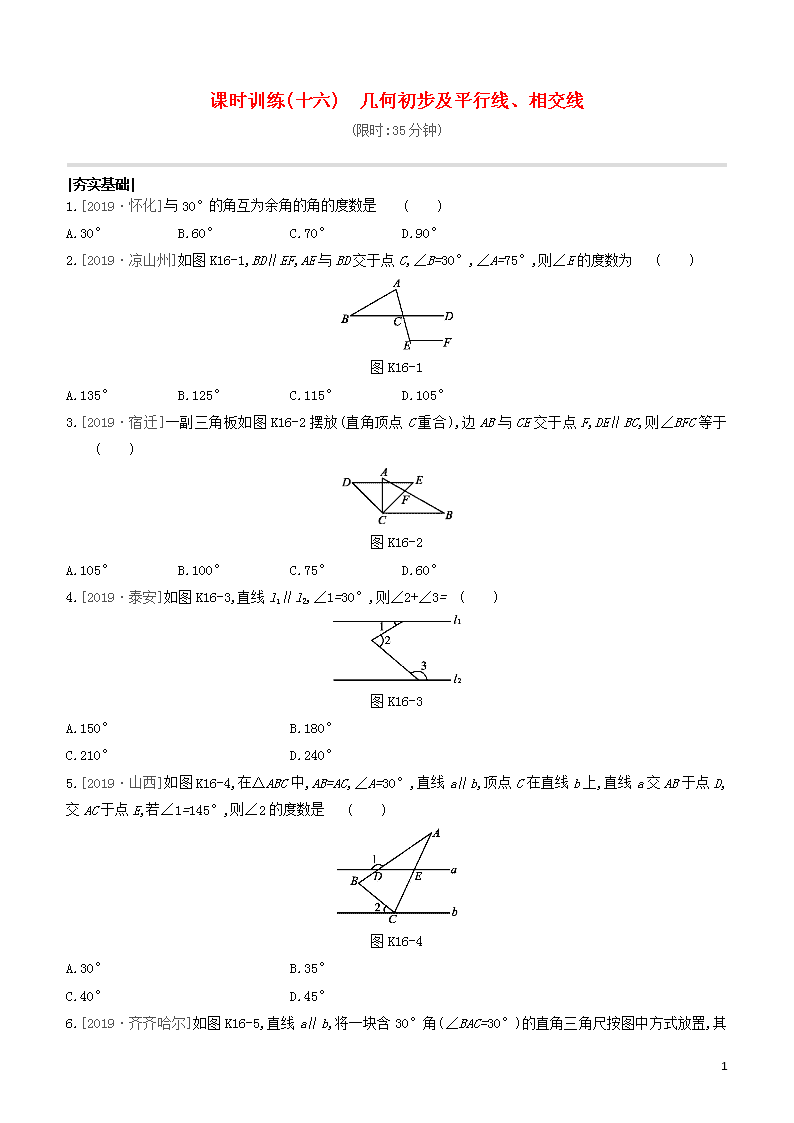
课时训练(十六)　几何初步及平行线、相交线 ‎(限时:35分钟)‎ ‎|夯实基础|‎ ‎1.[2019·怀化]与30°的角互为余角的角的度数是 (　　)‎ A.30° B.60° C.70° D.90°‎ ‎2.[2019·凉山州]如图K16-1,BD∥EF,AE与BD交于点C,∠B=30°,∠A=75°,则∠E的度数为 (　　)‎ 图K16-1‎ A.135° B.125° C.115° D.105°‎ ‎3.[2019·宿迁]一副三角板如图K16-2摆放(直角顶点C重合),边AB与CE交于点F,DE∥BC,则∠BFC等于 (　　)‎ 图K16-2‎ A.105° B.100° C.75° D.60°‎ ‎4.[2019·泰安]如图K16-3,直线l1∥l2,∠1=30°,则∠2+∠3= (　　)‎ 图K16-3‎ A.150° B.180° ‎ C.210° D.240°‎ ‎5.[2019·山西]如图K16-4,在△ABC中,AB=AC,∠A=30°,直线a∥b,顶点C在直线b上,直线a交AB于点D,交AC于点E,若∠1=145°,则∠2的度数是 (　　)‎ 图K16-4‎ A.30° B.35° ‎ C.40° D.45°‎ ‎6.[2019·齐齐哈尔]如图K16-5,直线a∥b,将一块含30°角(∠BAC=30°)的直角三角尺按图中方式放置,其 8‎ 中A和C两点分别落在直线a和b上,若∠1=20°,则∠2的度数为 (　　)‎ 图K16-5‎ A.20° B.30° ‎ C.40° D.50°‎ ‎7.[2019·东营]将一副三角板(∠A=30°,∠E=45°)按如图K16-6所示方式摆放,使得BA∥EF,则∠AOF等于 (　　)‎ 图K16-6‎ A.75° B.90°‎ C.105° D.115°‎ ‎8.[2019·梧州]如图K16-7,钟表上10点整时,时针与分针所成的角是 (　　)‎ 图K16-7‎ A.30° ‎ B.60°‎ C.90° ‎ D.120°‎ ‎9.[2019·广州]如图K16-8,点A,B,C在直线l上,PB⊥l,PA=6 cm,PB=5 cm,PC=7 cm,则点P到直线l的距离是 ‎　　　　cm. ‎ 图K16-8‎ ‎10.[2019·柳州]如图K16-9,若AB∥CD,则在图中所标注的角中,一定相等的角是　　　　. 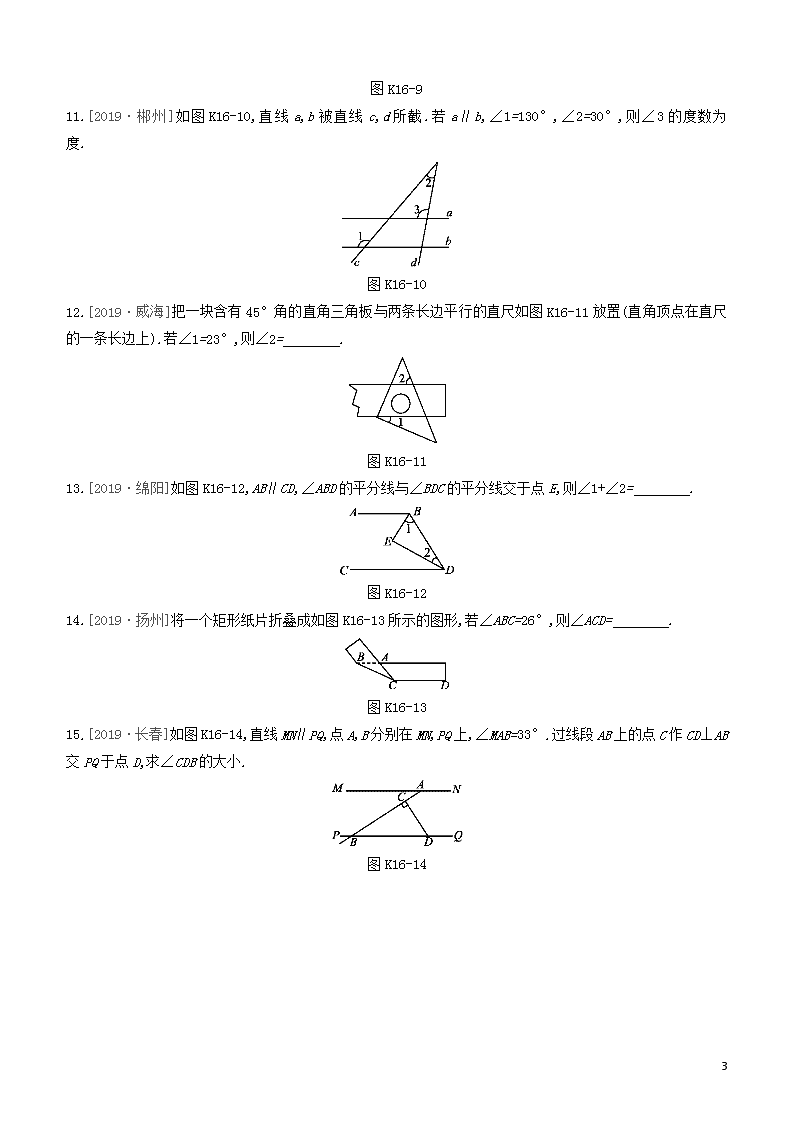‎ 8‎ 图K16-9‎ ‎11.[2019·郴州]如图K16-10,直线a,b被直线c,d所截.若a∥b,∠1=130°,∠2=30°,则∠3的度数为　　　　度. ‎ 图K16-10‎ ‎12.[2019·威海]把一块含有45°角的直角三角板与两条长边平行的直尺如图K16-11放置(直角顶点在直尺的一条长边上).若∠1=23°,则∠2=　　　　. ‎ 图K16-11‎ ‎13.[2019·绵阳]如图K16-12,AB∥CD,∠ABD的平分线与∠BDC的平分线交于点E,则∠1+∠2=　　　　. ‎ 图K16-12‎ ‎14.[2019·扬州]将一个矩形纸片折叠成如图K16-13所示的图形,若∠ABC=26°,则∠ACD=　　　　. ‎ 图K16-13‎ ‎15.[2019·长春]如图K16-14,直线MN∥PQ,点A,B分别在MN,PQ上,∠MAB=33°.过线段AB上的点C作CD⊥AB交PQ于点D,求∠CDB的大小.‎ 图K16-14‎ 8‎ ‎16.[2019·兰州]如图K16-15,AB=DE,BF=EC,∠B=∠E,求证:AC∥DF.‎ 图K16-15‎ ‎17.[2018·益阳]如图K16-16,AB∥CD,∠1=∠2,求证:AM∥CN.‎ 图K16-16‎ 8‎ ‎|拓展提升|‎ ‎18.[2019·淄博]如图K16-17,小明从A处出发沿北偏东40°方向行走至B处,又从点B处沿东偏南20°方向行走至C处,则∠ABC等于 (　　)‎ 图K16-17‎ A.130° B.120°‎ C.110° D.100°‎ ‎19.[2019·菏泽]如图K16-18,AD∥CE,∠ABC=100°,则∠2-∠1的度数是　　　　. ‎ 图K16-18‎ ‎20.[2018·北京]如图K16-19所示的网格是正方形网格,∠BAC　　　　∠DAE.(填“>”“=”或“<”) ‎ 图K16-19‎ 8‎ ‎【参考答案】‎ ‎1.B ‎2.D　[解析]∵∠ACD=∠A+∠B=30°+75°=105°,BD∥EF,∴∠E=∠ACD=105°,故选D.‎ ‎3.A　[解析]由题意知∠E=45°,∠B=30°,‎ ‎∵DE∥CB,‎ ‎∴∠BCF=∠E=45°,‎ 在△CFB中,∠BFC=180°-∠B-∠BCF=180°-30°-45°=105°.‎ 故选:A.‎ ‎4.C　[解析]如图,过点A作l3∥l1,将题中∠2分为∠4和∠5.‎ ‎∵l1∥l2,∴l2∥l3,‎ ‎∴∠4=∠1=30°,∠5+∠3=180°,‎ ‎∴∠2+∠3=∠4+∠5+∠3=210°.‎ 故选C.‎ ‎5.C　[解析] △ABC中,AB=AC,∠A=30°,‎ ‎∴∠ABC=75°,‎ ‎∵∠1=145°,∴∠FDB=35°.‎ 过点B作BG∥a,‎ ‎∵a∥b,∴BG∥b,‎ ‎∴∠FDB=∠DBG,∠2=∠CBG.‎ ‎∵∠ABC=∠ABG+∠CBG,‎ ‎∴∠2=75°-35°=40°.故选C.‎ ‎6.C　[解析]根据直线a∥b,两直线平行,同旁内角互补,可得∠2+∠BAC+∠1+∠BCA=180°,∴∠2=180°-∠BAC-∠1-∠BCA=180°-30°-90°-20°=40°,故选C.‎ ‎7.A　[解析]∵BA∥EF,‎ ‎∴∠OCF=∠A=30°.‎ ‎∴∠AOF=∠F+∠OCF=45°+30°=75°.‎ 故选A.‎ ‎8.B　[解析]∵钟面分成12等份,每一份中的弧的度数是30°,‎ ‎∴钟表上10点整时,时针与分针所成的角是60°.故选:B.‎ 8‎ ‎9.5　[解析]∵PB⊥l,PB=5 cm,‎ ‎∴P到l的距离是垂线段PB的长度5 cm,故答案为:5.‎ ‎10.∠1=∠3‎ ‎11.100　[解析]∵a∥b,‎ ‎∴∠1=∠2+∠3,‎ 又∵∠2=30°,‎ ‎∴∠3=∠1-∠2=130°-30°=100°,因此本题应填100.‎ ‎12.68°‎ ‎13.90°　[解析]∵AB∥CD,‎ ‎∴∠ABD+∠CDB=180°,‎ ‎∵BE是∠ABD的平分线,‎ ‎∴∠1=‎1‎‎2‎∠ABD,‎ ‎∵DE是∠BDC的平分线,‎ ‎∴∠2=‎1‎‎2‎∠CDB,‎ ‎∴∠1+∠2=90°,‎ 故答案为:90°.‎ ‎14.128°　[解析]延长DC,由题意可得:∠ABC=∠BCE=∠BCA=26°,则∠ACD=180°-26°-26°=128°.‎ 故答案为:128°.‎ ‎15.解:∵直线MN∥PQ,‎ ‎∴∠MAB=∠ABD=33°,‎ ‎∵CD⊥AB,∴∠BCD=90°,‎ ‎∴∠CDB=90°-33°=57°.‎ ‎16.证明:∵BF=EC,‎ ‎∴BF+FC=EC+FC,即BC=EF.‎ 又∵AB=DE,∠B=∠E,‎ ‎∴△ABC≌△DEF,‎ ‎∴∠ACB=∠DFE,‎ ‎∴AC∥DF.‎ ‎17.证明:∵AB∥CD,‎ ‎∴∠EAB=∠ACD.‎ ‎∵∠1=∠2,‎ ‎∴∠EAB-∠1=∠ACD-∠2,‎ 即∠EAM=∠ACN,‎ 8‎ ‎∴AM∥CN.‎ ‎18.C　[解析]如图,由题意,得∠DAB=40°,∠EBC=20°,‎ ‎∵南北方向上的两条直线是平行的,‎ ‎∴AD∥BF,∴∠ABF=∠DAB=40°.‎ 又∵∠EBF=90°,‎ ‎∴∠CBF=90°-20°=70°,‎ ‎∴∠ABC=∠ABF+∠CBF=40°+70°=110°.‎ ‎19.80°　[解析]作BF∥AD,‎ ‎∵AD∥CE,∴AD∥BF∥EC,‎ ‎∴∠1=∠3,∠4+∠2=180°,∠3+∠4=100°,‎ ‎∴∠1+∠4=100°,∠2+∠4=180°,‎ ‎∴∠2-∠1=80°.‎ ‎20.>‎ 8‎