第6章一次函数 题型专项训练-苏科版八年级数学上册期末复习 18页

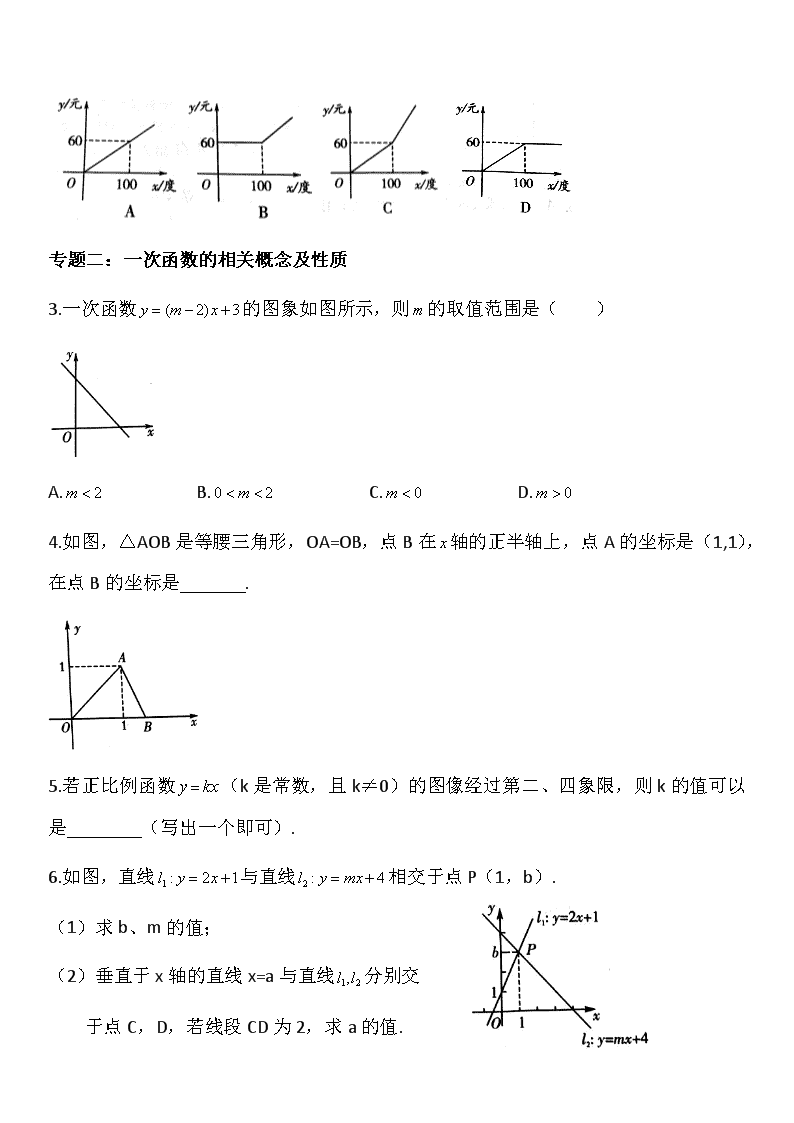
苏科版八年级上册期末复习训练 6：一次函数 知识导图： 专题一：函数的概念及图像 1.函数 1 1  xy 中，自变量 x 的取值范围是（ ） A. 0x B. 0x C. 1x D. 1x 2.为了节能减排，居民节约用电，某市出台了新的居民用电收费标准：（1）若每户居民 每月用电量不超过 100 度，则按 0.60 元/度计算；（2）若每户居民每月用电量超过 100 度，则超过部分按 0.8 元/度计算（未超过的部分仍按 0.60 元/度计算），现假设某用户 居民某月用电量是 x（单位：度），电费为 y（单位：元），则 y 与 x 的函数关系用图像 表示正确的是（ ） 专题二：一次函数的相关概念及性质 3.一次函数 3)2(  xmy 的图象如图所示，则 m 的取值范围是（ ） A. 2m B. 20  m C. 0m D. 0m 4.如图，△AOB 是等腰三角形，OA=OB，点 B 在 x 轴的正半轴上，点 A 的坐标是（1,1）， 在点 B 的坐标是 . 5.若正比例函数 kxy  （k 是常数，且 k≠0）的图像经过第二、四象限，则 k 的值可以 是 （写出一个即可）. 6.如图，直线 12:1  xyl 与直线 4:2  mxyl 相交于点 P（1，b）. （1）求 b、m 的值； （2）垂直于 x 轴的直线 x=a 与直线 21,ll 分别交 于点 C，D，若线段 CD 为 2，求 a 的值. 专题三：一次函数与一元一次方程、二元一次方程（组）、一元一次不等式（组）之间 的关系 7.如图，函数 32 21  axyxy 与 的图像相交于点 A )2,(m ，则关于 x 的不等式 32  axx 的 解集是（ ） A. 2x B. 2x C. 1x D. 1x 8.已知甲、乙两个函数图像上部分的横坐标 x 与对应的纵坐标 y 分别如表所示，两个函 数图像仅有一个交点，则这个交点的纵坐标 y 是（ ） 甲 乙 A. 0 B. 1 C. 2 D.3 专题四：一次函数的实际应用问题 9.小高从家门口骑车去单位上班，先走平路到达点 A，再走上坡路到达点 B，最后走下 坡路到达工作单位，所用的时间与路程的关系如图所示.下班后，如果他沿原路返回， 且走平路、上坡路、下坡路的速度分别保持和去上班时一致，那么他从单位到家门口 需要的时间是 分钟. 10.某市推出电脑上网包月制，每月收取费用 y（元）与上网时间 x（小时）的函数关系 如图所示，其中 BA 是线段，BA∥x 轴，AC 是射线. （1）当 x≥30，求 y 与 x 之间的函数关系式. （2）若小李 4 月份上网 20 小时，他应付多少元的上网费用？ （3）若小李 5 月份上网费用为 75 元，则他在该月份的上网时间是多少？ 11.某蓝莓种植生产基地产销两旺，采摘的蓝莓部分加工销售，部分直接销售，且当天 都能销售完，直接销售是 40 元/斤，加工销售是 130 元/斤（不计损耗）.已知基地雇用 20 名工人，每名工人只能参与采摘和加工中的一项工作，每人每天可以采摘 70 斤或加 工 35 斤.设安排 x 名工人采摘蓝莓，剩下的工人加工蓝莓. （1）若基地一天的总销售收入为 y 元，求 y 与 x 的函数关系式； （2）试求如何分配工人，才能使一天的销售收入最大？并求出最大值. 随堂练习 12.下列曲线中不能表示 y 是 x 的函数的是（ ） 13.一次函数 bkxy  满足 0kb ，且 y 随 x 的增大而减小，则此函数的图像不经过（ ）. A.第一象限 B.第二象限 C.第三象限 D.第四象限 14.同一温度的华氏度 y（°F）与摄氏度 x（°C）之间的函数表达式是 325 9  xy .若 某一温度的摄氏度数与华氏度数值恰好相等，则此温度的摄氏度为 °C. 15.如图，直线 AB： bxy  分别与 yx、 轴交于 A（6,0）、B 两点，过点 B 的直线交 x 轴 的负半轴于点 C，且 OB：OC=3:1. （1）求点 B 的坐标； （2）求直线 BC 的函数关系式； （3）若点 P（m，2）在△ABC 的内部，求 m 的取值范围. 16.小强与小刚都住在安康小区，在同一所学校读书，某天早上，小强 7:30 从安康小区 站乘坐校车去学校，途中需停靠两个站点才能到达学校站点，且每个站点停留 2 分钟， 校车行驶途中始终保持匀速，当天早上，小刚 7:39 从安康小区站乘坐出租车沿相同路 线出发，出租车匀速行驶，比小强乘坐的校车早 1 分钟到学校站点，他们乘坐的车辆 从安康小区站出发所行驶路程 y（千米）与校车行驶时间 x（分钟）之间的函数图像如 图所示. （1）求点 A 的纵坐标 m 的值； （2）小刚乘坐出租车出发后经过多少分钟追到小强乘坐的校车？并求此时他们距学校 站点的路程. 专项提优特训：融会贯通一次函数 一次函数拥有丰富的题型，例如：分段函数，自变量在不同的取值范围内，其表达 式（或图像）也是不同的；最大（小）值，与一元一次不等式（组）相互作用求得多 种方案或最值；存在问题，与等腰三角形或直角三角形联合使用确定图形点的坐标； 一次函数与图形变换等. 分类训练 类型一：分段函数的应用 1.某公司开发出一款新的节能产品，该产品的成本为 6 元/件，该产品正式投放市场前 通过代销点进行了为期一个月（30 天）的试销售，售价为 8 元/件，工作人员对销售情 况进行了跟踪记录，并将记录情况绘成图像，图中的折线 ODE 表示销售量 y（件）与 销售时间 x（天）之间的函数关系，已知线段 DE 表示函数关系中，时间每增加 1 天， 日销售量减少 5 件. （1）第 24 天的日销售量是 件，日销售利润是 元. （2）求 y 与 x 之间的函数表达式，并写出 x 的其值范围. （3）日销售利润不低于 640 元的天数有多少天试销售期间，日销售最大利润是多少元？ 2.如图①，某物流公司恰好位于连接 A、B 两地的一条公路旁的 C 处，某一天，该公司 同时派出甲、乙两辆货车以各自的速度匀速行驶.其中，甲车从公司出发直达 B 地，乙 车从公司出发开往 A 地，并在 A 地用 1h 配货，然后掉头按原始开往 B 地.图②是甲、 乙两地之间的距离 s（km）与它们出发后的时间 x（h）之间函数关系的部分图象. （1）由图象可知，甲车速度为 km/h；乙车速度为 km/h;乙车速度为 Km/h. （2）已知最终乙车比甲车早到 B 地 0.5h，求甲车出发 1.5h 后直至到达 B 地的过程中， s 与 x 的函数的取值范围，并在图②中补全函数图象. 3.端午节期间，甲、乙两人沿同一路线行驶，各自开车同时去离家 560 千米的景区游玩， 甲先以每小时 60 千米的速度匀速行驶 1 小时，再以每小时 m 千米的速度匀速行驶 1 小时，再以每小时 m 千米的速度行驶，途中休息了一段时间后，仍按每小时 m 千米的 速度匀速行驶，两人同时到达目的地，图中折线、线段分别表示甲、乙两人所走的路 程 )(),( kmykmy 乙甲 与时间 )(hx 之间的函数关系式他图像.请根据图像提供的信息，解决下列 问题： （1）图中 E 点的坐标是 ，题中 m= km/h，甲在途中休息 h； （2）求线段 CD 的表达式，并写出自变量 x 的取值范围； （3）两人第二次相遇后，又经过多长时间两人相距 20km？ 类型二：一次函数中方案问题 4.某书店现有资金 7700 元，计划全部用于购进甲、乙、丙三种图书共 20 套，其中甲种 图书每套 500 元，乙种图书每套 400 元，丙种图书每套 250 元.书店将甲、乙、丙三种 图书的售价分别定为每套 550 元，430 元，310 元.设书店购进甲种图书 x 套，乙种图书 y 套，请解答下列问题： （1）请求出 y 与 x 的函数表达式（不需要写出自变量的取值范围）. （2）若书店购进甲、乙两种图书均不少于 1 套，则该书店有几种进货方案？ （3）在（1）和（2）的条件下，根据市场调查，书店决定将三种图书的售价作出如下 调整：甲种图书的售价不变，乙种图书的售价上调 a（a 为整数）元，丙种图书的售价 下调 a 元，这样三种图书全部售出后，所获得的利润比（2）中某方案的利润多出 20 元，请直接写出书店是按哪种方案进的货及 a 的值. 5.某网店销售甲、乙两种防雾霾口罩 ，已知甲种口罩每袋的售价比乙种口罩多 5 元， 小丽从该网店网购 2 袋甲种口罩和 3 袋乙种口罩共花费 110 元. （1）该网店甲、乙两种口罩每袋的售价各是多少元？ （2）根据消费者需求，网店决定用不超过 10000 元购进甲、乙两种口罩共 500 袋，且 甲种口罩的数量大于乙种口罩的 5 4 ，已知甲种口罩每袋的进价为 22.4 元，乙种口罩每 袋的进价为 18 元，请你帮助网店计算有几种进货方法.若使网店获利最大，应该购进甲、 乙两种口罩各多少袋，最大获利多少元？ 类型三：一次函数与图形结合考查 6.如图，在平面直角坐标系中，函数 xy 2 和 xy  的图像分别为直线 21,ll ，过点（1,0） 作 x 轴的垂线交 1l 于点 1A ，过点 1A 作 y 轴的垂线交 2l 于点 2A ，过点 2A 作 x 轴的垂线交 1l 于 点 3A 作 y 轴的垂线交 2l 于点 4A ......依次进行下去，则点 2021A 的坐标为 . 7.如图，在平面直角坐标系 xOy 中，已知正比例函数 xy 3 4 与一次函数 7 xy 的图像 交于点 A. （1）求点 A 的坐标； （2）在 y 轴上确定点 M，使得△AOM 是等腰三角形，请求出点 M 的坐标； （3）如图，设 x 轴上一点 P（a，1），过点 P 作 x 轴的垂线（垂线位于点 A 的右侧）， 分别交 xy 3 4 和 7 xy 的图像于点 B，C，连接 OC，若 BC= 5 14 OA，求△ABC 的面积及 点 B，C 的坐标； （4）在（3）的条件下，设直线 7 xy 交 x 轴于点 D，在直线 BC 上确定点 E，使得△ ADE 的周长最小，请求出点 E 的坐标. 参考答案 1. D 2. C 3. A 4. （ 02，） 5. -2 6.（1）∵点 P（1，b）在直线 12:1  xyl 上， ∴ 3112 b ∵点 P（1,3）在直线 42  mxl 上， ∴3=m+4 解得 m=-1. （2）当 x=a 时， 12  ayc ； 当 ax  时， .4 ayD  ； ∵CD=2， ∴ 2|)4(12|  aa . 解得 3 1a 或 3 5a . 7.D 8.D 9.15 10.（1）当 30x 时，设函数关系式为 bkxy  ， 则      9040 6030 bk bk ，解得      30 3 b k . 所以 303  xy . （2）4 月份上网 20 小时，应付上网费 60 元. （3）由 75=3x-30，解得 x=35. 所以 5 月份网 35 个小时. 11.（1）根据题意，得 ]35)20(70[  xxy ×40+ 6300035013035)20(  xx . （2）∵ ),20(3570 xx  ∴ 3 20x ∵ x 为正整数，且 20x ， ∴ 207  x . ∵ 63000350  xy 中， 0350 k ∴y 随 x 值的增大而减少， ∴当 x=7 时，y 取最大值， 最大值为-350×7+63000=60550. 故安排 7 名工人采摘，13 名工人进行加工，才能使一天的收入最大，最大收入为 60550 元. 12. C 13. A 14. -40 15. （1）将点 A（6,0）带入直线 AB 的函数表达式， 得 0=-6-b，解得 b=-6. ∴直线 AB 的解析式为 6 xy ∴点 B 的坐标为（0，6）. （2）∵OB：OC=3:1，B（0,6）， ∴OC=2， ∴点 C 的坐标为（-2,0） 设 BC 的函数关系式是 6 kxy ， 令 0=-2k+6，解得 k=3， ∴直线 BC 的函数关系是 63  xy ， （3）把 2y 代入 6 xy 得 .4x 把 2y 代入 63  xy ，得 3 4x . 结合图象可知 m 的取值范围是 43 4  m . 16.（1）∵校车的数为 3÷4=0.75（千米/分钟） ∴点 A 的纵坐标 m=3+0.75×（8-6）=4.5. 故点 A 的纵坐标 m 的值为 4.5. （2）校车到达学校站点所需时间为 9÷0.75+4=16（分钟）， ∴出租车的速度为 9÷6=1.5（千米/分钟） ∴两车相遇时出租车出发时间为 0.75×（9-4）÷（1.5-0.75）=5（分钟）. ∴相遇地点离学校站点的路程为 9-1.5×5=1.5（千米）. 故小刚乘坐出租车出发后经过 5 分钟追到到小强所乘坐的校车，此时他们距学校站点 的路程为 1.5 千米. 专项提优训练： 1.（1）330 660 （2）y 与 x 之间的函数关系是为      )3018(4505 )180(20 xx xxy （3）有 11 天，最大利润为 720 元. 2.（1）40 80 （2）        )55.4(20040 )5.44(16040 )45.1(16040 xx xx xx S 补全函数图像如图所所示. 3.（1）（2，160） 100 1 （2） 36060)14(100  ∴B（4,360）， ∴C（5,360），D（7,560）代入，得      5607 3605 bk bk 解得      140 100 b k ∴线段 CD 的表达式为 )75(140100  xxy （3）①当 4.55 时，80x-（100x-140）=20，x=6，6-4.5=1.5（h） 答：两人第二次相遇后，又经过 0.25 小时或 1.5 小时两人相距 20km. 4.（1）函数表达式为 183 5  xy . （2）根据题意的 5 1101183 5  xx ，解得 又∵x≥1，∴1≤x≤ 5 110 ∵x≥1，∴ 5 1101  x ∵ )20(,, yxyx  为整数，∴x=3,6,9 即有三种进货方案： ①甲、乙、丙三种图书分别为 3 套，13 套，4 套， ②甲、乙、丙三种图书分别为 6 套，8 套，6 套， ③甲、乙、丙三种图书分别为 9 套，3 套，8 套. （3）若按方案一，则有 20413  aa ，解得： 9 20a （舍） 若按方案二，则有 2068  aa ，解得： 10a （符合题意） 若按方案三，则有 2083  aa ，解得 4a （舍） 所以进货方法是甲、乙、丙三种图书分别为 6 套，8 套，6 套，a=10 5.（1）设该网店甲种口罩每袋零售价为 x 元，乙种口罩每袋的零售价为 y 元，根据题 意得      11032 5 yx yx ，解得      20 25 y x ，故该网店甲种口罩每袋的售价为 25 元，乙种口罩每袋 的售价为 20 元. （2）设该网店购进甲种口罩 m 袋，购进乙种口罩（500-m）袋，根据题意得：      10000)500(184.22 ),500(5 4 mm mm 解这个不等式组得 11 32279 2222  m . 因为 m 为整数，故有 5 种进货方案，分别是：购进甲种口罩 223 袋，乙种口罩 277 袋； 购进甲种口罩 224 袋，乙种口罩 276 袋；购进甲种口罩 225 袋，乙种口罩 275 袋； 购进甲种口罩 226 袋，乙种口罩 274 袋；购进甲种口罩 227 袋，乙种口罩 273 袋； 当购进甲种口罩 227 袋，乙种口罩 273 袋获利最大，最大利润为 1136.2 元. 6.（ 10111010 22 ， ） 7.（1）A 的坐标为（3,4） （2）根据勾股定理，得 OA=5， 如图①所示，分四种情况考虑，当 51  OAOM 时， );5,0(1M 当 52  OAOM 时， )5,0(2 M ； 当 53  OAAM 时， )8,0(3M ；当 44 AMOM  时， )8 25,0(4M .综上所述，点 M 的坐标为 )8 25,0()8,0()5,0()5,0( 或、、  （3）设点 B )7,(),3 4,( aaCaa ，∵BC OA5 14 = 55 14  =14， ∴ 14)7(3 4  aa ，解得 9a ，过点 A 作 AQ⊥BC 于点 Q，如图②所示， ∴ 42)39(142 1 2 1  AQBCS ABC ，当 a=9 时， 1293 4 3 4 a ， 2797  a ， 点 B（9,12），C（9，-2）. （4）如图③所示，作 D 关于直线 BC 的对称点 D′，连接 AD′，与直线 BC 交于点 E， 连接 DE，此时△ADE 的周长最小. 对于直线 7 xy ，令 0y ，得 7x ，即 )0,7(D ，由（3）得直线 BC 为直线 9x ， ∴D′（11,0）.设直线 AD′的表达式为 bkxy  ，把 A 与 D′的坐标带入，得      011 43 bk bk ， 解得        2 11 2 1 b k 所以直线 AD′的表达式为 2 11 2 1  xy .令 9x ，得 1y ，则此时点 E 的坐标为（9,1）.