2018年山东省泰安市中考数学试卷含答案 22页

‎2018年山东省泰安市中考数学试卷 ‎　‎ 一、选择题（本大题共12小题，在每小题给出的四个选项中，只有一个是正确的，请把正确的选项选出来，每小题选对得3分，选错、不选或选出的答案超过一个，均记零分）‎ ‎1．（3分）计算：﹣（﹣2）+（﹣2）0的结果是（　　）‎ A．﹣3 B．0 C．﹣1 D．3‎ ‎2．（3分）下列运算正确的是（　　）‎ A．2y3+y3=3y6 B．y2•y3=y6 C．（3y2）3=9y6 D．y3÷y﹣2=y5‎ ‎3．（3分）如图是下列哪个几何体的主视图与俯视图（　　）‎ A． B． C． D．‎ ‎4．（3分）如图，将一张含有30°角的三角形纸片的两个顶点叠放在矩形的两条对边上，若∠2=44°，则∠1的大小为（　　）‎ A．14° B．16° C．90°﹣α D．α﹣44°‎ 22‎ ‎5．（3分）某中学九年级二班六组的8名同学在一次排球垫球测试中的成绩如下（单位：个）‎ ‎35 38 42 44 40 47 45 45‎ 则这组数据的中位数、平均数分别是（　　）‎ A．42、42 B．43、42 C．43、43 D．44、43‎ ‎6．（3分）夏季来临，某超市试销A、B两种型号的风扇，两周内共销售30台，销售收入5300元，A型风扇每台200元，B型风扇每台150元，问A、B两种型号的风扇分别销售了多少台？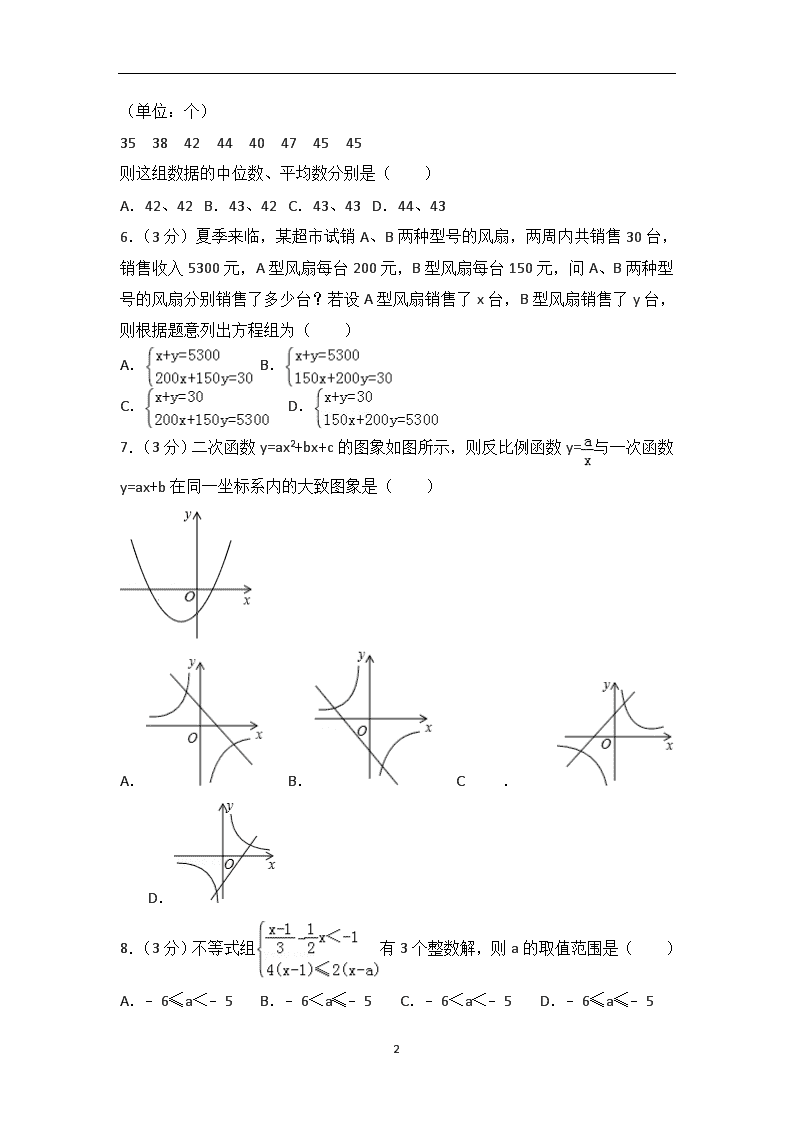若设A型风扇销售了x台，B型风扇销售了y台，则根据题意列出方程组为（　　）‎ A． B．‎ C． D．‎ ‎7．（3分）二次函数y=ax2+bx+c的图象如图所示，则反比例函数y=与一次函数y=ax+b在同一坐标系内的大致图象是（　　）‎ A． B． C． D．‎ ‎8．（3分）不等式组有3个整数解，则a的取值范围是（　　）‎ A．﹣6≤a＜﹣5 B．﹣6＜a≤﹣5 C．﹣6＜a＜﹣5 D．﹣6≤a≤﹣5‎ 22‎ ‎9．（3分）如图，BM与⊙O相切于点B，若∠MBA=140°，则∠ACB的度数为（　　）‎ A．40° B．50° C．60° D．70°‎ ‎10．（3分）一元二次方程（x+1）（x﹣3）=2x﹣5根的情况是（　　）‎ A．无实数根 B．有一个正根，一个负根 C．有两个正根，且都小于3 D．有两个正根，且有一根大于3‎ ‎11．（3分）如图，将正方形网格放置在平面直角坐标系中，其中每个小正方形的边长均为1，△ABC经过平移后得到△A1B1C1，若AC上一点P（1.2，1.4）平移后对应点为P1，点P1绕原点顺时针旋转180°，对应点为P2，则点P2的坐标为（　　）‎ A．（2.8，3.6） B．（﹣2.8，﹣3.6） C．（3.8，2.6） D．（﹣3.8，﹣2.6）‎ ‎12．（3分）如图，⊙M的半径为2，圆心M的坐标为（3，4），点P是⊙M上的任意一点，PA⊥PB，且PA、PB与x轴分别交于A、B两点，若点A、点B关于原点O对称，则AB的最小值为（　　）‎ 22‎ A．3 B．4 C．6 D．8‎ ‎　‎ 二、填空题（本大题共6小题，满分18分。只要求填写最后结果，每小题填对得3分)‎ ‎13．（3分）一个铁原子的质量是0.000000000000000000000000093kg，将这个数据用科学记数法表示为　 　kg．‎ ‎14．（3分）如图，⊙O是△ABC的外接圆，∠A=45°，BC=4，则⊙O的直径为　 　．‎ ‎15．（3分）如图，在矩形ABCD中，AB=6，BC=10，将矩形ABCD沿BE折叠，点A落在A'处，若EA'的延长线恰好过点C，则sin∠ABE的值为　 　．‎ ‎16．（3分）观察“田”字中各数之间的关系：‎ 则c的值为　 　．‎ ‎17．（3分）如图，在△ABC中，AC=6，BC=10，tanC=，点D是AC边上的动点（不与点C重合），过D作DE⊥BC，垂足为E，点F是BD的中点，连接EF，设CD=x，△DEF的面积为S，则S与x之间的函数关系式为　 　．‎ 22‎ ‎18．（3分）《九章算术》是中国传统数学最重要的著作，在“勾股”章中有这样一个问题：“今有邑方二百步，各中开门，出东门十五步有木，问：出南门几步面见木？”‎ 用今天的话说，大意是：如图，DEFG是一座边长为200步（“步”是古代的长度单位）的正方形小城，东门H位于GD的中点，南门K位于ED的中点，出东门15步的A处有一树木，求出南门多少步恰好看到位于A处的树木（即点D在直线AC上）？请你计算KC的长为　 　步．‎ ‎　‎ 三、解答题（本大题共7小题，满分66分。解答应写出必要的文字说明、证明过程或推演步骤)‎ ‎19．（6分）先化简，再求值÷（﹣m﹣1），其中m=﹣2‎ ‎20．（9分）文美书店决定用不多于20000元购进甲乙两种图书共1200本进行销售．甲、乙两种图书的进价分别为每本20元、14元，甲种图书每本的售价是乙种图书每本售价的1.4倍，若用1680元在文美书店可购买甲种图书的本数比用1400元购买乙种图书的本数少10本．‎ ‎（1）甲乙两种图书的售价分别为每本多少元？‎ ‎（2）书店为了让利读者，决定甲种图书售价每本降低3元，乙种图书售价每本降低2元，问书店应如何进货才能获得最大利润？（购进的两种图书全部销售完．）‎ 22‎ ‎21．（8分）为增强学生的安全意识，我市某中学组织初三年级1000名学生参加了“校园安全知识竞赛”，随机抽取一个班学生的成绩进行整理，分为A，B，C，D四个等级，并把结果整理绘制成条形统计图与扇形统计图（部分），请依据如图提供的信息，完成下列问题：‎ ‎（1）请估计本校初三年级等级为A的学生人数；‎ ‎（2）学校决定从得满分的3名女生和2名男生中随机抽取3人参加市级比赛，请求出恰好抽到2名女生和1名男生的概率．‎ ‎22．（9分）如图，矩形ABCD的两边AD、AB的长分别为3、8，E是DC的中点，反比例函数y=的图象经过点E，与AB交于点F．‎ ‎（1）若点B坐标为（﹣6，0），求m的值及图象经过A、E两点的一次函数的表达式；‎ ‎（2）若AF﹣AE=2，求反比例函数的表达式．‎ ‎23．（11分）如图，△ABC中，D是AB上一点，DE⊥AC于点E，F是AD的中点，FG⊥BC于点G，与DE交于点H，若FG=AF，AG平分∠CAB，连接GE，CD．‎ ‎（1）求证：△ECG≌△GHD；‎ ‎（2）小亮同学经过探究发现：AD=AC+EC．请你帮助小亮同学证明这一结论．‎ 22‎ ‎（3）若∠B=30°，判定四边形AEGF是否为菱形，并说明理由．‎ ‎24．（11分）如图，在平面直角坐标系中，二次函数y=ax2+bx+c交x轴于点A（﹣4，0）、B（2，0），交y轴于点C（0，6），在y轴上有一点E（0，﹣2），连接AE．‎ ‎（1）求二次函数的表达式；‎ ‎（2）若点D为抛物线在x轴负半轴上方的一个动点，求△ADE面积的最大值；‎ ‎（3）抛物线对称轴上是否存在点P，使△AEP为等腰三角形？若存在，请直接写出所有P点的坐标，若不存在请说明理由．‎ ‎25．（12分）如图，在菱形ABCD中，AC与BD交于点O，E是BD上一点，EF∥AB，∠EAB=∠EBA，过点B作DA的垂线，交DA的延长线于点G．‎ ‎（1）∠DEF和∠AEF是否相等？若相等，请证明；若不相等，请说明理由；‎ ‎（2）找出图中与△AGB相似的三角形，并证明；‎ ‎（3）BF的延长线交CD的延长线于点H，交AC于点M．求证：BM2=MF•MH．‎ 22‎ ‎　‎ 22‎ ‎2018年山东省泰安市中考数学试卷 参考答案与试题解析 ‎　‎ 一、选择题（本大题共12小题，在每小题给出的四个选项中，只有一个是正确的，请把正确的选项选出来，每小题选对得3分，选错、不选或选出的答案超过一个，均记零分）‎ ‎1．‎ ‎【解答】解：﹣（﹣2）+（﹣2）0‎ ‎=2+1‎ ‎=3，‎ 故选：D．‎ ‎　‎ ‎2．‎ ‎【解答】解：2y3+y3=3y3，A错误；‎ y2•y3=y5，B错误；‎ ‎（3y2）3=27y6，C错误；‎ y3÷y﹣2=y3﹣（﹣2）=y5，‎ 故选：D．‎ ‎　‎ ‎3．‎ ‎【解答】解：由已知主视图和俯视图可得到该几何体是圆柱体的一半，只有选项C符合题意．‎ 故选：C．‎ ‎　‎ ‎4．‎ ‎【解答】解：如图，∵矩形的对边平行，‎ ‎∴∠2=∠3=44°，‎ 22‎ 根据三角形外角性质，可得∠3=∠1+30°，‎ ‎∴∠1=44°﹣30°=14°，‎ 故选：A．‎ ‎　‎ ‎5．‎ ‎【解答】解：把这组数据排列顺序得：35 38 40 42 44 45 45 47，‎ 则这组数据的中位数为：=43，‎ ‎=（35+38+42+44+40+47+45+45）=42，‎ 故选：B．‎ ‎　‎ ‎6．‎ ‎【解答】解：设A型风扇销售了x台，B型风扇销售了y台，‎ 则根据题意列出方程组为：．‎ 故选：C．‎ ‎　‎ ‎7．‎ ‎【解答】解：由二次函数开口向上可得：a＞0，对称轴在y轴左侧，故a，b同号，则b＞0，‎ 故反比例函数y=图象分布在第一、三象限，一次函数y=ax+b经过第一、二、三象限．‎ 故选：C．‎ ‎　‎ ‎8．‎ 22‎ ‎【解答】解：不等式组，‎ 由﹣x＜﹣1，解得：x＞4，‎ 由4（x﹣1）≤2（x﹣a），解得：x≤2﹣a，‎ 故不等式组的解为：4＜x≤2﹣a，‎ 由关于x的不等式组有3个整数解，‎ 解得：7≤2﹣a＜8，‎ 解得：﹣6＜a≤﹣5．‎ 故选：B．‎ ‎　‎ ‎9．‎ ‎【解答】解：如图，连接OA、OB，‎ ‎∵BM是⊙O的切线，‎ ‎∴∠OBM=90°，‎ ‎∵∠MBA=140°，‎ ‎∴∠ABO=50°，‎ ‎∵OA=OB，‎ ‎∴∠ABO=∠BAO=50°，‎ ‎∴∠AOB=80°，‎ ‎∴∠ACB=∠AOB=40°，‎ 故选：A．‎ ‎　‎ 22‎ ‎10．‎ ‎【解答】解：（x+1）（x﹣3）=2x﹣5‎ 整理得：x2﹣2x﹣3=2x﹣5，‎ 则x2﹣4x+2=0，‎ ‎（x﹣2）2=2，‎ 解得：x1=2+＞3，x2=2﹣，‎ 故有两个正根，且有一根大于3．‎ 故选：D．‎ ‎　‎ ‎11．‎ ‎【解答】解：由题意将点P向下平移5个单位，再向左平移4个单位得到P1，‎ ‎∵P（1.2，1.4），‎ ‎∴P1（﹣2.8，﹣3.6），‎ ‎∵P1与P2关于原点对称，‎ ‎∴P2（2.8，3.6），‎ 故选：A．‎ ‎　‎ ‎12．‎ ‎【解答】解：∵PA⊥PB，‎ ‎∴∠APB=90°，‎ ‎∵AO=BO，‎ ‎∴AB=2PO，‎ 若要使AB取得最小值，则PO需取得最小值，‎ 连接OM，交⊙M于点P′，当点P位于P′位置时，OP′取得最小值，‎ 过点M作MQ⊥x轴于点Q，‎ 22‎ 则OQ=3、MQ=4，‎ ‎∴OM=5，‎ 又∵MP′=2，‎ ‎∴OP′=3，‎ ‎∴AB=2OP′=6，‎ 故选：C．‎ ‎　‎ 二、填空题（本大题共6小题，满分18分。只要求填写最后结果，每小题填对得3分)‎ ‎13．‎ ‎【解答】解：0.000000000000000000000000093=9.3×10﹣26，‎ 故答案为：9.3×10﹣26．‎ ‎　‎ ‎14．‎ ‎【解答】解：如图，连接OB，OC，‎ ‎∵∠A=45°，‎ ‎∴∠BOC=90°，‎ ‎∴△BOC是等腰直角三角形，‎ 又∵BC=4，‎ ‎∴BO=CO=BC•cos45°=2，‎ ‎∴⊙O的直径为4，‎ 故答案为：4．‎ 22‎ ‎　‎ ‎15．‎ ‎【解答】解：由折叠知，A'E=AE，A'B=AB=6，∠BA'E=90°，‎ ‎∴∠BA'C=90°，‎ 在Rt△A'CB中，A'C==8，‎ 设AE=x，则A'E=x，‎ ‎∴DE=10﹣x，CE=A'C+A'E=8+x，‎ 在Rt△CDE中，根据勾股定理得，（10﹣x）2+36=（8+x）2，‎ ‎∴x=2，‎ ‎∴AE=2，‎ 在Rt△ABE中，根据勾股定理得，BE==2，‎ ‎∴sin∠ABE==，‎ 故答案为：．‎ ‎　‎ ‎16．‎ ‎【解答】解：经过观察每个“田”左上角数字依此是1，3，5，7等奇数，此位置数为15时，恰好是第8个奇数，即此“田”字为第8个．观察每个“田”字左下角数据，可以发现，规律是2，22，23，24等，则第8 数为28．观察左下和右上角，每个“田”字的右上角数字依次比左下角大0，2，4，6等，到第8个图多14．则c=28+14=270‎ 故应填：270或28+14‎ ‎　‎ ‎17．‎ 22‎ ‎【解答】解：（1）在Rt△CDE中，tanC=，CD=x ‎∴DE=x，CE=x，‎ ‎∴BE=10﹣x，‎ ‎∴S△BED=×（10﹣x）•x=﹣x2+3x．‎ ‎∵DF=BF，‎ ‎∴S=S△BED=x2，‎ 故答案为S=x2．‎ ‎　‎ ‎18．‎ ‎【解答】解：DH=100，DK=100，AH=15，‎ ‎∵AH∥DK，‎ ‎∴∠CDK=∠A，‎ 而∠CKD=∠AHD，‎ ‎∴△CDK∽△DAH，‎ ‎∴=，即=，‎ ‎∴CK=．‎ 答：KC的长为步．‎ 故答案为．‎ ‎　‎ 三、解答题（本大题共7小题，满分66分。解答应写出必要的文字说明、证明过程或推演步骤)‎ 22‎ ‎19．‎ ‎【解答】解：原式=÷（﹣）‎ ‎=÷‎ ‎=•‎ ‎=﹣，‎ 当m=﹣2时，‎ 原式=﹣‎ ‎=﹣‎ ‎=﹣1+2．‎ ‎　‎ ‎20．‎ ‎【解答】解：（1）设乙种图书售价每本x元，则甲种图书售价为每本1.4x元 由题意得：‎ 解得：x=20‎ 经检验，x=20是原方程的解 ‎∴甲种图书售价为每本1.4×20=28元 答：甲种图书售价每本28元，乙种图书售价每本20元 ‎（2）设甲种图书进货a本，总利润元，则 ‎=（28﹣20﹣3）a+（20﹣14﹣2）（1200﹣a）=a+4800‎ ‎∵20a+14×（1200﹣a）≤20000‎ 解得a≤‎ ‎∵w随a的增大而增大 ‎∴当a最大时w最大 ‎∴当a=533本时，w最大 此时，乙种图书进货本数为1200﹣533=667（本）‎ 22‎ 答：甲种图书进货533本，乙种图书进货667本时利润最大．‎ ‎　‎ ‎21．‎ ‎【解答】解：（1）∵所抽取学生的总数为8÷20%=40人，‎ ‎∴该班级等级为A的学生人数为40﹣（25+8+2）=5人，‎ 则估计本校初三年级等级为A的学生人数为1000×=125人；‎ ‎（2）设两位满分的男生记为A1、A2、三位满分的女生记为B1、B2、B3，‎ 从这5名同学中选3人的所有等可能结果为：‎ ‎（B1，B2，B3）、（A2，B2，B3）、（A2，B1，B3）、（A2，B1，B2）、（A1，B2，B3）、‎ ‎（A1，B1，B3）、（A1，B1，B2）、（A1，A2，B3）、（A1，A2，B2）、（A1，A2，B1），‎ 其中恰好有2名女生、1名男生的结果有6种，‎ 所以恰好抽到2名女生和1名男生的概率为=．‎ ‎　‎ ‎22．‎ ‎【解答】解：（1）点B坐标为（﹣6，0），AD=3，AB=8，E为CD的中点，‎ ‎∴点A（﹣6，8），E（﹣3，4），‎ 函数图象经过E点，‎ ‎∴m=﹣3×4=﹣12，‎ 设AE的解析式为y=kx+b，‎ ‎，‎ 解得，‎ 一次函数的解析是为y=﹣x；‎ ‎（2）AD=3，DE=4，‎ ‎∴AE==5，‎ 22‎ ‎∵AF﹣AE=2，‎ ‎∴AF=7，‎ BF=1，‎ 设E点坐标为（a，4），则F点坐标为（a﹣3，1），‎ ‎∵E，F两点在函数y=图象上，‎ ‎∴4a=a﹣3，解得a=﹣1，‎ ‎∴E（﹣1，4），‎ ‎∴m=﹣1×4=﹣4，‎ ‎∴y=﹣．‎ ‎　‎ ‎23．‎ ‎【解答】解：（1）∵AF=FG，‎ ‎∴∠FAG=∠FGA，‎ ‎∵AG平分∠CAB，‎ ‎∴∠CAG=∠FGA，‎ ‎∴∠CAG=∠FGA，‎ ‎∴AC∥FG，‎ ‎∵DE⊥AC，‎ ‎∴FG⊥DE，‎ ‎∵FG⊥BC，‎ ‎∴DE∥BC，‎ ‎∴AC⊥BC，‎ ‎∴∠C=∠DHG=90°，∠CGE=∠GED，‎ ‎∵F是AD的中点，FG∥AE，‎ ‎∴H是ED的中点，‎ ‎∴FG是线段ED的垂直平分线，‎ ‎∴GE=GD，∠GDE=∠GED，‎ 22‎ ‎∴∠CGE=∠GDE，‎ ‎∴△ECG≌△GHD；‎ ‎（2）证明：过点G作GP⊥AB于P，‎ ‎∴GC=GP，而AG=AG，‎ ‎∴△CAG≌△PAG，‎ ‎∴AC=AP，‎ 由（1）可得EG=DG，‎ ‎∴Rt△ECG≌Rt△GPD，‎ ‎∴EC=PD，‎ ‎∴AD=AP+PD=AC+EC；‎ ‎（3）四边形AEGF是菱形，‎ 证明：∵∠B=30°，‎ ‎∴∠ADE=30°，‎ ‎∴AE=AD，‎ ‎∴AE=AF=FG，‎ 由（1）得AE∥FG，‎ ‎∴四边形AECF是平行四边形，‎ ‎∴四边形AEGF是菱形．‎ ‎　‎ ‎24．‎ ‎【解答】解：（1）∵二次函数y=ax2+bx+c经过点A（﹣4，0）、B（2，0），C（0，6），‎ ‎∴，‎ 22‎ 解得，，‎ 所以二次函数的解析式为：y=，‎ ‎（2）由A（﹣4，0），E（0，﹣2），可求AE所在直线解析式为y=，‎ 过点D作DN⊥x轴，交AE于点F，交x轴于点G，过点E作EH⊥DF，垂足为H，如图 设D（m，），则点F（m，），‎ ‎∴DF=﹣（）=，‎ ‎∴S△ADE=S△ADF+S△EDF=×DF×AG+DF×EH ‎=×DF×AG+×DF×EH ‎=×4×DF ‎=2×（）‎ ‎=，‎ ‎∴当m=时，△ADE的面积取得最大值为．‎ ‎（3）y=的对称轴为x=﹣1，‎ 设P（﹣1，n），又E（0，﹣2），A（﹣4，0），‎ 可求PA=，PE=，AE=，‎ 22‎ 当PA=PE时，=，‎ 解得，n=1，此时P（﹣1，1）；‎ 当PA=AE时，=，‎ 解得，n=，此时点P坐标为（﹣1，）；‎ 当PE=AE时，=，‎ 解得，n=﹣2，此时点P坐标为：（﹣1，﹣2）．‎ 综上所述，‎ P点的坐标为：（﹣1，1），（﹣1，），（﹣1，﹣2）．‎ ‎　‎ ‎25．‎ ‎【解答】解：（1）∠DEF=∠AEF，‎ 理由：∵EF∥AB，‎ ‎∴∠DEF=∠EBA，∠AEF=∠EAB，‎ ‎∵∠EAB=∠EBA，‎ ‎∴∠DEF=∠AEF；‎ ‎（2）△EOA∽△AGB，‎ 理由：∵四边形ABCD是菱形，‎ ‎∴AB=AD，AC⊥BD，‎ ‎∴∠GAB=∠ABE+∠ADB=2∠ABE，‎ ‎∵∠AEO=∠ABE+∠BAE=2∠ABE，‎ ‎∵∠GAB=∠AEO，∠GAB=∠AOE=90°，‎ ‎∴△EOA∽△AGB；‎ ‎（3）如图，连接DM，∵四边形ABCD是菱形，‎ 由对称性可知，BM=DM，∠ADM=∠ABM，‎ ‎∵AB∥CH，‎ 22‎ ‎∴∠ABM=∠H，‎ ‎∴∠ADM=∠H，‎ ‎∵∠DMH=∠FMD，‎ ‎∴△MFD∽△MDH，‎ ‎∴，‎ ‎∴DM2=MF•MH，‎ ‎∴BM2=MF•MH．‎ ‎　‎ 22‎