九年级上册数学周周测第二十三章 旋转周周测5（23-1—23-2） 人教版 4页

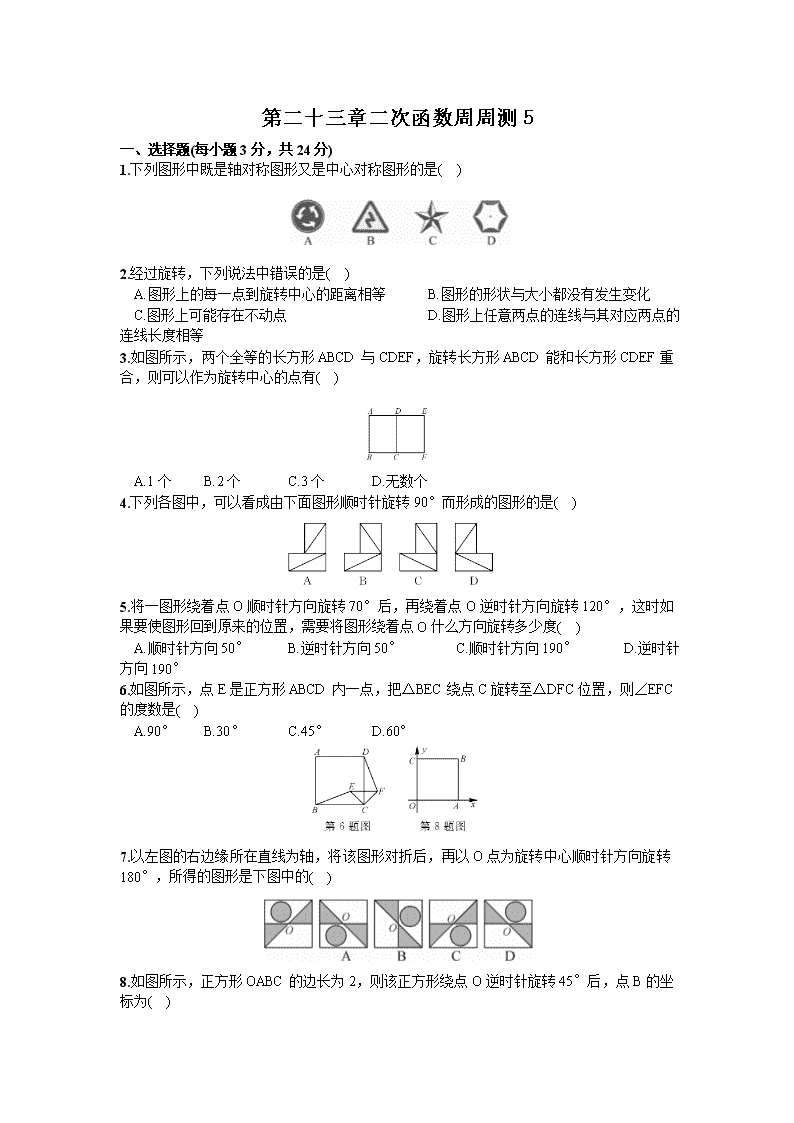
第二十三章二次函数周周测5‎ 一、选择题(每小题3分，共24分)‎ ‎1.下列图形中既是轴对称图形又是中心对称图形的是( )‎ ‎2.经过旋转，下列说法中错误的是( )‎ ‎ A.图形上的每一点到旋转中心的距离相等 B.图形的形状与大小都没有发生变化 ‎ C.图形上可能存在不动点 D.图形上任意两点的连线与其对应两点的连线长度相等 ‎3.如图所示，两个全等的长方形ABCD与CDEF，旋转长方形ABCD能和长方形CDEF重合，则可以作为旋转中心的点有( )‎ ‎ A.1个 B.2个 C.3个 D.无数个 ‎4.下列各图中，可以看成由下面图形顺时针旋转90°而形成的图形的是( )‎ ‎5.将一图形绕着点O顺时针方向旋转70°后，再绕着点O逆时针方向旋转120°，这时如果要使图形回到原来的位置，需要将图形绕着点O什么方向旋转多少度( )‎ ‎ A.顺时针方向50° B.逆时针方向50° C.顺时针方向190° D.逆时针方向190°‎ ‎6.如图所示，点E是正方形ABCD内一点，把△BEC绕点C旋转至△DFC位置，则∠EFC的度数是( )‎ ‎ A.90° B.30° C.45° D.60°‎ ‎7.以左图的右边缘所在直线为轴，将该图形对折后，再以O点为旋转中心顺时针方向旋转180°，所得的图形是下图中的( )‎ ‎8.如图所示，正方形OABC的边长为2，则该正方形绕点O逆时针旋转45°后，点B的坐标为( )‎ ‎ 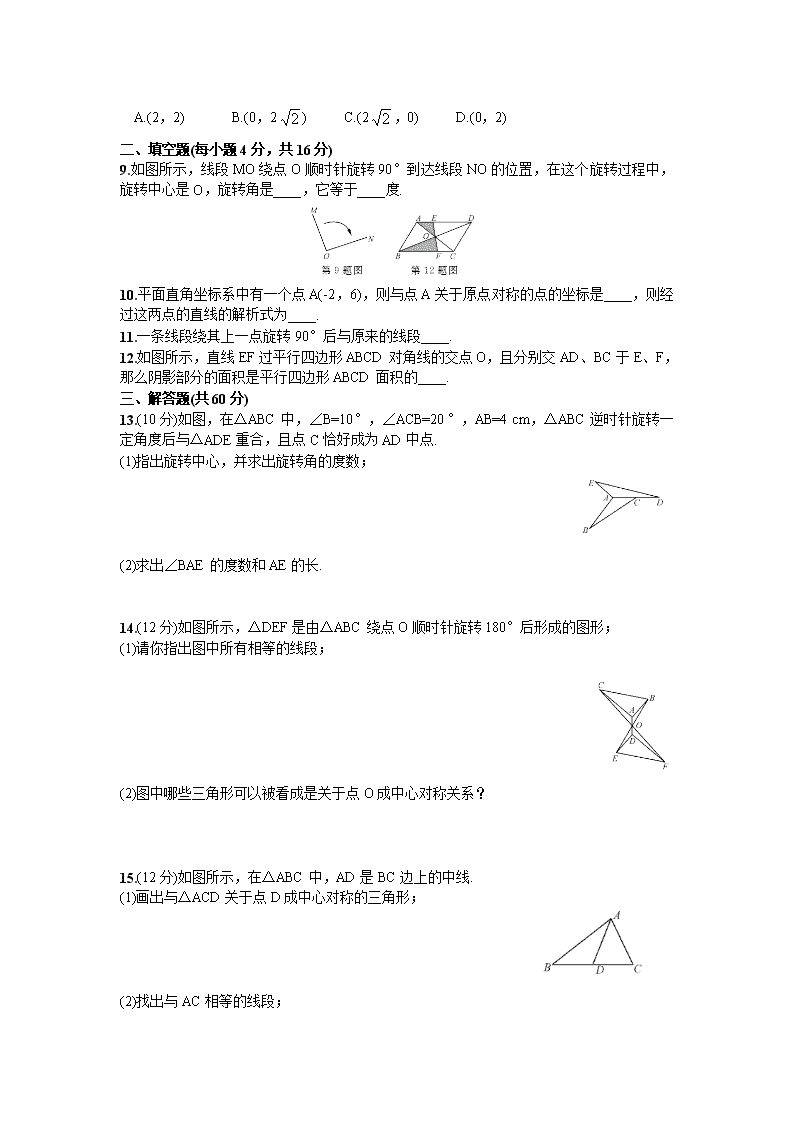A.(2，2) B.(0，2) C.(2，0) D.(0，2)‎ 二、填空题(每小题4分，共16分)‎ ‎9.如图所示，线段MO绕点O顺时针旋转90°到达线段NO的位置，在这个旋转过程中，旋转中心是O，旋转角是____，它等于____度.‎ ‎10.平面直角坐标系中有一个点A(-2，6)，则与点A关于原点对称的点的坐标是____，则经过这两点的直线的解析式为____.‎ ‎11.一条线段绕其上一点旋转90°后与原来的线段____.‎ ‎12.如图所示，直线EF过平行四边形ABCD对角线的交点O，且分别交AD、BC于E、F，那么阴影部分的面积是平行四边形ABCD面积的____.‎ 三、解答题(共60分)‎ ‎13.(10分)如图，在△ABC中，∠B=10°，∠ACB=20°，AB=4 cm，△ABC逆时针旋转一定角度后与△ADE重合，且点C恰好成为AD中点.‎ ‎(1)指出旋转中心，并求出旋转角的度数；‎ ‎(2)求出∠BAE的度数和AE的长.‎ ‎14.(12分)如图所示，△DEF是由△ABC绕点O顺时针旋转180°后形成的图形；‎ ‎(1)请你指出图中所有相等的线段；‎ ‎(2)图中哪些三角形可以被看成是关于点O成中心对称关系？‎ ‎15.(12分)如图所示，在△ABC中，AD是BC边上的中线.‎ ‎(1)画出与△ACD关于点D成中心对称的三角形；‎ ‎(2)找出与AC相等的线段；‎ ‎(3)探究：△ABC中AB与AC的和与中线AD之间有何大小关系？并说明理由；‎ ‎(4)若AB=5，AC=3，求线段AD的取值范围.‎ ‎16.(12分)在如图所示的方格图中，我们称每个小正方形的顶点为“格点”，以格点为顶点的三角形叫做“格点三角形”，根据图形，解决下面的问题：‎ ‎(1)图中的格点△A′B′C′是由格点△ABC通过哪些方法变换得到的？‎ ‎(2)设每个小正方形的边长为1，如果建立平面直角坐标系后，点A的坐标为(-3，4)，请写格点△DEF各顶点的坐标，并求出△DEF的面积.‎ ‎17.(14分)已知：如图，在△ABC中，AB=AC，若将△ABC顺时针旋转180°得到△FEC.‎ ‎(1)试猜想AE与BF有何关系，说明理由；‎ ‎(2)若△ABC的面积为3 cm2，求四边形ABFE的面积；‎ ‎(3)当∠ACB为多少度时，四边形ABFE为矩形，说明理由.‎ 参考答案 ‎1.D 2.A 3.A 4.B 5.A 6.C 7.A 8.B ‎9.90 10.(2，-6)，y=-3x. 11.垂直. 12..‎ ‎13.(1)旋转中心为点A，旋转角∠BAD的度数为150°；‎ ‎(2)∠BAE=60°，AE=2 cm.‎ ‎14(1)图中相等的线段有：AB=DE，AC=DF，BC=EF，AO=DO，BO=EO，CO=FO；‎ ‎(2)图中关于点O成中心对称的三角形有：△ABC与△DEF，△ABO与△DEO，△ACO与△DFO，△BCO与△EFO.‎ ‎15.(12分)如图所示，在△ABC中，AD是BC边上的中线.‎ ‎(1)如图所示，△A′BD即为所求；‎ ‎(2)A′B=AC；‎ ‎(3)AB+AC＞2AD，理由：由于△A′BD与△ACD关于点D成中心对称，所以AD=A′D，AC=A′B，在△ABA′中，有AB+A′B＞AA′，即AB+AC＞AD+A′D，因此AB+AC＞2AD；‎ ‎(4)由(3)可得，在△ABA′中，有AB-A′B＜AA′＜AB+A′B，即AB-AC＜2AD＜AB+AC，因此有2＜2AD＜8，所以1＜AD＜4.‎ ‎16.(1)方法不唯一，如：先把△ABC向右平移5小格，使点C移到点C′，再以点C′为旋转中心，顺时针方向旋转90°得到△A′B′C′.‎ ‎(2)D(0，-2)，E(-4，-4)，F(2，-3)，显然点G在DE上，且是DE的中点，则S△DEF=S△DGF+S△GFE==4.‎ ‎17.(1)由旋转可知：AC=CF，BC=CE，∠ACE=∠BCF，‎ ‎∴△ACE≌△BCF（SAS），‎ ‎∴AE=BF，∠CAE=∠CFB，∴AE∥BF，‎ 即AE与BF的关系为：AE∥BF且AE=BF.‎ ‎(2)∵△ACE≌△BCF，∴S△ACE=S△BCF，又∵BC=CE，∴S△ABC=S△ACE，同理：S△CEF=S△BCF，∴S△CEF=S△BCF=S△ACE=S△ABC=3，∴S四边形ABFE=3×4=12(cm2)；‎ ‎(3)当∠ACB=60°时，四边形ABFE为矩形.‎ 理由是：∵BC=CE，AC=CF，∴四边形ABFE为平行四边形，当∠ACB=60°时，∵AB=AC，∴△ABC为等边三角形，∴BC=AC，∴AF=BE，∴四边形ABFE为矩形，即：当∠ACB=60°时，四边形ABFE为矩形.‎