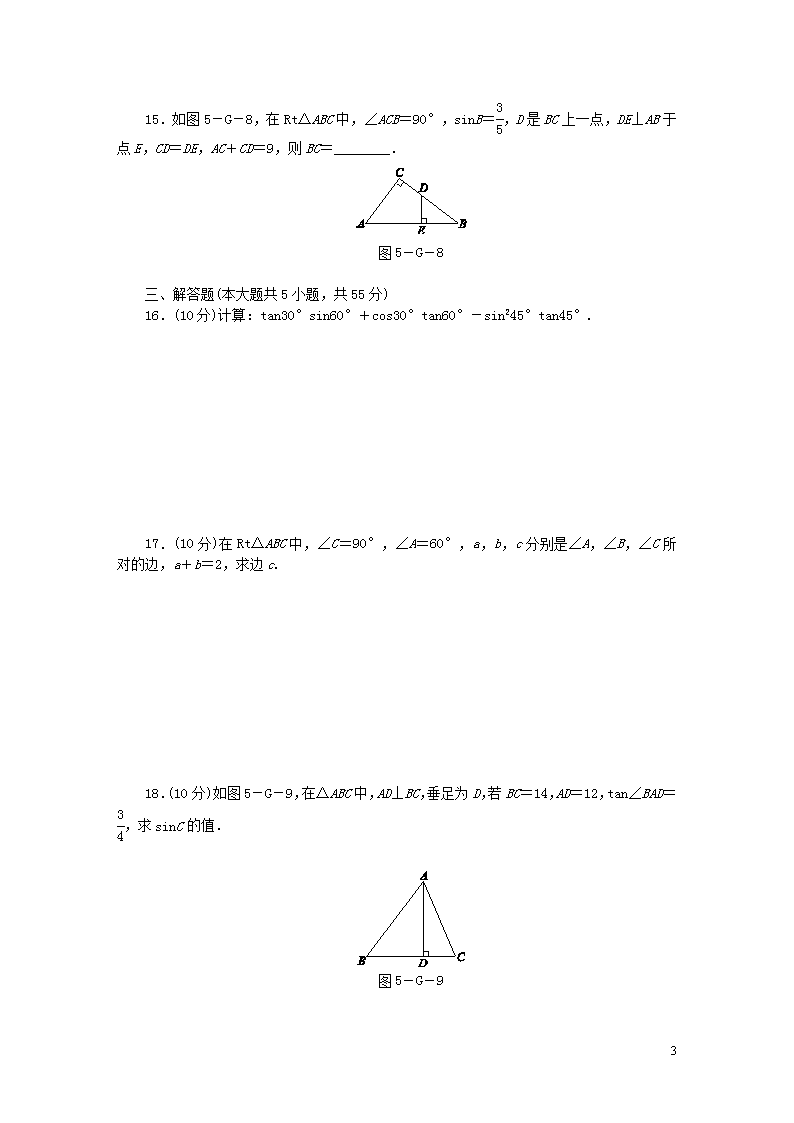2020年秋九年级数学上册 第4章 锐角三角函数 7页

‎4.1～4.3‎ 一、选择题(本大题共8小题，每小题3分，共24分)‎ 图5－G－1‎ ‎1．如图5－G－1，在Rt△ABC中，∠C＝90°，AB＝5，AC＝2，则cosA的值是(　　)‎ A. 　　　B. C. 　　　D. ‎2．如图5－G－2，在Rt△ABC中，∠BAC＝90°，AD⊥BC于点D，则下列结论中不正确的是(　　)‎ A．sinB＝ B．sinB＝ C．sinB＝ D．sinB＝ 图5－G－2‎ ‎　　　‎ 图5－G－3‎ ‎3．如图5－G－3，△ABC的顶点是正方形网格的格点，则sinA的值为(　　)‎ A. B. C. D. ‎4．在Rt△ABC中，cosA＝，则sinA的值是(　　)‎ A. B. C. D. ‎5．计算cos245°＋sin245°的结果是(　　)‎ A. B．‎1 C. D. ‎6．当锐角A＞45°时，sinA的值(　　)‎ A．小于 B．大于 7‎ C．小于 D．大于 ‎7．在△ABC中，∠A，∠B为不相等的锐角，且sinA＝cosB，则这个三角形是(　　)‎ A．等腰三角形 B．锐角三角形 C．钝角三角形 D．直角三角形 ‎8．在△ABC中，AB＝12 ，AC＝13，cosB＝，则BC边的长为(　　)‎ A．7 B．8‎ C．8或17 D．7或17‎ 二、填空题(本大题共7小题，每小题3分，共21分)‎ ‎9．计算：sin60°－tan30°＝________．‎ ‎10．如图5－G－4，在△ABC中，∠C＝90°，AB＝5，BC＝3，则cosA的值是________．‎ 图5－G－4‎ ‎　　　‎ 图5－G－5‎ ‎11．如图5－G－5，将∠AOB放在边长为1的小正方形组成的网格中，则tan∠AOB＝________．‎ ‎12．在△ABC中，∠A，∠B均为锐角，若＋|－sinB|＝0，则∠C＝________°.‎ ‎13．如图5－G－6，在菱形ABCD中，DE⊥AB于点E，DE＝‎6 cm，sinA＝，则菱形ABCD的面积是________ cm2.‎ 图5－G－6‎ ‎　　　‎ 图5－G－7‎ ‎14．如图5－G－7所示，△ABC的三个顶点分别在边长为1的正方形网格的格点上，则tan(α＋β)________tanα＋tanβ.(填“＞”“＝”或“＜”)‎ 7‎ ‎15．如图5－G－8，在Rt△ABC中，∠ACB＝90°，sinB＝，D是BC上一点，DE⊥AB于点E，CD＝DE，AC＋CD＝9，则BC＝________．‎ 图5－G－8‎ 三、解答题(本大题共5小题，共55分)‎ ‎16．(10分)计算：tan30°sin60°＋cos30°tan60°－sin245°tan45°.‎ ‎17．(10分)在Rt△ABC中，∠C＝90°，∠A＝60°，a，b，c分别是∠A，∠B，∠C所对的边，a＋b＝2，求边c.‎ ‎18．(10分)如图5－G－9，在△ABC中，AD⊥BC，垂足为D，若BC＝14，AD＝12，tan∠BAD＝，求sinC的值．‎ 图5－G－9‎ 7‎ ‎19．(12分)已知两角和的正切公式是tan(α＋β)＝，试求tan75°的值．‎ ‎20．(13分)如图5－G－10，△ABC中，∠ACB＝90°，sinA＝，BC＝8，D是AB的中点，过点B作直线CD的垂线，垂足为E.‎ ‎(1)求线段CD的长；‎ ‎(2)求cos∠ABE的值．‎ 图5－G－10‎ ‎　　　　‎ 7‎ ‎1．B　[解析] ∵Rt△ABC中，∠C＝90°，AB＝5，AC＝2，∴cosA＝＝.故选B.‎ ‎2．C　[解析] 在Rt△ABC中，∠BAC＝90°，‎ ‎∴∠B＋∠C＝90°，sinB＝.∵AD⊥BC，‎ ‎∴∠DAC＋∠C＝90°，sinB＝，∴∠B＝∠DAC，∴sinB＝sin∠DAC＝.综上，只有C不正确．故选C.‎ ‎3．B ‎4．B　[解析] ∵cosA＝，∴∠A＝60°，‎ ‎∴sinA＝.‎ ‎5．B　[解析] ∵cos45°＝sin45°＝，∴cos245°＋sin245°＝()2＋()2＝＋＝1.‎ ‎6．B　7.D ‎8．D　[解析] ∵cosB＝，∴∠B＝45°.‎ 当△ABC为钝角三角形时，过点A作AD⊥BC，交BC的延长线于点D，如图①.‎ ‎∵AB＝12 ，∠B＝45°，∴AD＝BD＝12.‎ ‎∵AC＝13，∴由勾股定理得CD＝5，‎ ‎∴BC＝BD－CD＝12－5＝7；‎ 当△ABC为锐角三角形时，过点A作AD⊥BC于点D，如图②，同理可得BC＝BD＋CD＝12＋5＝17.故选D.‎ ‎9. ‎10.　[解析] ∵在△ABC中，∠C＝90°，AB＝5，BC＝3，∴AC＝＝4，‎ ‎∴cosA＝＝.‎ ‎11.　[解析] 过点A作AD⊥OB，垂足为D，‎ 在Rt△AOD中，AD＝1，OD＝2，‎ 则tan∠AOB＝＝.‎ 7‎ ‎12．75‎ ‎13．60　[解析] AD＝＝‎10 cm，‎ 所以菱形ABCD的边长是10 cm，‎ 则菱形ABCD的面积是10×6＝60(cm2)．‎ ‎14．＞　[解析] 由正方形网格图可知，tanα＝，tanβ＝，则tanα＋tanβ＝＋＝.‎ ‎∵AC＝BC，∠ACB＝90°，‎ ‎∴α＋β＝45°，‎ ‎∴tan(α＋β)＝1，‎ ‎∴tan(α＋β)＞tanα＋tanβ.‎ ‎15．8　[解析] 设DE＝x，则CD＝x，AC＝9－x.‎ ‎∵sinB＝，DE⊥AB，∴BD＝x，‎ 由勾股定理，得BE＝，则tanB＝，‎ ‎∴＝，即＝，解得x＝3，‎ ‎∴BC＝x＋x＝8.‎ 故答案为8.‎ ‎16．解：原式＝×＋×－()2×1＝＋－＝.‎ ‎17．解：∵在Rt△ABC中，∠C＝90°，∠A＝60°，‎ ‎∴∠B＝30°，tanA＝，‎ ‎∴a＝btanA＝b，c＝2b.‎ 又∵a＋b＝2，∴b＋b＝2，‎ ‎∴b＝－1，∴c＝2b＝2 －2.‎ ‎18．解：∵在Rt△ABD中，tan∠BAD＝＝，‎ ‎∴BD＝AD·＝12×＝9，‎ ‎∴CD＝BC－BD＝14－9＝5，‎ ‎∴AC＝＝＝13，‎ ‎∴sinC＝＝.‎ ‎19．解：tan75°＝tan(30°＋45°)＝＝2＋.‎ 7‎ ‎20．解：(1)在△ABC中，∵∠ACB＝90°，‎ ‎∴sinA＝＝，而BC＝8，∴AB＝10.‎ ‎∵D是AB的中点，∴CD＝AB＝5.‎ ‎(2)在Rt△ABC中，∵AB＝10，BC＝8，‎ ‎∴AC＝＝6.‎ ‎∵D是AB的中点，∴BD＝5，S△BDC＝S△ADC，‎ ‎∴S△BDC＝S△ABC，‎ 即CD·BE＝·AC·BC，‎ ‎∴BE＝＝.‎ 在Rt△BDE中，cos∠DBE＝＝＝，‎ 即cos∠ABE的值为.‎ 7‎