- 642.50 KB
- 2021-11-06 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
1.2
矩形的性质与判定
第一章 特殊平行四边形
第
2
课时 矩形的判定
导入新课
讲授新课
当堂练习
课堂小结
1
.理解并掌握矩形的判定方法.(重点)
2
.能应用矩形判定解决简单的证明题和计算题
.
(
难点
)
学习目标
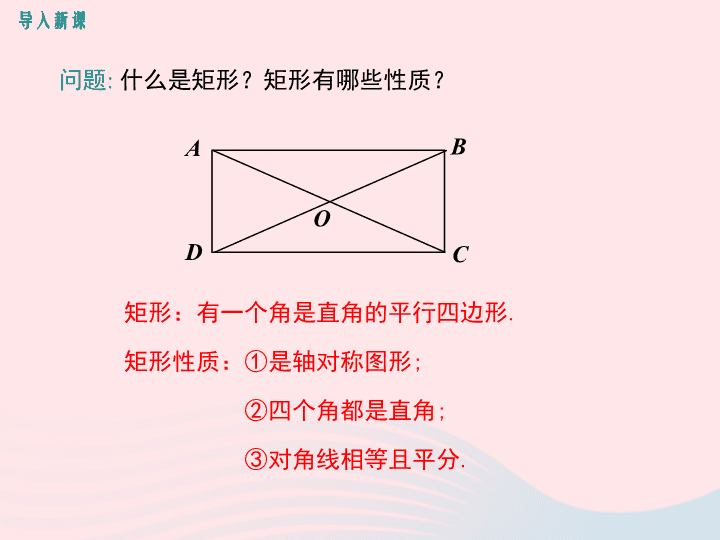
问题
:
什么是矩形?矩形有哪些性质?
A
B
C
D
O
矩形:有一个角是直角的平行四边形
.
矩形性质:
①
是轴对称图形
;
②四个角都是直角
;
③
对角线相等且平分
.
导入新课
矩形判定的定理及其证明
一
活动
1:
利用一个活动的平行四边形教具演示
,
拉动一对不相邻的顶点时
,
注意观察
两条对角线的长度
.
问题
1:
我们会看到对角线会随着∠
α
变化而变化
,
当两条对角线长度相等时
,
平行四边形有什么特征?
α
讲授新课
已知:如图
,
在
□
ABCD
中
,
AC
,
DB
是它的两条对角线
,
AC
=
DB
.
求证:
□
ABCD
是矩形
.
证明:∵
AB
=
DC
,
BC
=
CB
,
AC
=
DB
,
∴ △
ABC
≌
△
DCB
,
∴∠
ABC
=
∠
DCB
.
∵
AB
∥
CD
,
∴∠
ABC
+
∠
DCB
= 180°
,
∴ ∠
ABC
= 90°
,
∴
□
ABCD
是矩形(矩形的定义)
.
猜想
:
当对角线相等时,该平行四边形可能是矩形
.
A
B
C
D
对角线相等的平行四边形是矩形
.
定理
活动
2:
李芳同学通过画
“
边-直角、边-直角、边-直角、边
”
这样四步画出一个四边形
.
①
②
③
④
问题
2:
李芳觉得按照以上步骤可以得到一个矩形?你认为她的判断正确吗?如果正确
,
你能证明吗?
已知:如图
,
在四边形
ABCD
中
,∠
A
=∠
B
=∠
C
=
90
°
.
求证:四边形
ABCD
是矩形
.
猜想
:
当三个角都是直角
,
该四边形可能是矩形
.
证明
:∵ ∠
A
=∠
B
=∠
C
=90
°
,
∴∠
A
+
∠
B
=180
°
,
∠
B
+∠
C
=180
°
.
∴
AD
∥
BC
,
AB
∥
CD
.
∴
四边形
ABCD
是平行四边形
.
∴
四边形
ABCD
是矩形
.
A
B
C
D
有三个角是直角的四边形是矩形
.
定理
例
1
:
如图
,
在
□
ABCD
中
,
对角线
AC
与
BD
相交于点
O
,
△
ABO
是等边三角形
,
AB
=4
,
求
□
ABCD
的面积
.
解:∵四边形
ABCD
是平行四边形
,
∴
OA
=
OC
,
OB
=
OD
.
又∵
△
ABO
是等边三角形
,
∴
OA
=
OB
=
AB
= 4
,
∠
BAC
=60°.
∴
AC
=
BD
= 2
OA
= 2×4 = 8.
定理的应用
二
典例精析
A
B
C
D
O
∴
□ABCD
是矩形
(
对角线相等的平行四边形是矩形
)
.
∴∠
ABC
=90°
(矩形的四个角都是直角)
.
在
Rt
△
ABC
中
,
由勾股定理
,
得
AB
2
+
BC
2
=
AC
2
,
∴
BC
= .
∴
S
□ABCD
=
AB
·
BC
=
4× =
A
B
C
D
O
例
2
:
如图,在
△
ABC
中
,
AB
=
AC
,
D
为
BC
上一点,以
AB
,
BD
为邻边作平行四边形
ABDE
,
连接
AD
,
EC
.
(
1
)求证:△
ADC
≌
△
ECD
;
(
2
)若
BD
=
CD
,
求证:四边形
ADCE
是矩形
.
证明:(
1
)∵
△
ABC
是等腰三角形
,
∴
∠
B
=
∠
ACB
.
又∵四边形
ABDE
是平行四边形
,
∴
∠
B
=
∠
EDC
,
AB
=
DE
,
∴
∠
ACB=
∠
EDC
,
∴
△
ADC
≌
△
ECD
.
A
D
C
E
B
(2)
∵
AB
=
AC
,
BD
=
CD
,
∴
AD
⊥
BC
,
∴
∠
ADC
=90°.
∵四边形
ABDE
是平行四边形
,
∴
AE
平行且等于
BD
,
即
AE
平行且等于
DC
,
∴
四边形
ADCE
是平行四边形
.
而∠
ADC
=90°
,
∴四边形
ADCE
是矩形
.
A
D
C
E
B
1.
如图
,
直线
EF
∥
MN
,
PQ
交
EF
、
MN
于
A
、
C
两点
,
AB
、
CB
、
CD
、
AD
分别是
∠
EAC
、
∠
MCA
、
∠
ACN
、
∠
CAF
的角平分线
,
则四边形
ABCD
是( )
A.
菱形
B.
平行四边形
C.
矩形
D.
不能确定
D
E
F
M
N
Q
P
A
B
C
C
当堂练习
2.
如图,
O
是菱形
ABCD
对角线的交点,作
DE
∥
AC
,
CE
∥
BD
,
DE
、
CE
交于点
E
,四边形
CEDO
是矩形吗?说出你的理由
.
D
A
B
C
E
O
解:四边形
CEDO
是矩形
.
理由如下:已知四边形
ABCD
是菱形
.
∴
AC
⊥
BD
.
∴∠
BOC
=90°.
∵
DE∥AC
,
CE
∥
BD
,
∴
四边形
CEDO
是平行四边形
.
∴四边形
CEDO
是矩形(矩形的定义)
.
有一个角是直角的平行四边形是矩形
.
定理
1
:对角线相等的平行四边形是矩形
.
定理
2
:有三个角是直角的四边形是矩形
.
运用定理进行计算和证明
.
矩形的判定
定义
定理
课堂小结
相关文档
- 北师大版数学九年级上册同步练习课2021-11-0610页
- 北师大版数学九年级上册同步练习课2021-11-0614页
- 2019九年级数学上册 第一章 特殊平2021-11-066页
- 北师大版数学九年级上册同步练习课2021-11-0620页
- 九年级数学上册第一章特殊平行四边2021-11-0610页
- 2020九年级数学上册 第一章 特殊平2021-11-069页
- 九年级数学上册第一章特殊平行四边2021-11-064页
- 九年级数学上册第一章特殊平行四边2021-11-0626页
- 九年级数学上册第一章特殊平行四边2021-11-062页
- 浙教版数学八年级下册第5章《特殊2021-11-017页