2019九年级数学下册 第1章专题训练 解直角三角形应用中的基本模型 10页

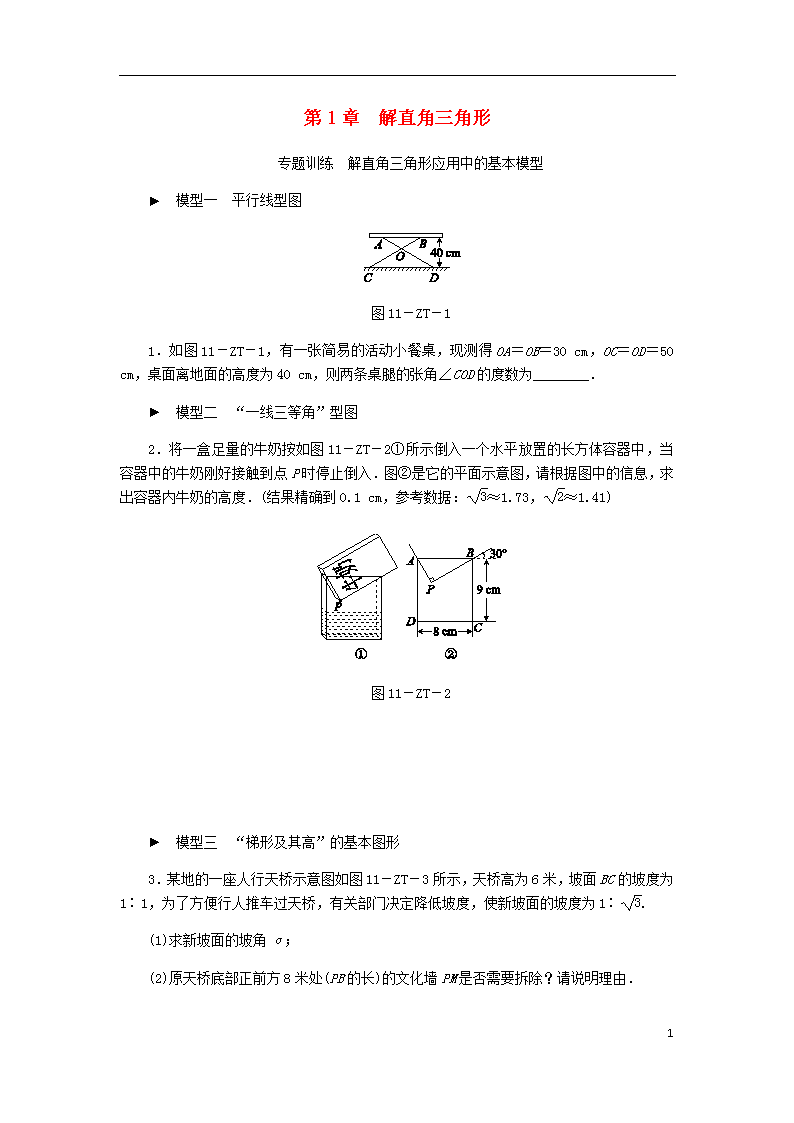
第1章　解直角三角形 专题训练　解直角三角形应用中的基本模型 ‎►　模型一　平行线型图 图11－ZT－1‎ ‎1．如图11－ZT－1，有一张简易的活动小餐桌，现测得OA＝OB＝‎30 cm，OC＝OD＝‎50 cm，桌面离地面的高度为‎40 cm，则两条桌腿的张角∠COD的度数为________．‎ ‎►　模型二　“一线三等角”型图 ‎2．将一盒足量的牛奶按如图11－ZT－2①所示倒入一个水平放置的长方体容器中，当容器中的牛奶刚好接触到点P时停止倒入．图②是它的平面示意图，请根据图中的信息，求出容器内牛奶的高度．(结果精确到‎0.1 cm，参考数据：≈1.73，≈1.41)‎ 图11－ZT－2‎ ‎►　模型三　“梯形及其高”的基本图形 ‎3．某地的一座人行天桥示意图如图11－ZT－3所示，天桥高为‎6米，坡面BC的坡度为1∶1，为了方便行人推车过天桥，有关部门决定降低坡度，使新坡面的坡度为1∶.‎ ‎(1)求新坡面的坡角α；‎ ‎(2)原天桥底部正前方‎8米处(PB的长)的文化墙PM是否需要拆除？请说明理由．‎ 10‎ 图11－ZT－3‎ ‎►　模型四　“锐角三角形及其高”的基本图形 ‎4．2017·成都科技改变生活，手机导航极大地方便了人们的出行．如图11－ZT－4，小明一家自驾到古镇C游玩，到达A地后，导航显示车辆应沿北偏西60°方向行驶‎4千米至B地，再沿北偏东45°方向行驶一段距离到达古镇C，小明发现古镇C恰好在A地的正北方向，求B，C两地之间的距离．‎ 图11－ZT－4‎ 10‎ ‎5．如图11－ZT－5，湖中的小岛上有一标志性建筑物，其底部为A，某人在岸边的B处测得A在B的北偏东30°的方向上，然后沿岸边直行‎4千米到达C处，再次测得A在C的北偏西45°的方向上(其中A，B，C在同一个平面上)．求这个标志性建筑物的底部A到岸边BC的最短距离．‎ 图11－ZT－5‎ ‎►　模型五　“钝角三角形及钝角一边上的高”的基本图形 ‎6．某国发生8.1级强烈地震，我国积极组织抢险队赴地震灾区参与抢险工作，如图11－ZT－6，某探测器在地面A，B两处均探测出建筑物下方C处有生命迹象，已知探测线与地面的夹角分别是25°和60°，且AB＝‎4米，求该生命迹象所在位置C的深度．(结果精确到‎1米，参考数据：sin25°≈0.4，cos25°≈0.9，tan25°≈0.5，≈1.7)‎ 图11－ZT－6‎ ‎7．2017·内江如图11－ZT－7，某人为了测量山顶上的塔ED的高度，他在山下的点A 10‎ 处测得塔尖点D的仰角为45°，再沿AC方向前进‎60 m到达山脚点B，测得塔尖点D的仰角为60°，塔底点E的仰角为30°，求塔ED的高度．(结果保留根号)‎ 图11－ZT－7‎ ‎8．2017·白银美丽的黄河宛如一条玉带穿城而过，沿河两岸的滨河路风情线是兰州最美的景观之一．数学课外实践活动中，小林在南滨河路上的A，B两点处，利用测角仪分别对北岸的一观景亭D进行了测量．如图11－ZT－8，测得∠DAC＝45°，∠DBC＝65°.若AB＝‎132米，求观景亭D到南滨河路AC的距离约为多少米．(结果精确到‎1米，参考数据：sin65°≈0.91，cos65°≈0.42，tan65°≈2.14)‎ 图11－ZT－8‎ 10‎ ‎9．如图11－ZT－9，禁止捕鱼期间，某海上稽查队在某海域巡逻，上午某一时刻在A处接到指挥部通知，在他们东北方向距离12海里的B处有一艘捕鱼船，正在沿南偏东75°方向以每小时10海里的速度航行，稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发，在C处成功拦截捕鱼船，求巡逻船从出发到成功拦截捕鱼船所用的时间．‎ 图11－ZT－9‎ 10‎ 详解详析 ‎1．120°　[解析] 作AF⊥CD于点F，则AF＝‎40 cm，AD＝OA＋OD＝‎80 cm.于是可得sin∠ADC＝＝，∴∠ADC＝30°.‎ ‎∵OC＝OD，∴∠COD＝120°.‎ ‎2．解：过点P作EF⊥AD交AD于点E，交BC于点F.‎ 设BF＝x.∵∠BAD＝∠AEF＝∠ABC＝90°，‎ ‎∴四边形AEFB是矩形，∴AE＝BF＝x.‎ 在Rt△BPF中，∠BFP＝90°，∠BPF＝30°，‎ tan∠BPF＝，∴PF＝＝x.‎ 在Rt△AEP中，∵∠AEP＝90°，∠APE＝90°－∠BPF＝60°，PE＝8－x，tan∠APE＝，‎ ‎∴＝，化简得x＝8 －3x，‎ 解得x＝2 ≈3.46(cm)，‎ ‎∴BF≈3.46(cm)，‎ ‎∴容器内牛奶的高度＝CF＝9－BF≈5.5(cm)．即容器内牛奶的高度约为5.5 cm.‎ ‎3．解：(1)∵新坡面的坡度为1∶，‎ ‎∴tanα＝tan∠CAB＝＝，‎ ‎∴α＝30°.‎ 10‎ 答：新坡面的坡角α为30°.‎ ‎(2)文化墙PM不需要拆除．‎ 理由：过点C作CD⊥AB于点D，‎ 则CD＝6米．‎ ‎∵坡面BC的坡度为1∶1，新坡面的坡度为1∶，‎ ‎∴BD＝CD＝6米，AD＝6 米，‎ ‎∴AB＝AD－BD＝(6 －6)米＜8米，‎ ‎∴文化墙PM不需要拆除．‎ ‎4．解：如图，由题意知：AB＝‎4千米，∠CAB＝60°，∠CBD＝45°，AC∥BD，‎ 过点B作BE⊥AC于点E，‎ ‎∴∠CEB＝90°，∠EBA＝90°－∠CAB＝30°，∠CBE＝90°－∠CBD＝45°，‎ ‎∴BE＝AB·cos30°＝4×＝2 (千米)，‎ ‎∴BC＝BE＝×2 ＝2 (千米)，‎ 即B，C两地之间的距离为2 千米．‎ ‎5．解：过点A作AD⊥BC于点D，则AD的长度即为A到岸边BC的最短距离．‎ 在Rt△ACD中，∠ACD＝45°，‎ 设AD＝x千米，则CD＝AD＝x千米．‎ 在Rt△ABD中，∠ABD＝60°，‎ 10‎ 由tan∠ABD＝，即tan60°＝，‎ ‎∴BD＝＝x(千米)．‎ 又BC＝4千米，即BD＋CD＝4千米，‎ ‎∴x＋x＝4，解得x＝6－2 .‎ 即小岛上标志性建筑物的底部A到岸边BC的最短距离为(6－2 )千米．‎ ‎6．解：过点C作CD⊥AB交AB的延长线于点D，设CD＝x米．‎ 在Rt△ADC中，∠DAC＝25°，‎ 所以tan25°＝≈0.5，所以AD≈＝2x米．‎ 在Rt△BDC中，∠DBC＝60°，由tan60°＝＝，解得x≈3.‎ 即该生命迹象所在位置C的深度约为3米．‎ ‎7．解：由题意知∠DBC＝60°，∠EBC＝30°，‎ ‎∴∠DBE＝∠DBC－∠EBC＝60°－30°＝30°.‎ 又∵∠BCD＝90°，‎ ‎∴∠BDC＝90°－∠DBC＝90°－60°＝30°，‎ ‎∴∠DBE＝∠BDE，‎ ‎∴BE＝ED.‎ 设EC＝x m，则ED＝BE＝2EC＝2x m，DC＝EC＋ED＝x＋2x＝3x(m)，‎ BC＝＝x m.‎ 由题意可知∠DAC＝45°，∠DCA＝90°，‎ ‎∴△ACD为等腰直角三角形，∴AC＝DC，‎ 10‎ ‎∴x＋60＝3x 解得x＝30＋10 .‎ 则ED＝2x＝(60＋20 )m.‎ 答：塔ED的高度约为(60＋20 )m.‎ ‎8．解：如图，过点D作DE⊥AC，垂足为E，设BE＝x米．‎ 在Rt△DEB中，tan∠DBE＝，‎ ‎∵∠DBC＝65°，‎ ‎∴DE＝xtan65°米．‎ 在Rt△ADE中，‎ ‎∵∠DAC＝45°，‎ ‎∴AE＝DE，‎ ‎∴132＋x＝xtan65°，‎ 解得x≈115.8，‎ ‎∴DE≈248米．‎ 即观景亭D到南滨河路AC的距离约为248米．‎ ‎9．解：设巡逻船从出发到成功拦截捕鱼船所用的时间为x小时．‎ 由题意得∠ABC＝45°＋75°＝120°，AB＝12海里，BC＝10x海里，AC＝14x海里．‎ 如图，过点A作AD⊥CB交其延长线于点D.‎ 在Rt△ABD中，AB＝12海里，∠ABD＝60°，‎ 10‎ ‎∴BD＝AB·cos60°＝AB＝6海里，AD＝AB·sin60°＝6 海里，∴CD＝(10x＋6)海里．‎ 在Rt△ACD中，由勾股定理得(14x)2＝(10x＋6)2＋(6 )2，‎ 解得x1＝2，x2＝－(不合题意，舍去)．‎ 答：巡逻船从出发到成功拦截捕鱼船所用的时间为2小时．‎ 10‎