- 202.00 KB
- 2021-11-06 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
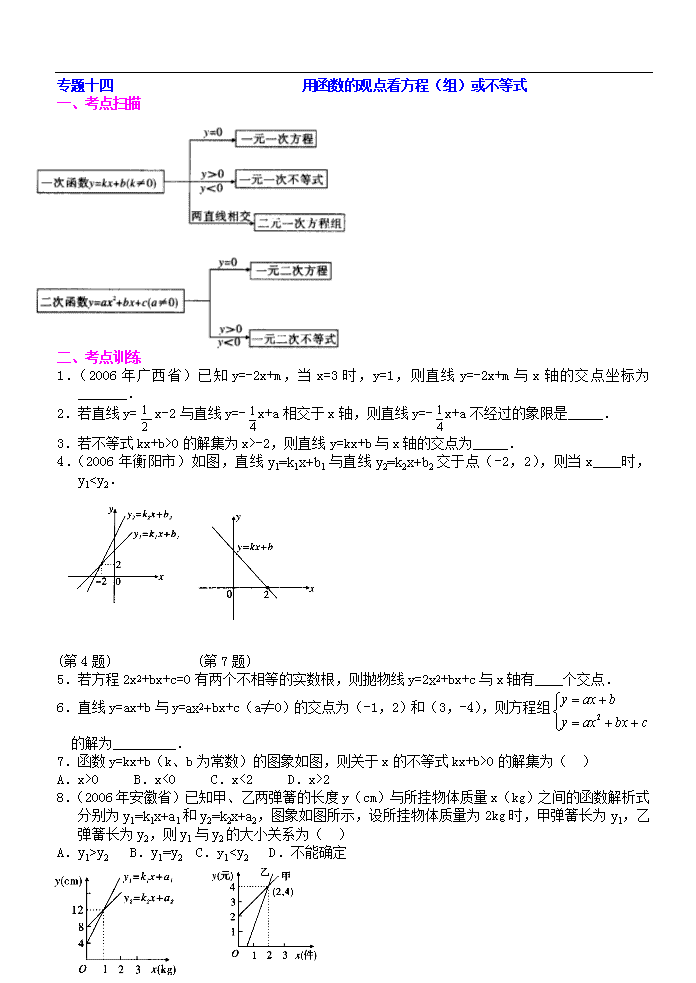
专题十四 用函数的观点看方程(组)或不等式
一、考点扫描
二、考点训练
1.(2006年广西省)已知y=-2x+m,当x=3时,y=1,则直线y=-2x+m与x轴的交点坐标为_______.
2.若直线y=x-2与直线y=-x+a相交于x轴,则直线y=-x+a不经过的象限是_____.
3.若不等式kx+b>0的解集为x>-2,则直线y=kx+b与x轴的交点为_____.
4.(2006年衡阳市)如图,直线y1=k1x+b1与直线y2=k2x+b2交于点(-2,2),则当x____时,y10的解集为( )
A.x>0 B.x<0 C.x<2 D.x>2
8.(2006年安徽省)已知甲、乙两弹簧的长度y(cm)与所挂物体质量x(kg)之间的函数解析式分别为y1=k1x+a1和y2=k2x+a2,图象如图所示,设所挂物体质量为2kg时,甲弹簧长为y1,乙弹簧长为y2,则y1与y2的大小关系为( )
A.y1>y2 B.y1=y2 C.y1y2.
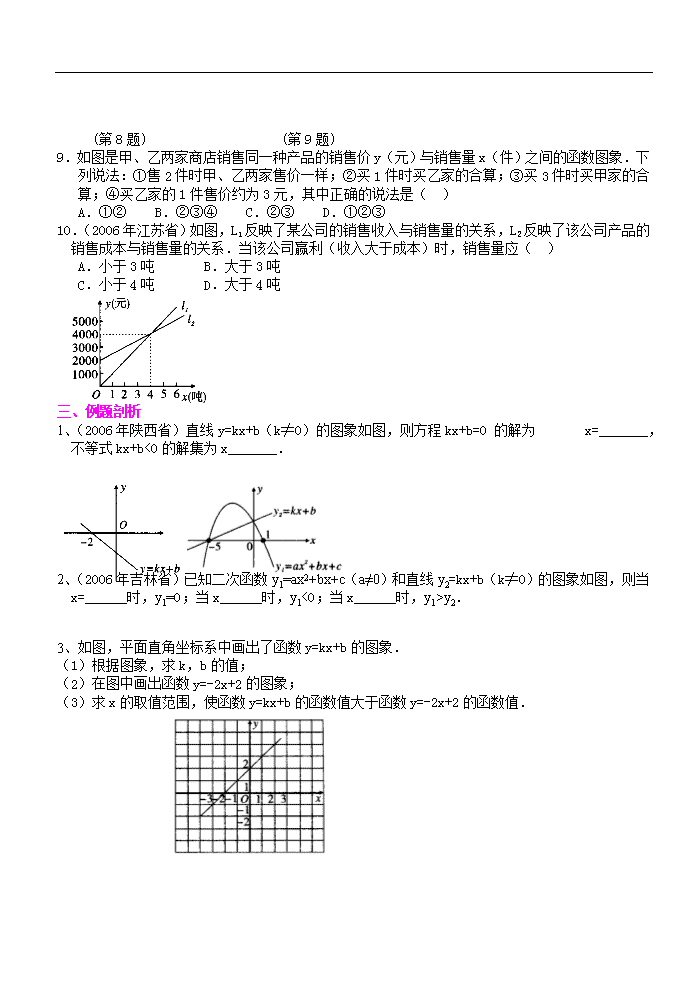
3、如图,平面直角坐标系中画出了函数y=kx+b的图象.
(1)根据图象,求k,b的值;
(2)在图中画出函数y=-2x+2的图象;
(3)求x的取值范围,使函数y=kx+b的函数值大于函数y=-2x+2的函数值.
4、育才中学需要添置某种教学仪器.方案1:到商
购买,每件需要8元;方案2:学校自己制作,每
件4元,另外需要制作工具的租用费120元.设需要
仪器x件,方案1与方案2的费用分别为y1,y2(元).
(1)分别写出y1,y2的函数表达式;
(2)当购置仪器多少件时,两种方案的费用相同?
(3)若学校需要仪器50件,问采用哪种方案便宜?请说明理由.
5、如图表示一艘轮船和一艘快艇沿相同路线从甲港出
发到乙港行驶过程中路程随时间变化的图象(分别是
正比例函数图象和一次函数图象),根据图象解答下
列问题:
(1)请分别求出表示轮船和快艇行驶过程的函数解析式(不要求写出自变量的取值范围);
(2)轮船和快艇在途中(不包括起点和终点)行驶的速度分别是多少?
(3)问快艇出发多长时间赶上轮船?
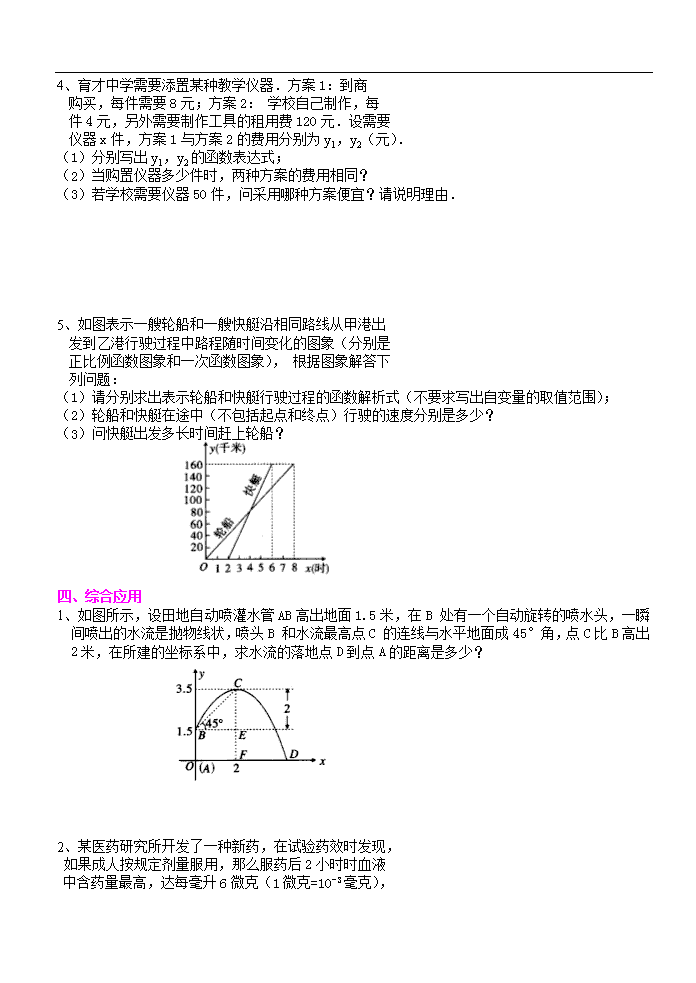
四、综合应用
1、如图所示,设田地自动喷灌水管AB高出地面1.5米,在B处有一个自动旋转的喷水头,一瞬间喷出的水流是抛物线状,喷头B和水流最高点C的连线与水平地面成45°角,点C比B高出2米,在所建的坐标系中,求水流的落地点D到点A的距离是多少?
2、某医药研究所开发了一种新药,在试验药效时发现,
如果成人按规定剂量服用,那么服药后2小时时血液
中含药量最高,达每毫升6微克(1微克=10-3毫克),
接着逐步衰减,10小时时血液中含药量为每毫升3
微克,每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示.当成人按规定剂量服药后:
(1)分别求出x≤2和x≥2时x与y之间的函数关系式;
(2)如果每毫升血液中含药量为4微克或4微克以上时在治疗疾病时是有效的,那么这个有效时间是多长?
(一)方程、函数型
此类题目往往要求所设计的问题中出现路程最短、运费最少、效率最高等词语,解题时常常与函数、几何联系在一起.
1..(2007山东青岛)某饮料厂开发了A、B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A、B两种饮料共100瓶.设生产A种饮料x瓶,解答下列问题:
(1)有几种符合题意的生产方案?写出解答过程;
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低?
原料名称
饮料名称
甲
乙
A
20克
40克
B
30克
20克
2.(2007重庆)我市某镇组织20辆汽车装运完A、B、C三种脐橙共100吨到外地销售.按计划,20辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满.根据下表提供的信息,解答以下问题:
脐 橙 品 种
A
B
C
每辆汽车运载量(吨)
6
5
4
每吨脐橙获得(百元)
12
16
10
(1)设装运A种脐橙的车辆数为,装运B种脐橙的车辆数为,求与之间的函数关系式;
(2)如果装运每种脐橙的车辆数都不少于4辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
3.(05资阳)甲、乙两同学开展“投球进筐”比赛,双方约定:①
比赛分6局进行,每局在指定区域内将球投向筐中,只要投进一次后该局便结束;② 若一次未进可再投第二次,以此类推,但每局最多只能投8次,若8次投球都未进,该局也结束;③ 计分规则如下:a. 得分为正数或0;b. 若8次都未投进,该局得分为0;c. 投球次数越多,得分越低;d. 6局比赛的总得分高者获胜 .
(1) 设某局比赛第n(n=1,2,3,4,5,6,7,8)次将球投进,请你按上述约定,用公式、表格或语言叙述等方式,为甲、乙两位同学制定一个把n换算为得分M的计分方案;
(2) 若两人6局比赛的投球情况如下(其中的数字表示该局比赛进球时的投球次数,“×”表示该局比赛8次投球都未进):
第一局
第二局
第三局
第四局
第五局
第六局
甲
5
×
4
8
1
3
乙
8
2
4
2
6
×
根据上述计分规则和你制定的计分方案,确定两人谁在这次比赛中获胜.
4.(2007广东梅州)梅林中学租用两辆小汽车(设速度相同)同时送1名带队老师及7名九年级的学生到县城参加数学竞赛,每辆限坐4人(不包括司机).其中一辆小汽车在距离考场15km的地方出现故障,此时离截止进考场的时刻还有42分钟,这时唯一可利用的交通工具是另一辆小汽车,且这辆车的平均速度是60km/h,人步行的速度是5km/h(上、下车时间忽略不计).
(1)若小汽车送4人到达考场,然后再回到出故障处接其他人,请你能过计算说明他们能否在截止进考场的时刻前到达考场;
(2)假如你是带队的老师,请你设计一种运送方案,使他们能在截止进考场的时刻前到达考场,并通过计算说明方案的可行性.
5.(2007哈尔滨)青青商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件恰好用去2700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润(利润=售价进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案;
(3)在“五·一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:
打折前一次性购物总金额
优惠措施
不超过300元
不优惠
超过300元且不超过400元
售价打九折
超过400元
售价打八折
按上述优惠条件,若小王第一天只购买甲种商品一次性付款200元,第二天只购买乙种商品打折后一次性付款324元,那么这两天他在该商场购买甲、乙两种商品一共多少件?(通过计算求出所有符合要求的结果)
6.(07茂名市)已知甲、乙两辆汽车同时、同方向从同一地点A出发行驶.
(1)若甲车的速度是乙车的2倍,甲车走了90千米后立即返回与乙车相遇,相遇时乙车走了1小时.求甲、乙两车的速度;
(2)假设甲、乙每辆车最多只能带200升汽油,每升汽油可以行驶10千米,途中不能再加油,但两车可以互相借用对方的油,若两车都必须沿原路返回到出发点A,请你设计一种方案使甲车尽可能地远离出发点A,并求出甲车一共行驶了多少千米?
7、(2007哈尔滨)青青商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件恰好用去2700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润(利润=售价
进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案;
(3)在“五·一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:
打折前一次性购物总金额
优惠措施
不超过300元
不优惠
超过300元且不超过400元
售价打九折
超过400元
售价打八折
按上述优惠条件,若小王第一天只购买甲种商品一次性付款200元,第二天只购买乙种商品打折后一次性付款324元,那么这两天他在该商场购买甲、乙两种商品一共多少件?(通过计算求出所有符合要求的结果)
(二)测量设计型
设计测量方案题渗透到几何各章节之中,例如:测量底部不能直接到达的小山的高,测量池塘的宽度,测量圆的直径等,此类题目解法不惟一,是典型的开放型试题.
8.(07资阳)图7
一座建于若干年前的水库大坝的横断面如图7所示,其中背水面的整个坡面是长为90米、宽为5米的矩形. 现需将其整修并进行美化,方案如下:① 将背水坡AB的坡度由1∶0.75改为1∶;② 用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域,依次相间地种草与栽花 .
⑴ 求整修后背水坡面的面积;
⑵ 如果栽花的成本是每平方米25元,种草的成本是每平方米20元,那么种植花草至少需要多少元?
9.(05宁波)沪杭甬高速公路拓宽宁波段工程进入全面施工阶段,在现有双向四车道的高速公路两侧经加宽形成双向八车道.如图,路基原横断面为等腰梯形ABCD,AD∥BC,斜坡DC的坡度为i1,在其一侧加宽DF=7.75米,点E、F分别在BC、AD的延长线上,斜坡FE的坡度为i2(i1<i2).设路基的高DM=h米,拓宽后横断面一侧增加的四边形DCEF的面积为s米2.
(1)已知i2=1:1.7,h=3米,求ME 的长.
(1) 不同路段的i1、i2、、、h是不同的,请你设计一个求面积S的公式(用含i1、i2的代数式表示).(通常把坡面的铅直高度与水平宽度的比叫做坡度.坡度常用字母i表示,即i=,通常写成1:m的形式)
三:设计最佳方案型
此类题目往往要求所设计的问题中出现路程最短、运费最少、效率最高等词语,解题时常常与函数、几何联系在一起.
10.(2007四川绵阳)绵阳市“全国文明村”江油白玉村果农王灿收获枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)王灿如何安排甲、乙两种货车可一次性地运到销售地?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王灿应选择哪种方案,使运输费最少?最少运费是多少?
11.(2007四川眉山)某县响应“建设环保节约型社会”的号召,决定资助部分付镇修建一批沼气池,使农民用到经济、环保的沼气能源.幸福村共有264户村民,政府补助村里34万元,不足部分由村民集资.修建A型、B型沼气池共20个.两种型号沼气池每个修建费用、可供使用户数、修建用地情况如下表:
沼气池
修建费用(万元/个)
可供使用户数(户/个)
占地面积(m2/个)
A型
3
20
48
B型
2
3
6
政府相关部门批给该村沼气池修建用地708m2.设修建A型沼气池x个,修建两种型号沼气池共需费用y万元.
(1)求y与x之间的函数关系式;
(2)不超过政府批给修建沼气池用地面积,又要使该村每户村民用上沼气的修建方案有几种;
(3)若平均每户村民集资700元,能否满足所需费用最少的修建方案.
12.(2007重庆)我市某镇组织20辆汽车装运完A、B、C三种脐橙共100吨到外地销售.按计划,20辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满.根据下表提供的信息,解答以下问题:
脐 橙 品 种
A
B
C
每辆汽车运载量(吨)
6
5
4
每吨脐橙获得(百元)
12
16
10
(1)设装运A种脐橙的车辆数为,装运B种脐橙的车辆数为,求与之间的函数关系式;
(2)如果装运每种脐橙的车辆数都不少于4辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
相关文档
- 中考数学专题复习练习:二次根式的加2021-11-0613页
- 中考数学专题复习练习:解直角三角形2021-11-0610页
- 中考数学专题复习练习:正多边形的有2021-11-068页
- 中考数学专题复习练习:关于利用合并2021-11-0611页
- 中考数学专题复习练习:三角形的角平2021-11-064页
- 中考数学专题复习练习:比例线段2021-11-0610页
- 中考数学专题复习练习:相似三角形的2021-11-0630页
- 中考数学专题复习练习:二次根式的化2021-11-068页
- 中考数学专题复习练习:圆心角定理答2021-11-064页
- 中考数学专题复习练习:垂直于弦的直2021-11-065页