正方形的性质与判定教案(2) 3页

第一章 特殊平行四边形 ‎1.3 正方形的性质与判定（二）‎ 教学目标:‎ 1、 知道正方形的判定方法，会运用平行四边形、矩形、菱形、正方形的判定条件进行有关的论证和计算.‎ 2、 经历探究正方形判定条件的过程，发展学生初步的综合推理能力，主动探究的学习习惯，逐步掌握说理的基本方法.‎ 3、 理解特殊的平行四边形之间的内在联系，培养学生辩证看问题的观点.‎ 教学重点：掌握正方形的判定条件.‎ 教学难点：合理恰当地利用特殊平行四边形的判定进行有关的论证和计算.‎ 教学过程：‎ 一、创设问题情景，引入新课 我们学习了平行四边形、矩形、菱形、正方形，那么思考一下，它们之间有怎样的包含关系？请填入下图中.‎ ‎ ‎ 通过填写让学生形象地看到正方形是特殊的矩形，也是特殊的菱形，还是特殊的平行四边形；而正方形、矩形、菱形都是平行四边形；矩形、菱形都是特殊的平行四边形.‎ ‎1、怎样判断一个四边形是矩形？‎ ‎2、怎样判断一个四边形是菱形？‎ ‎3、怎样判断一个四边形是平行四边形？‎ ‎4、怎样判断一个平行四边形是矩形、菱形？‎ 议一议：你有什么方法判定一个四边形是正方形？‎ 二、讲授新课 ‎1．探索正方形的判定条件：学生活动：四人一组进行讨论研究，老师巡回其间，进行 引导、质疑、解惑，通过分析与讨论，师生共同总结出判定一个四边形是正方形的基本方法.‎ ‎（1）直接用正方形的定义判定，即先判定一个四边形是平行四边形，若这个平行四边形有一个角是直角，并且有一组邻边相等，那么就可以判定这个平行四边形是正方形；‎ ‎（2）先判定一个四边形是矩形，再判定这个矩形是菱形，那么这个四边形是正方形；‎ ‎（3）先判定四边形是菱形，再判定这个菱形是矩形，那么这个四边形是正方形.‎ 3‎ 后两种判定均要用到矩形和菱形的判定定理.矩形和菱形的判定定理是判定正方形的基础.这三个方法还可写成：有一个角是直角，且有一组邻边相等的四边形是正方形；有一组邻边相等的矩形是正方形；有一个角是直角的菱形是正方形.‎ 上述三种判定条件是判定四边形是正方形的一般方法，可当作判定定理用，但由于判定平行四边形、矩形、菱形的方法各异，所给出的条件各不相同，所以判定一个四边形是不是正方形的具体条件也相应可作变化，在应用时要仔细辨别后才可以作出判断 ‎2．正方形判定条件的应用 ‎【例1】判断下列命题是真命题还是假命题？并说明理由.‎ （1） 四条边相等且四个角也相等的四边形是正方形；‎ （2） 四个角相等且对角线互相垂直的四边形是正方形；‎ （3） 对角线互相垂直平分的四边形是正方形；‎ （4） 对角线互相垂直且相等的四边形是正方形；‎ （5） 对角线互相垂直平分且相等的四边形是正方形.‎ 师生共析：‎ （1） 是真命题，.因为四条边相等的四边形是菱形，又四个角相等，根据四边形内角和定理知每个角为90°，所以由有一个角是直角的菱形是正方形可以判定此命题是真命题.‎ （2） 真命题，由.四个角相等可知每个角都是直角，是矩形，由对角线互相垂直可判定这个矩形是菱形，所以根据是矩形又是菱形的四边形是正方形，可判定其为真.‎ （3） 假命题，对角线平分的四边形是平行四边形，对角线垂直的四边形是菱形，所以它不一定是正方形.如下图，满足AO=CO，BO=DO且AC⊥BD但四边形ABCD不是正方形.‎ ‎ ‎ （4） 假命题，它可能是任意四边形.如上图，AC⊥BD且AC=BD，但四边形ABCD不是正方形.‎ （5） 真命题。‎ 方法一：对角线互相平分的四边形是平行四边形，对角线相等的平行四边形是矩形，对角线垂直的平行四边形是菱形，所以是矩形又是菱形的四边形是正方形.可判定其为真.‎ 菱 形 方法二：对角线平分 平行四边形 正方形 ‎ 对角线垂直 矩 形 ‎ 平行四边形 ‎ 对角线相等 ‎ ‎ 方法三：由对角线互相垂直平分可知是菱形，由对角线平分且相等可知是矩形，而既是菱形又是矩形的四边形就是正方形.‎ 总结：通过辨析，掌握判定正方形的各种方法和思路，从题中所给各种不同条件出发，寻找命题成立的判定依据，以便灵活应用.‎ ‎【补充例题】如下图，E、F分别在正方形ABCD的边BC、CD上，且∠EAF=45°，试说明EF=BE+DF.‎ 师生共析：要证EF=BE+DF，如果能将DF移到EB延长线或将BE移到FD延长线上，然后就能证明两线段长度相等。此时可依靠全等三角形来解决.‎ 像这种在EB上补上DF或在FD补上BE的方法叫做补短法.‎ 3‎ 解：将△ADF旋转到△ABC，则△ADF≌△ABG ‎∴AF=AG，∠ADF=∠BAG，DF=BG ‎∵∠EAF=45°且四边形是正方形， ‎ ‎∴∠ADF﹢∠BAE=45°，‎ ‎∴∠GAB﹢∠BAE=45°，‎ 即∠GAE=45°，‎ ‎∴△AEF≌△AEG（SAS），‎ ‎∴EF=EG=EB﹢BG=EB﹢DF。‎ 讨论：你能从一张彩色纸中剪出一个正方形吗？说出你的做法.‎ 你怎么检验它是一个正方形呢？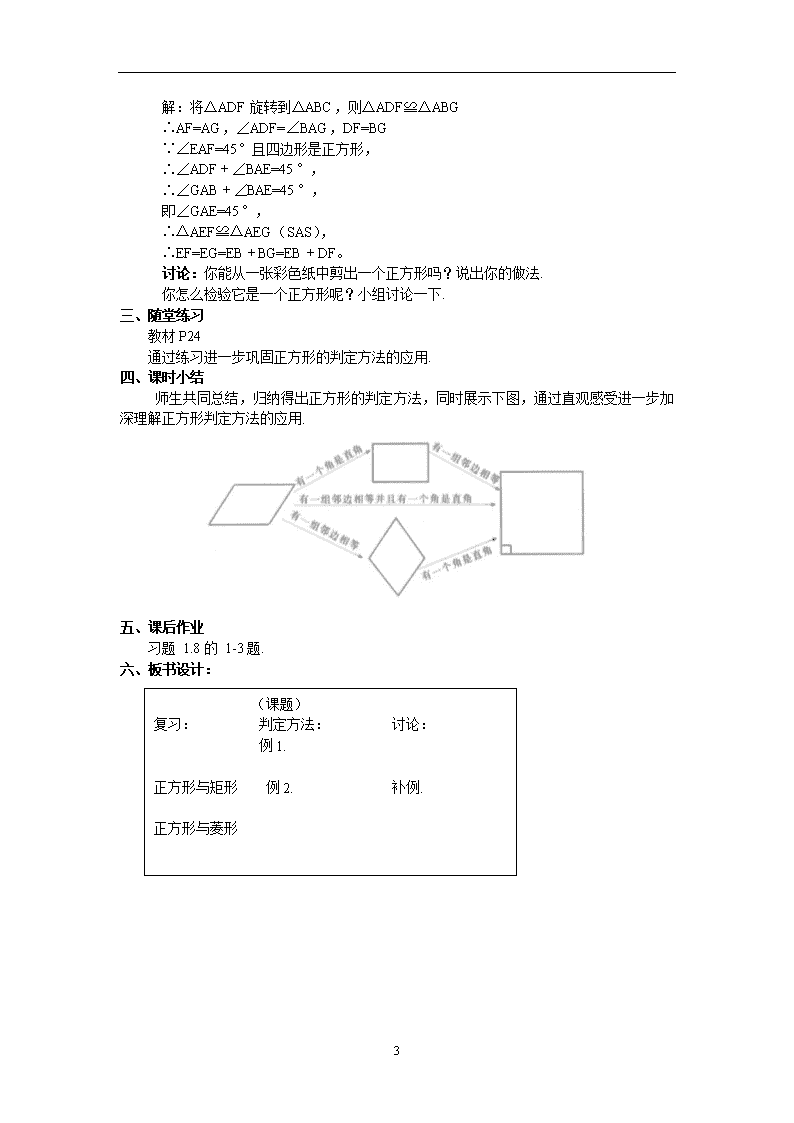小组讨论一下.‎ 三、随堂练习 ‎ 教材P24‎ 通过练习进一步巩固正方形的判定方法的应用.‎ 四、课时小结 师生共同总结，归纳得出正方形的判定方法，同时展示下图，通过直观感受进一步加深理解正方形判定方法的应用.‎ 五、课后作业 习题 1.8的 1-3题.‎ 六、板书设计：‎ ‎ （课题）‎ 复习： 判定方法： 讨论：‎ ‎ 例1. ‎ 正方形与矩形 例2. 补例.‎ 正方形与菱形 3‎