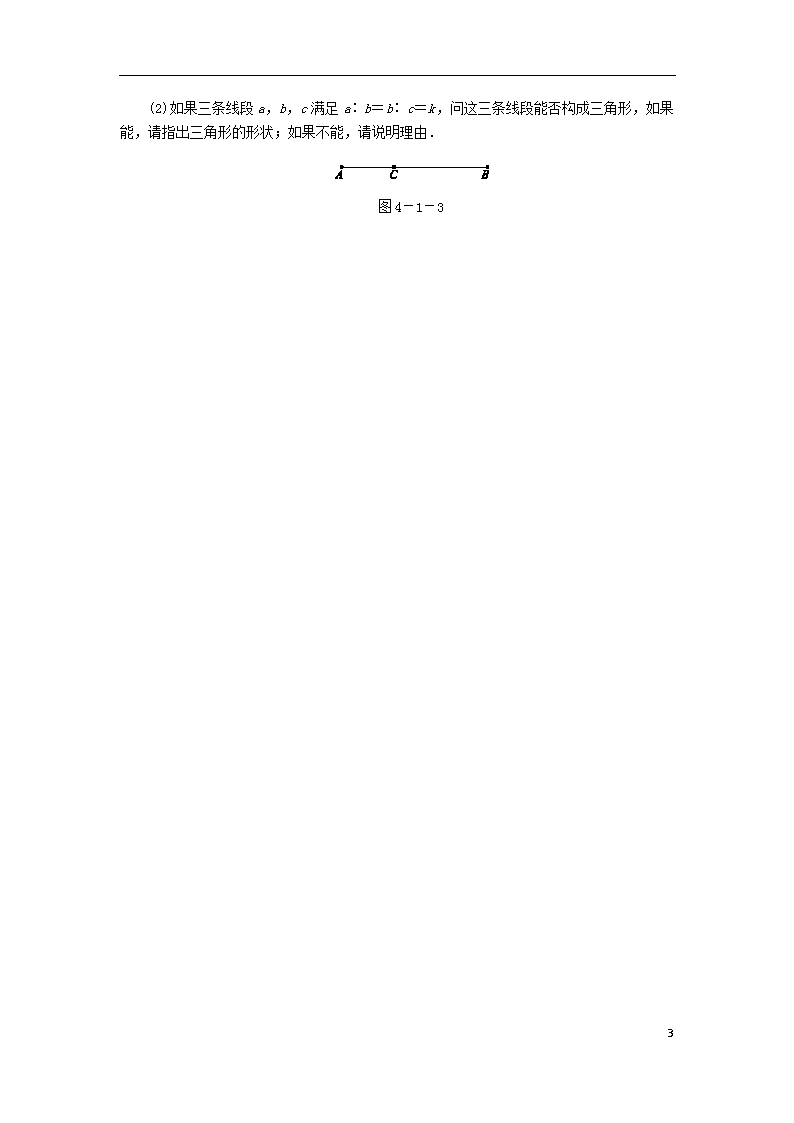2020年秋九年级数学上册 第4章相似三角形 5页

1 第 4 章　　相似三角形 4．1　比例线段 第 2 课时　比例线段 知识点 1　线段的比 1．正方形的边长与对角线的比是________． 2．下列说法中错误的是(　　) A．线段的比就是它们的长度之比 B．只要两条线段的长度采用同一单位，那么两条线段的比与所采用的单位无关 C．求两条线段的比，一定要用同一单位，如果单位不同，应先化成同一单位，再求它 们的比 D．两条线段的比与两个数的比一样有正有负 3．一根旗杆高 6 m，在正午的阳光下，其影长为 80 cm，则旗杆的高与它的影子的长度 之比为(　　) A. 3 40 B. 40 30 C. 2 15 D. 15 2 知识点 2　成比例线段 4．长度分别是 2cm，0.4cm，5cm，1cm 的四条线段________成比例线段(填“是”或“不 是”)． 5．已知△ABC 与△DEF 在网格中的位置如图 4－1－1 所示，每个小正方形的边长都是 1. (1)求 AB DE， BC EF， AC DF的值； (2)在 AB，BC，AC，DE，EF，DF 这六条线段中，指出其中三组成比例的线段． 图 4－1－1 2 知识点 3　比例尺 6．已知 A，B 两地的实际距离 AB＝5000 m，画在地图上的距离是 2 cm，则这张地图的比 例尺是(　　) A．2∶5 B．1∶25000 C．25000∶1 D．1∶250000 7．在一张比例尺为 1∶4000000 的地图上，杭州到嘉兴的图上距离约是 2cm，则杭州到 嘉兴的实际距离约为________km. 8．已知在△ABC 和△A′B′C′中， AB A′B′＝ BC B′C′＝ AC A′C′＝ 3 2，A′B′＋B′C′＋ A′C′＝16 cm，则 AB＋BC＋AC＝(　　) A．48 cm B．24 cm C．18 cm D．36 cm 9．已知四条线段 a，b，c，d 能组成比例线段，且 a＝14 cm，b＝16 cm，c＝13 cm，则 d＝_______________________. 10．如图 4－1－2 所示，已知 AD，CE 分别是△ABC 中 BC，AB 边上的高．求证：AD∶CE ＝AB∶BC. 图 4－1－2 11．如图 4－1－3，在线段 AB 上存在一点 C，满足 AC∶CB＝CB∶AB＝k. (1)求 k 的值． 3 (2)如果三条线段 a，b，c 满足 a∶b＝b∶c＝k，问这三条线段能否构成三角形，如果 能，请指出三角形的形状；如果不能，请说明理由． 图 4－1－3 4 详解详析 1．1∶ 2　[解析] 设正方形的边长为 1，则其对角线长为 2，故两者之比为 1∶ 2. 2．D　[解析] 线段的长不可能为负数． 3．D　[解析] 6 m＝600 cm， 600 80 ＝ 15 2 . 4．是　[解析] 2∶0.4＝20∶4＝5∶1. 5．解：(1)∵AB＝4 2，BC＝6，AC＝2 5，DE＝2 2，EF＝3，DF＝ 5， ∴ AB DE＝2， BC EF＝2， AC DF＝2. (2) AB DE＝ BC EF，AB，DE，BC，EF 是成比例线段； AB DE＝ AC DF，AB，DE，AC，DF 是成比例线段； BC EF＝ AC DF，BC，EF，AC，DF 是成比例线段． 6．D 7．80 　[解析] 杭州到嘉兴的图上距离约是 2 cm， 2×4000000＝8000000(cm)＝80 km. 8．B　[解析] ∵AB＝ 3 2A′B′，BC＝ 3 2B′C′，AC＝ 3 2A′C′，∴AB＋BC＋AC＝ 3 2(A′B′ ＋B′C′＋A′C′)＝ 3 2×16＝24(cm)． 9． 224 13 cm 或 91 8 cm 或 104 7 cm [解析] 此题答案不唯一，由题意，可列出下面的等式： ab＝cd 或 ac＝bd 或 ad＝bc， 所以可求得 d 的值为 224 13 或 91 8 或 104 7 . 10．证明：由三角形的面积公式得 5 1 2AB·CE＝ 1 2BC·AD， ∴AB·CE＝BC·AD， ∴AD∶CE＝AB∶BC. 11．解：(1)∵AC∶CB＝CB∶AB＝k， 若设 AB＝1，则 CB＝k，AC＝k2. 又∵AC＋CB＝AB， ∴k2＋k＝1，∴k＝ －1 ± 5 2 . 又∵k＞0，∴k＝ 5－1 2 . (2)线段 a，b，c 不能构成三角形． 理由：∵a∶b＝b∶c＝k， ∴b＝kc＝ 5－1 2 c，a＝kb＝( 5－1 2 )2c＝ 3－ 5 2 c， ∴a＋b＝c，∴线段 a，b，c 不能构成三角形．