九年级数学下册第二章二次函数2结识抛物线习题课件北师大版 28页

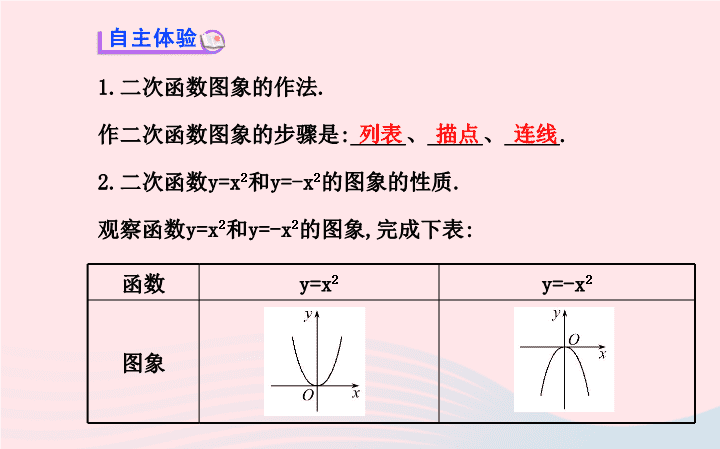
2 结识抛物线 1. 能利用描点法作出函数 y=x 2 的图象 , 能根据图象认识和理解二次函数 y=x 2 的性质 .( 重点、难点 ) 2. 能作出二次函数 y=-x 2 的图象 , 并能比较它与 y=x 2 图象的异同 .( 难点 ) 函数 y=x 2 y=-x 2 图象 1. 二次函数图象的作法 . 作二次函数图象的步骤是 :_____ 、 _____ 、 _____. 2. 二次函数 y=x 2 和 y=-x 2 的图象的性质 . 观察函数 y=x 2 和 y=-x 2 的图象 , 完成下表 : 列表 描点 连线 函数 y=x 2 y=-x 2 开口方向 _____ _____ 顶点坐标 ______ ______ 对称轴 y 轴 y 轴 函数变化 当 x>0 时 ,y 随 x 的增大而 _____; 当 x<0 时 ,y 随 x 的增大而 _____ 当 x>0 时 ,y 随 x 的增大而 _____; 当 x<0 时 ,y 随 x 的增大而 _____ 最大 ( 小 ) 值 当 x=0 时 ,y 最 __ 值 =0 当 x=0 时 ,y 最 __ 值 =0 向上 向下 (0,0) (0,0) 增大 减小 减小 增大 小 大 ( 打 “ √ ” 或 “ × ” ) (1) 二次函数 y=x 2 的图象与 x 轴没有交点 .( ) (2) 二次函数 y=x 2 的图象与 y=-x 2 的图象关于 x 轴对称 .( ) (3) 二次函数 y=-x 2 有最小值 .( ) (4) 点 (-2,4) 在二次函数 y=-x 2 的图象上 .( ) × √ × × 知识点 1 二次函数 y=x 2 和 y=-x 2 的性质   【 例 1】 已知点 (-2,y 1 ),(-2.5,y 2 ),(-0.5,y 3 ) 都在函数 y=-x 2 的图象上 , 试比较 y 1 ,y 2 ,y 3 的大小 . 【 教你解题 】 【 总结提升 】 比较 y=x 2 和 y=-x 2 的图象上若干个点的纵坐标的大小的 “ 三个步骤 ” 1. 比大小 : 比较各点横坐标及 0 之间的大小关系 . 2. 定位置 : 确定这些点是在对称轴的左边还是右边 . 3. 下结论 : 根据 y=x 2 或 y=-x 2 的增减性确定各点纵坐标的大小 . 知识点 2 y=x 2 和 y=-x 2 图象的应用   【 例 2】 如图 , 梯形 ABCD 是农民李伯 伯种植的一块无公害蔬菜地示意图 , 其顶点都在抛物线 y=-x 2 上 , 且 AB∥ CD∥x 轴 ,A 点坐标为 (a,-4),C 点坐标 为 (3,b), 请你帮助李伯伯计算这块菜 地的面积 ( 单位 : 米 2 ). 【 思路点拨 】 先求出 A,C 两点的坐标 , 再根据对称性求得 B,D 两 点的坐标 , 即可求得梯形的面积 . 【 自主解答 】 把 (a,-4) 代入 y=-x 2 , 得 -a 2 =-4, ∵a<0,∴a=-2, ∴A 点的坐标为 (-2,-4), 把 (3,b) 代入 y=-x 2 , 得 b=-9, ∴C 点的坐标为 (3,-9), 又∵ AB∥CD∥x 轴 , ∴A 与 B,C 与 D 分别关于 y 轴对称 , ∴B 点的坐标为 (2,-4),D 点的坐标为 (-3,-9). ∴AB=|-2-2|=4( 米 ),CD=|-3-3|=6( 米 ). 设梯形的高为 h, 则 h=|-4- （ -9 ） |=5( 米 ), ( 米 2 ), ∴ 这块菜地的面积为 25 米 2 . 【 总结提升 】 利用二次函数图象解题 1. 两种思想 : (1) 数形结合的思想 . (2) 转化的思想 , 能把实际问题转化为数学问题 . 2. 两点注意 : (1) 要注意线段的长度与点的坐标之间的转化 . (2) 在实际问题中函数的图象往往不是一条完整的抛物线 , 而是抛物线的一部分 . 题组一 : 二次函数 y=x 2 和 y=-x 2 的性质 1. 下列函数中 , 当 x<0 时 , 函数值 y 随 x 的增大而增大的有 ( 　　 ) ①y=3x,②y=-x+3,③ ④y=-x 2 . A.1 个 B.2 个 C.3 个 D.4 个 【 解析 】 选 C. 当 x<0 时 , 函数值 y 随 x 的增大而增大的是①③④ , 函数值 y 随 x 的增大而减小的是② , 所以函数值 y 随 x 的增大而增大的有 3 个 . 2. 关于抛物线 y=x 2 的性质错误的是　 ( 　　 ) A. 经过点 (-2,4) B. 对称轴是 y 轴 C. 与抛物线 y=-x 2 的开口大小一样 D. 与 y 轴不相交 【 解析 】 选 D.∵ 当 x=-2 时 ,y=4,∴ 抛物线经过点 (-2,4),∴A 选项正确 .∵a=1>0,∴ 抛物线的对称轴是 y 轴 , 与 y 轴交于点 (0,0), 与抛物线 y=-x 2 的开口大小一样 ,∴ 选项 B,C 正确 ,D 选项错误 . 3. 若点 A(2,a) 是抛物线 y=-x 2 上一点 , 则 a= 　　　　 . 【 解析 】 把 x=2,y=a 代入 y=-x 2 , 得 a=-4. 答案 : -4 【 变式备选 】 若点 A(b ， 2) 是抛物线 y=x 2 上一点，则 b=____ ． 【 解析 】 把 x ＝ b ， y ＝ 2 代入 y ＝ x 2 ，得 答案： 4. 已知点 (m,y 1 ),(m+3,y 2 ) 都在抛物线 y=x 2 上 , 且 m<-3, 则 y 1 　　　　 y 2 ( 填 “ > ”“ < ” 或 “ = ” ). 【 解析 】 ∵m<-3,∴my 2 . 答案 : > 5. 已知函数 是关于 x 的二次函数 . (1) 求满足条件的 m 的值 . (2)m 为何值时 , 抛物线有最低点？求出这个最低点 , 当 x 为何 值时 ,y 随 x 的增大而增大？ 【 解析 】 (1) 由题意得 , ∴ 当 m=0 或 m=2 时原函数为二次函数 . (2) 当 m=2 时 ,y=x 2 , 抛物线有最低点 , 这个最低点为抛物线的顶 点 , 其坐标为 (0,0), 当 x ＞ 0 时 ,y 随 x 的增大而增大 . 题组二： y=x 2 和 y=-x 2 图象的应用 1. 二次函数 y=x 2 与一次函数 在同一坐标系中的大致 图象为 ( ) 【 解析 】 选 A ． y=x 2 的图象开口向上，一次函数 的 图象经过第二、三、四象限，故选 A ． 2. 已知点 在二次函数 y=-x 2 的图象上，那么在二次函 数 y=-x 2 的图象上与点 A 对称的点 B 的坐标是 ______. 【 解析 】 把 代入 y ＝ -x 2 ，得 ∴点 A 的坐标为 又∵抛物线关于 y 轴对称， ∴点 B 的坐标是 答案： 3. 直线 y=x-6 与抛物线 y=-x 2 的交点坐标是 ______. 【 解析 】 由题意得 解得 或 ∴直线 y=x-6 与抛物线 y=-x 2 的交点坐标是 (-3 ， -9) 和 (2 ， -4) ． 答案： (-3 ， -9) 和 (2 ， -4) 【 名师点拨 】 求两个函数图象的交点的方法 　　两个函数图象的交点 , 是它们的公共点 , 这个点的横、纵坐标同时对应两个函数表达式中的两个变量 x,y. 因此 , 求两个函数图象的交点 , 就是求这两个函数表达式所组成的方程组的解 . 4. 如图 , 直线 l 经过 A(-2,0) 和 B(0,2) 两点 , 它与抛物线 y=x 2 在第二象限内相交于点 P, 求△ AOP 的面积 . 【 解析 】 设直线 l 的关系式为 y=kx+b(k,b 为常数 ,k≠0), 则有： ∴ y=x+2, 由题意 , 得 ∵点 P 在第二象限 , ∴ 点 P 的坐标是 (-1,1), 【 想一想错在哪？ 】 作出函数 y=x 2 的图象 . 提示 : (1) 列表应体现点可取无数个 . (2) 画二次函数图象时 , 要用平滑的曲线连接相邻的点 . (3) 图象应向上 ( 或下 ) 伸出 “ 头 ” .