九年级数学上册第四章图形的相似6利用相似三角形测高习题课件新版北师大版 10页

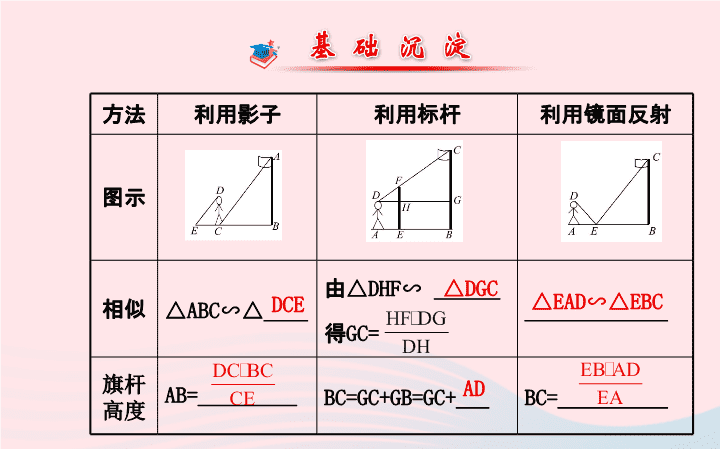
6 　 利用相似三角形测高 方法 利用影子 利用标杆 利用镜面反射 图示 相似 △ABC∽△____ 由△ DHF∽ ______ 得 GC= _____________ 旗杆高度 AB=_________ BC=GC+GB=GC+___ BC=__________ DCE △DGC △EAD∽△EBC AD 【 思维诊断 】 ( 打“√”或“ ×”) 1. 用标杆测量时 , 眼睛必须和标杆的顶端、被测物体顶端共 线 . 　 ( ) 2. 在阳光下 , 两个物体的长度与影长成正比 . 　 ( ) 3. 在灯光下 , 不同的物体的影长也有可能相同 . 　 ( ) 4. 利用镜面反射测量物体的高度时 , 不必遵循平面镜的反射定律 . 　 ( ) √ × √ × 知识点 应用相似三角形测量物体的高度 【 示范题 】 某同学想测量旗杆的高度 , 他在某一 时刻测得 1m 长的竹竿竖直时影长为 1.5m. 在同一 时刻测量旗杆的影长时 , 因旗杆靠近一幢楼房 , 影 子不全落在地面上 , 有一部分落在墙上 , 他测得落在地面上的影长为 21m, 留在墙上的影子为 2m, 你能帮助他求出旗杆的高度吗 ? 【 思路点拨 】 根据太阳光下某一时刻 , 物高与影长成正比 , 只需要求出落在地面上的 21m 长的影长是旗杆的哪一部分形成的即可 . 过点 C 作 CE∥BD, 交 AB 于点 E. 【 自主解答 】 过点 C 作 CE∥BD, 交 AB 于点 E, 得四边形 BDCE 是矩形 , 则 BE=CD=2m,CE=BD=21m. 设 AE=x, 根据题意得 即 解得 x=14, 所以旗杆的高度为 14+2=16(m). 【 想一想 】 除例题解法外 , 还有其他方法吗 ? 提示 : 延长 BD 交 AC 的延长线于点 F, 先求得 DF, 然后得旗杆的影长 , 最后根据比例式解之 . 【 备选例题 】 如图 , 有一路灯杆 AB( 底部 B 不能直接到达 ), 在灯光下 , 小明在点 D 处测得自己的影长 DF=3m, 沿 BD 方向到达点 F 处再测得自己的影长 FG=4m, 如果小明的身高为 1.6m, 求路灯杆 AB 的高度 . 【 解析 】 因为 CD∥EF∥AB, 所以可以得到△ CDF∽△ABF,△EFG∽△ABG, 所以 又因为 CD=EF, 所以 因为 DF=3,FG=4,BF=BD+DF=BD+3, BG=BD+DF+FG=BD+7, 所以 所以 BD=9m,BF=9+3=12(m), 所以 解得 ,AB=6.4m. 【 方法一点通 】 利用相似三角形测量物体高度的一般步骤 1. 画出示意图 , 利用平行光线、影子、标杆等构造相似三角形 . 2. 测量与表示未知量的线段相对应的边长 , 以及另外一组对应边的长度 . 3. 利用相似三角形的性质列出包括以上四个量的比例式 , 求出未知量 . 4. 检验并得到答案 .