2019九年级数学上册 第二十四章正多边形和圆 6页

正多边形和圆 教学设计 课 标 要 求 ‎ ‎ ‎ 利用正多边形解决有关问题 教 材 及 学 情 分 ‎ 析 1、 ‎ 教材分析：‎ ‎ 学生在学习本章之前，已通过折叠、对称、平移、旋转、推理证明等方式认识了许多图形的性质，积累了大量的空间与图形的经验．本章是在学习了这些直线型图形的有关性质的基础上，进一步来探索一种特殊的曲线──圆的有关性质．通过本章的学习，对学生今后继续学习数学，尤其是逐步树立分类讨论的数学思想、归纳的数学思想起着良好的铺垫作用．本章的学习是高中的数学学习，尤其是圆锥曲线的学习的基础性工程．‎ 学情分析：‎ ‎ 2、九年级学生已具备一定知识储备和认知能力。但学生的基础较差，中等、差等生较多，优等生较少。课堂上，多数学生表现欲不强，发言不积极，怕回答错问题；学生应用知识灵活解决问题的能力较差，在几何证明题中，不会抓住已知条件进行论证推理。因此，在教学中，注重学生学习方法的培养，通过学生实践、探究、合作交流来完成本节课的教学。‎ 课 时 教 学 目 标 ‎1．理解正多边形的性质．‎ ‎2．会画正多边形，了解依次连结圆的n等分点所得的多边形是正多边形，过圆的n等分点作圆的切线，以相邻切线的交点为顶点的多边形是正多边形．‎ 重点 正多边形的画法．‎ 难点 对正n边形中泛指“n”的理解．‎ 教法学法 指导 ‎ 合作探究法 引导启发法 练习法 教具 ‎ 课件 6‎ 准备 教学过程提要 环节 学生要解决的问 题或完成的任务 师生活动 设计意图 引 入 新 课 一、 复习旧知：‎ 二、探究正多边形的画法 一、复习：‎ ‎1、什么是正多边形?怎么证明一个多边形是正多边形？‎ ‎2、多边形的内角和怎么计算？正多边形的每一个内角怎么计算？‎ ‎3、复习正多边形的相关概念;正多边形的中心角怎么计算？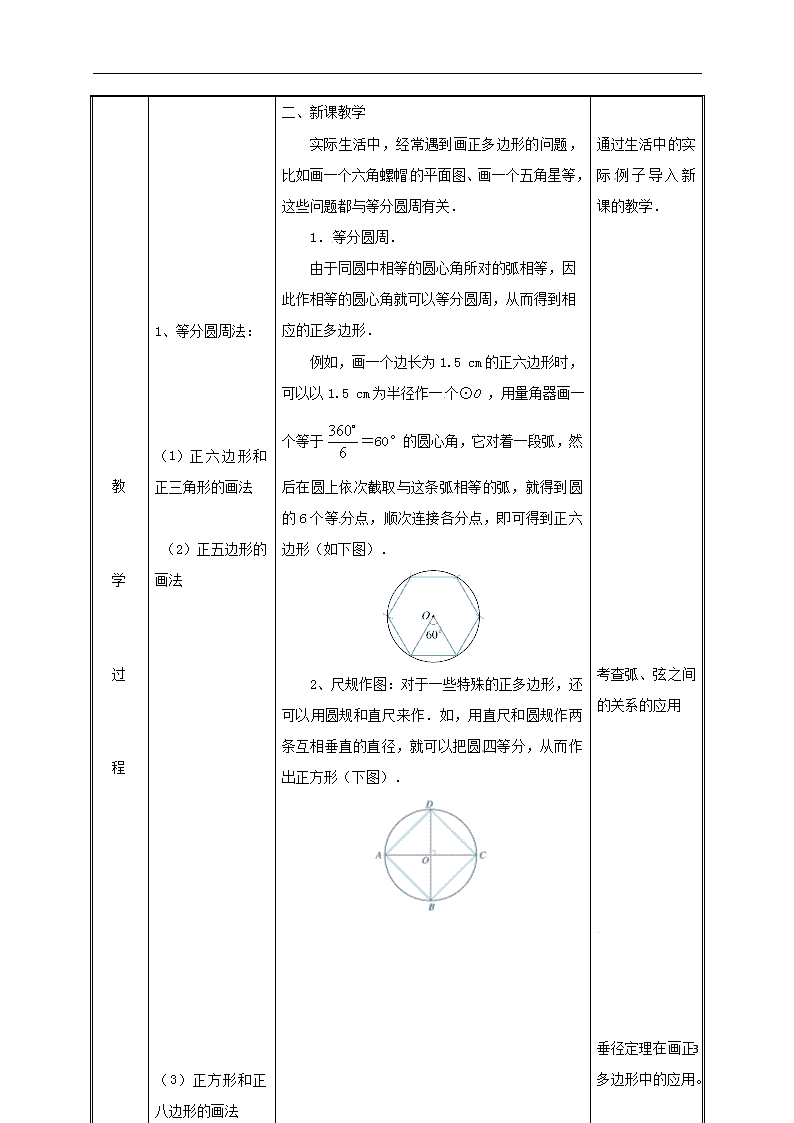‎ ‎ ‎ ‎ 巩固上节课所学的内容 6‎ 教 学 过 程 ‎1、等分圆周法：‎ （1） 正六边形和正三角形的画法 ‎ ‎ ‎ （2）正五边形的画法 ‎（3）正方形和正八边形的画法 二、新课教学 实际生活中，经常遇到画正多边形的问题，比如画一个六角螺帽的平面图、画一个五角星等，这些问题都与等分圆周有关．‎ ‎1．等分圆周．‎ 由于同圆中相等的圆心角所对的弧相等，因此作相等的圆心角就可以等分圆周，从而得到相应的正多边形．‎ 例如，画一个边长为‎1.5 cm的正六边形时，可以以‎1.5 cm为半径作一个⊙O ，用量角器画一个等于＝60°的圆心角，它对着一段弧，然后在圆上依次截取与这条弧相等的弧，就得到圆的6个等分点，顺次连接各分点，即可得到正六边形（如下图）．‎ ‎2、尺规作图：对于一些特殊的正多边形，还可以用圆规和直尺来作．如，用直尺和圆规作两条互相垂直的直径，就可以把圆四等分，从而作出正方形（下图）．‎ ‎ ‎ 通过生活中的实际例子导入新课的教学．‎ 考查弧、弦之间的关系的应用 垂径定理在画正多边形中的应用。‎ 6‎ 教 学 过 程 三、正多边形画法的应用 三、巩固练习 ‎3．实例探究．‎ 用等分圆周的方法画出下列图案．‎ 提示：第1幅图案．以圆的三等分点为圆心，圆的半径为半径作三条弧．‎ 第2幅图案．以正六边形的各边中点为圆心，正六边形的边长为直径向圆外画半圆，就得到这幅图案．‎ 第3幅图案．作5的内接正五边形，再以正五边形的各个顶点为圆心，边长为半径画十条弧．‎ 4、 巩固练习：‎ ‎ 画一个半径为‎2cm的正五边形，再作出这个正五边形的各条对角线，画一个五角星。‎ 用画正多边形的画法实际美丽图案，感受生活中的数学美 巩固所学知识、会用新知解决问题 6‎ 小 结 ‎ 今天学习了什么？有哪些问题？‎ 板 书 设 计 ‎ 24.3 正多边形和圆 ‎1、正多边形：各边相等，各角相等的多边形叫做正多边形．‎ ‎2、正多边形的相关概念：‎ ‎ （1）中心 （2）半径 ‎ （3）中心角，（4）边心距 ‎3、正多边形的画法：（1）等分圆周；（2）尺规作图 作 业 设 计 绩优学案：p104页 ‎ 1、必做题：1——8题 ‎ 2、选做题：9题 6‎ 教 学 反 思 6‎