九年级数学下册第一章直角三角形的边角关系4船有触礁的危险吗课件北师大版 27页

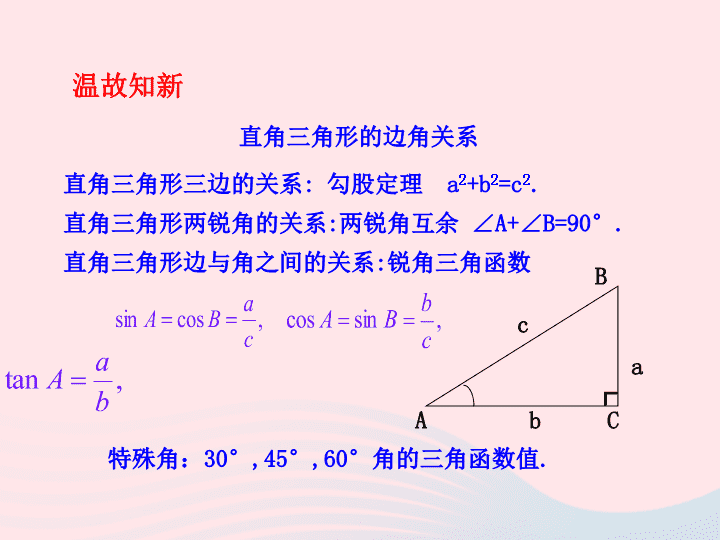
4 船有触礁的危险吗 1. 经历探索船是否有触礁危险的过程，进一步体会三角函数在解决问题过程中的应用 .2. 能够把实际问题转化为数学问题，能够借助于计算器进行有关三角函数的计算，并能对结果的意义进行说明 . 直角三角形两锐角的关系:两锐角互余 ∠A+∠B=9 0°. 直角三角形三边的关系: 勾股定理 a 2 +b 2 =c 2 . b A B C a ┌ c 直角三角形边与角之间的关系:锐角三角函数 直角三角形的边角关系 特殊角： 30°,45°,60° 角的三角函数值 . 温故知新 你认为货船继续向西航行途中会有触礁的危险吗 ? B 25º C 20 1. 审题，画图 . 大海中有一个小岛 A, 该岛四周 10 海里内有暗礁 . 今有货船由东向西航行 , 开始在 A 岛南偏东 55° 的 B 处 , 往西行驶 20 海里后到达该岛南偏东 25° 的 C 处之后 , 货船继续向西航行 . 55° 被观测点 A （参考数据： sin55º=0.819,cos55º=0.574,tan55º=1.428, sin25º=0.423,cos25º=0.906,tan25º=0.466) 北 D 观测点 探究一 B C 20 D A x 2. 确定已知和未知 . 3. 设适当的未知数，列方程 55º B D A x C D A x 25º 解： 根据题意可知，∠ BAD=55° ， ∠ CAD=25° ， BC= 20 海里 . 设 AD=x ，则 答 : 货轮继续向西航行途中没有触礁的危险 . 4. 解方程，结论 . 如图 , 小明想测量塔 CD 的高度 . 他在 A 处仰望塔顶 , 测得仰角为 30°, 再往塔的方向前进 50m 至 B 处 , 测得仰角为 60°, 那么该塔有多高 ?( 小明的身高忽略不计 , 结果精确到 1m). 请与同伴交流你是怎么想的，准备怎么去做 . 现在你能完成这个任务吗 ? 要解决这个问题 , 我们仍需将其数学化 . 探究二 D A B C ┌ 50m 30° 60° 答 : 该塔约有 43m 高 . 解 : 如图 , 根据题意可知 ,∠A=30°,∠DBC=60°, AB=50m. 设 CD=xm, 则∠ ADC=60°,∠BDC=30°, 某商场准备改善原有楼梯的安全性能 , 把倾角由原来的 40° 减至 35°, 已知原楼梯的长度为 4m, 调整后的楼梯会加长多少 ? 楼梯多占多长一段地面 ?( 结果精确到 0.01m). 现在你能完成这个题目吗 ? 请与同伴交流你是怎么想的， 准备怎么去做 . A B C D ┌ 探究三 解 : (1) 如图 , 根据题意可知 ,∠A=35°, ∠BDC=40°,DB=4m. A B C D ┌ 4m 35° 40° 答 : 调整后的楼梯会加长约 0.48m. (2) 如图 , 根据题意可知 ,∠A=35°,∠BDC=40°,DB=4m. 答 : 楼梯多占约 0.61m 长的一段地面 . A B C D ┌ 4m 35° 40° 如图 , 一灯柱 AB 被一钢缆 CD 固定 .CD 与地面成 40° 夹角 , 且 DB=5m. 现再在 C 点上方 2m 处加固另一条钢缆 ED, 那么 , 钢缆 ED 的长度为多少 ?( 结果精确到 0.01m). 探究四 解 : 如图 , 根据题意可知 ,∠CDB=40°,EC=2m, DB=5m. ∴∠BDE≈51.12°. E B C D 2m 40° 5m 答 : 钢缆 ED 的长度约为 7.97m. 如图 , 水库大坝的截面是梯形 ABCD, 坝顶 AD=6m, 坡长 CD=8m. 坡底 BC=30m,∠ADC=135°. (1) 求∠ ABC 的大小（精确到 1° ） ; (2) 如果坝长 100m, 那么修建这个大坝共需多少土石 ( 结果精确到 0.01m 3 ). A B C D 探究五 A B C D 6m 8m 30m 135° 解： （ 1 ） 过点 D 作 DE⊥BC 于点 E, 过点 A 作 AF⊥BC 于点 F. E ┐ F ┌ ∴∠ABC≈17°. 答 :∠ABC 约为 17°. （ 2 ） 再求体积 ! 先算面积 ! 答 : 修建这个大坝共需土石约 10182.34m 3 . 100m A B C D 6m 8m 30m 135° E ┐ F ┌ 1. （株洲 · 中考）如图，孔明同学背着一桶水，从山脚 A 出发，沿与地面成 30° 角的山坡向上走，送水到山上因今年春季受旱缺水的王奶奶家（ B 处）， AB=80 米，则孔明从 A 到 B 上升的高度 BC 是 米． 【 解析 】 依题意得，∠ ACB=90°. 所以 sin A =sin30°= ，所以 BC=40 （米） . 答案： 40 30° 2. （衡阳 · 中考）为申办冬奥会，须改变哈尔滨市的交通状况 . 在大直街拓宽工程中，要伐掉一棵树 AB ，在地面上事先划定以 B 为圆心，半径与 AB 等长的圆形危险区，现在某工人站在离 B 点 3 米远的 D 处，从 C 点测得树的顶端 A 点的仰角为 60° ，树的底部 B 点的俯角为 30°. 问：距离 B 点 8 米远的保护物是否在危险区内？ 【 解析 】 在 Rt△BDC 中， BC= =2 所以离 B 点 8 米远的保护物不在危险区内 . 在 Rt△ABC 中， AB=2BC=4 ＜ 8 ， 3. （湘潭 · 中考）如图，我护航军舰在某海域航行到 B 处时，灯塔 A 在我军舰的北偏东 60 o 的方向；我军舰从 B 处向正东方向行驶 1 800 米到达 C 处，此时灯塔 A 在我军舰的正北方向．求 C 处与灯塔 A 的距离（结果保留四个有效数字）． 东 北 60 o A C B 【 解析 】 在 Rt△ABC 中，∠ C=90 ° ， BC=1800 ，∠ ABC=30 ° ， 答： C 处与灯塔 A 的距离约为 1039 米． 从而 =600 ≈1 039. 东 北 60 o A C B 4. （鄂州 · 中考）如图，一艘舰艇在海面下 500 米 A 点处测得俯角为 30° 前下方的海底 C 处有黑匣子信号发出，继续在同一深度直线航行 4 000 米后再次在 B 点处测得俯角为 60° 前下方的海底 C 处有黑匣子信号发出，求海底黑匣子 C 点距离海面的深度（结果保留根号）． 【 解析 】 作 CF 垂直于 AB 延长线于点 F ，则 ∴ ∵ ∴ ∴ ∴ 海底黑匣子 C 点距离海面的深度为 5 ．（贵阳 · 中考）某商场为缓解我市“停车难”问题，拟建造地下停车库，如图是该地下停车库坡道入口的设计示意图，其中， AB⊥BD ，∠ BAD ＝ 18° ，点 C 在 BD 上， BC ＝ 0.5m ．根据规定，地下停车库坡道入口上方要张贴限高标志，以便告知驾驶员所驾车辆能否安全驶入．小明认为 CD 的长就是所限制的高度，而小亮认为应该以 CE 的长作为限制的高度．小明和小亮谁说的对？请你判断并计算出正确的结果 . （结果精确到 0.1m ） 【 解析 】 小亮说的对，在△ ABD 中，∠ ABD ＝ 90° ， ∠ BAD ＝ 18 ° ， BA ＝ 10 ， ∴tan∠BAD ＝ ∴BD ＝ 10×tan 18° ， 在 CDE 中，∠ CDE ＝ 90 ° ―∠BAD ＝ 72° ， ∵CE⊥ED∴sin∠CDE ＝ ∴CD ＝ BD―BC ＝ 10×tan 18° ―0.5 ， ―0.5 ）≈ 2.6 （ m ） ∴CE ＝ CD×sin∠CDE ＝ sin72 °× （ 10×tan 18° 答： CE 为 2.6m ，即限制高度为 2.6m. 【 规律方法 】 根据题意画出几何图形，构造直角三角形，灵活运用三角函数的定义结合勾股定理的有关知识是进行解题的关键 . 1. 审题，画图 . 2. 确定已知和未知 . 3. 设适当的未知数，列方程 . 4. 解方程，结论 . 解有关实际意义的应用题的一般步骤： 从来没有人读书，只有人在书中读自己，发现自己或检查自己 . —— 罗曼 · 罗兰