2020年秋苏科版 数学八年级上6.4用一次函数解决问题课后练习 11页

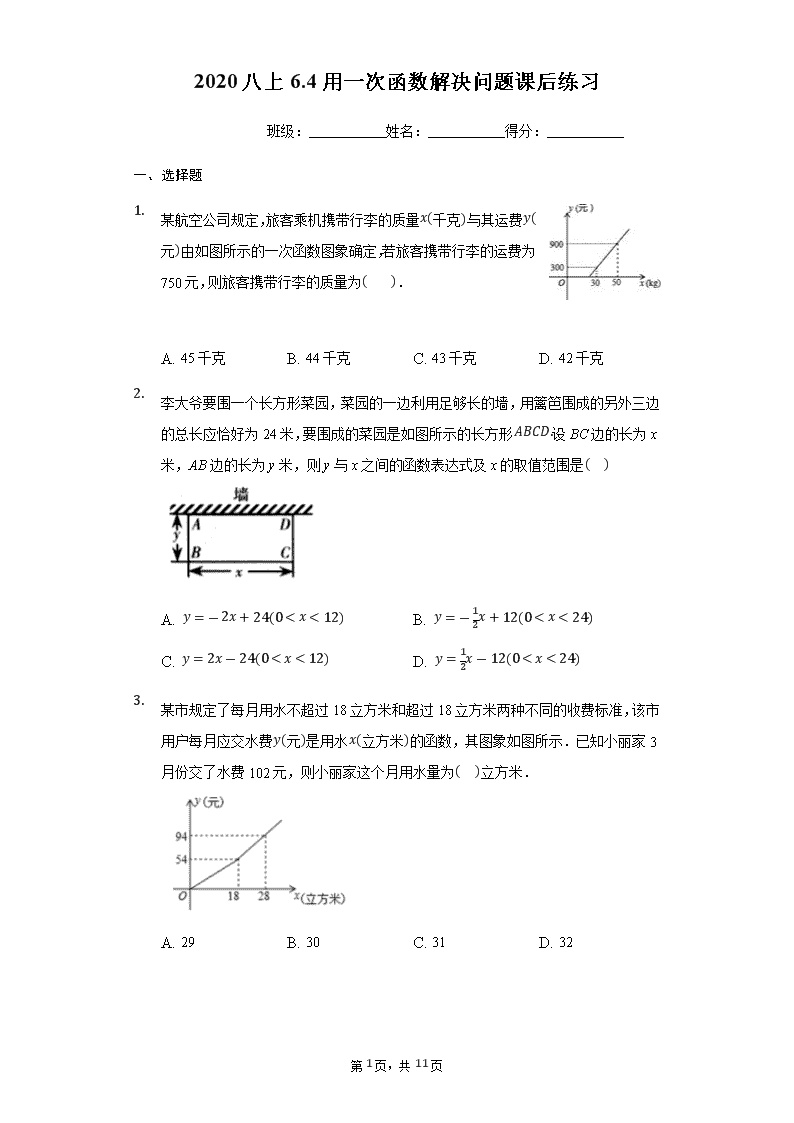
第 1 页，共 11 页 2020 八上 6.4 用一次函数解决问题课后练习 班级：___________姓名：___________得分：___________ 一、选择题 1. 某航空公司规定，旅客乘机携带行李的质量 千克 与其运费 元 由如图所示的一次函数图象确定，若旅客携带行李的运 费为 750 元，则旅客携带行李的质量为 ． A. 45 千克 B. 44 千克 C. 43 千克 D. 42 千克 2. 李大爷要围一个长方形菜园，菜园的一边利用足够长的墙，用篱笆围成的另外三边 的总长应恰好为 24 米，要围成的菜园是如图所示的长方形 ܤܥ. 设 BC 边的长为 x 米，AB 边的长为 y 米，则 y 与 x 之间的函数表达式及 x 的取值范围是 A. = − 2 + 2t < < 12 B. = − 1 2 + 12 < < 2t C. = 2 − 2t < < 12 D. = 1 2 − 12 < < 2t 3. 某市规定了每月用水不超过 18 立方米和超过 18 立方米两种不同的收费标准，该市 用户每月应交水费 元 是用水 立方米 的函数，其图象如图所示．已知小丽家 3 月份交了水费 102 元，则小丽家这个月用水量为 立方米． A. 29 B. 30 C. 31 D. 32 t. 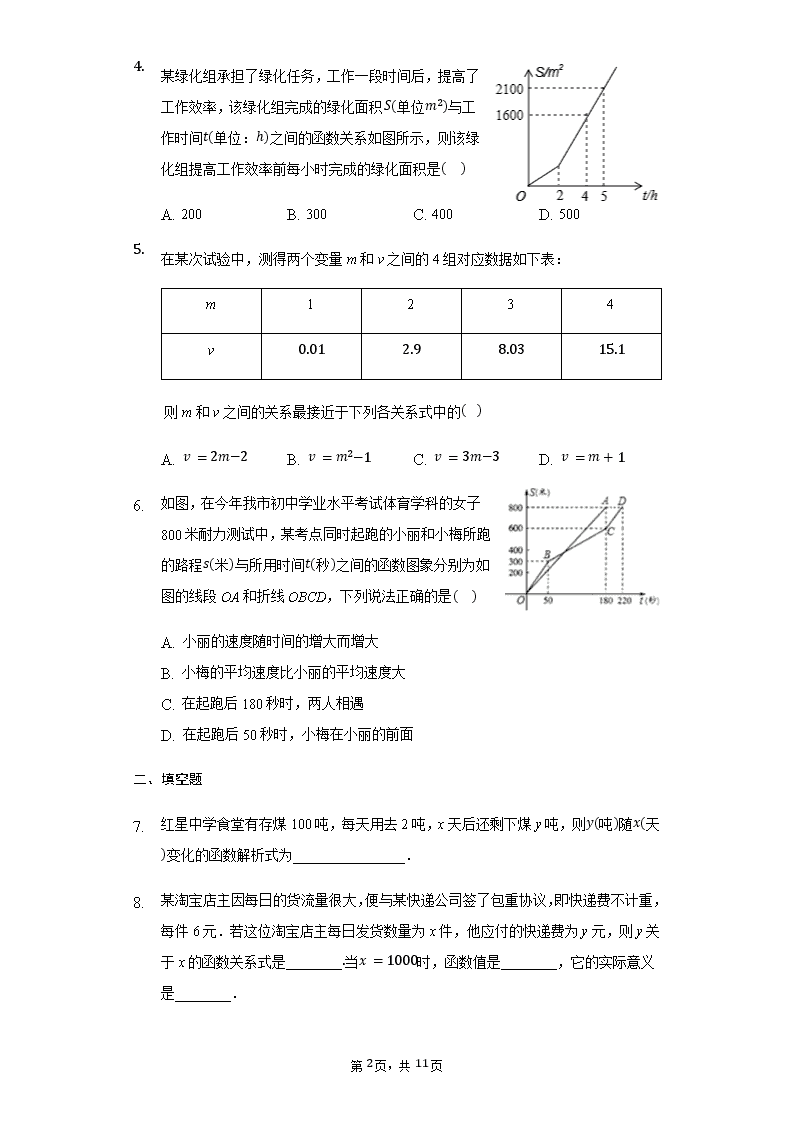某绿化组承担了绿化任务，工作一段时间后，提高了工作效率，该绿化组完成的绿 化面积 单位 2 与工作时间 单位： 之间的函数关系如图所示，则该绿化组提 第 2 页，共 11 页 高工作效率前每小时完成的绿化面积是 A. 200 B. 300 C. 400 5. 在某次试验中，测得两个变量 m 和 v 之间的 4 组对应 数据如下表： m 1 2 3 4 v .1 2.o .3 15.1 则 m 和 v 之间的关系最接近于下列各关系式中的 A. = 2 2 B. = 2 1 C. = 3 3 D. = + 1 6. 如图，在今年我市初中学业水平考试体育学科的女子 800 米耐力测试中，某考点同时起跑的小丽和小梅所跑 的路程 米 与所用时间 秒 之间的函数图象分别为 如图的线段 OA 和折线 OBCD，下列说法正确的是 A. 小丽的速度随时间的增大而增大 B. 小梅的平均速度比小丽的平均速度大 C. 在起跑后 180 秒时，两人相遇 D. 在起跑后 50 秒时，小梅在小丽的前面 二、填空题 7. 红星中学食堂有存煤 100 吨，每天用去 2 吨，x 天后还剩下煤 y 吨，则 吨 随 天 变化的函数解析式为________________． 8. 某淘宝店主因每日的货流量很大，便与某快递公司签了包重协议，即快递费不计重， 每件 6 元．若这位淘宝店主每日发货数量为 x 件，他应付的快递费为 y 元，则 y 关 于 x 的函数关系式是________ . 当 = 1 时，函数值是________，它的实际意义 是________． 9. 某通讯公司推出市话眼务，收费标准为月租费 25 元，本地网通话费为每分钟 .1元 不足 1 分钟按 1 分钟计算 ． 第 3 页，共 11 页 1 完成下表： 全月通话时间 分 1 2 3 4 当月通话费用 元 当月应缴费用 元 2 根据上表提供的信息，写出 y 与 x 的函数表达式：_______． 10. 在一次越野赛跑中，当小明跑了 1600 米时，小刚跑了 1400 米，小明、小刚在此后 所跑的路程 米 与时间 秒 之间的函数图象如图所示，根据图象可知再跑 ________秒，小刚就会追上小明． 11. 甲骑自行车从 A 地出发前往 B 地，同时乙步行从 B 地出发前往 A 地，如图的折线 OPQ 和线段 EF 分别表示甲、乙两人与 A 地的距离 甲、 乙与他们所行时间 之间的函数关系，且 OP 与 EF 相交于点 . 则经过______小时，甲、乙两人相距 3km． 12. 某市政府为了增强城镇居民抵御大病风险的能力，积极完善城镇居民医疗保险制度， 纳入医疗保险的居民大病住院医疗费用的报销比例标准如表： ．若租车时间为 8 小时，请你帮助小明计算选择哪个租车方案合算 2 关于 x 的函数表达式； 2 、 1 元，直． 接．写出 2 费用为 元，租用乙公司的车所需 1 设租车时间为 x 小时，租用甲公司的车所需费用为 1 出游．根据信息，解答下列问题： 13. “五一”期间，小明一家乘坐高铁前往某市旅游，计划第二天租用新能源汽车自驾 三、解答题 ________ ． 述标准报销后，该居民实际支出的金额为 y 元．则 y 关于 x 的函数关系式为 ，按上 < 3 设享受医保的某居民一年的大病住院医疗费用为 x 元，且 ؂ 超过 5000 元的部分 ؂ 超过 3000 元且不超过 5000 元的部分 ؂5 超过 800 元且不超过 3000 元的部分 不超过 800 元 不予报销 医疗费用范围 报销比例标准 页 11 页，共 t 第 第 5 页，共 11 页 14. 某移动公司有两类收费标准：A 类收费是不管通话时间多长，每部手机每月须缴月 租 12 元．另外，通话费按 .2 元 ㄠ㈴ ；B 类收费是没有月租，但通话费按 .25 元 ㄠ㈴ ． 1 请分别写出每月应缴费用 元 与通话时间 ㄠ㈴ 之间的关系式； 2 若小芳爸爸每月通话时间为 300min，请说明选择哪种收费方式更合算； 3 每月通话多长时间，按 A、B 两类收费标准缴费，所缴话费相等． 15. 如下图表示甲乙两船沿相同路线从 A 港出发到 B 港行驶过程中路随时间变化的图 象，根据图象解答下列问题： 1 分别求出两船行驶的速度； 2 请分别求出表示甲船和乙船行驶过程的函数解析式； 3 问乙船出发多长时间赶上甲船？ 第 页，共 11 页 16. 某星期天早晨，小华从家出发步行前往体育馆锻炼，途中在报亭看了一会儿报，如 图所示是小华从家到体育馆这一过程中所走的路程 米 与时间 分 之间的关系． 1 体育馆离小华家_______米，从出发到体育馆，小华共用了______分钟； 2 小华在报亭看报用了多少分钟？ 3 小华看完报后到体育馆的平均速度是多少？ 第 页，共 11 页 答案和解析 1. A 解：设 y 与 x 的函数关系式为 = +   ， 由题意可知： 3 = 3 +  Ͳ o = 3 +  Ͳ ， 解得： = 3Ͳ   = Ͳ ， 函数关系式为 = 3 ， 当 = 5 时，得 5 = 3 ， = t5 千克． 2. B 解：由题意得： 2 + = 2t ， 故可得： = − 1 2 + 12 < < 2t ． 3. B 解：设当 ： 1 时的函数解析式为 = +   ， 由图可知图像经过 1Ͳ5t ， 2Ͳot则可知超过 18 立方米每立方米水费 = ot5t 21 = t ， 将 2Ͳ5t 代入解析式可得 t 2 +   = ot ，解得   = 1即当 ： 1 时的函数解析式为 = t 1 ， 12 ： 5t ， 当 = 12 时， 12 = t 1 ，得 = 3 ， 4. B 第 页，共 11 页 解：从图象可以知 2 至 5 时的函数图象经过 tͲ15Ͳ21 ， 设该时段的一次函数解析式为 = +   2 ，依题意，将点 tͲ15Ͳ21 分别 代入， 可列方程组有 1 = t +   21 = 5 +   ，解得： = 5   = t ， 一次函数的解析式为： = 5 t ， 当 = 2 时，解得 = ， 前两小时每小时完成的绿化面积是 2 = 3 2 ， 5. B 解：当 = t 时， A. = 2 2 = ； B. = 2 1 = 15 ； C. = 3 3 = o ； D. = + 1 = 5 ． 6. D 解： . 由于线段 OA 表示所跑的路程 米 与所用时间 秒 之间的函数图象，由此可以 确定小丽的速度是没有变化的．故本选项错误； B.小丽比小梅先到，由此可以确定小梅的平均速度比小丽的平均速度小．故本选项错误； C.根据图象可以知道起跑后 180 秒时，两人的路程不相等，故没有相遇．故本选项错误； D.根据图象知道起跑后 50 秒时 OB 在 OA 的上面，可以确定小梅的路程比小丽的路程多， 所以小梅在小丽的前面．故本选项正确． 7. = 1 2 第 o 页，共 11 页 解：解：由题意得， = 1 2 ， 则 吨 随 天 变化的函数解析式为 = 1 2 ， 8. = ；6000；邮寄 1000 件物品所需费用为 6000 元 解：由题意可得 y 与 x 的函数关系式为 = ， 当 = 1 时，则 = ， 它的实际意义为邮寄 1000 件物品所需费用为 6000 元． 9. 1.1 ； .2 ； .3 ； .t ； 25.1 ； 25.2 ； 25.3 ； 25.t 2 = 25 + .1 解： 1 当通话时间为 1 分钟时，当月通话费用为 .1 元，当月应缴费用为 25 + .1 = 25.1 元 ； 当通话时间为 2 分钟时，当月通话费用为 .2 元，当月应缴费用为 25 + .2 = 25.2 元 ； 当通话时间为 3 分钟时，当月通话费用为 .3 元，当月应缴费用为 25 + .3 = 25.3 元 ； 当通话时间为 4 分钟时，当月通话费用为 .t 元，当月应缴费用为 25 + .t = 25.t 元 ； 故答案为 .1 ； .2 ； .3 ； .t ； 25.1 ； 25.2 ； 25.3 ； 25.t ； 2 由表格可得，y 与 x 的函数表达式为 = 25 + .1 ． 10. 100 解：由图象可得当 = 1 秒时，小刚会追上小明． 11. 3 或 5 解：设线段 OP 对应的 甲与 x 的函数关系式为 甲 = ， o = .5 ，得 = 1 ， 即线段 OP 对应的 甲与 x 的函数关系式为 甲 = 1 ； 设 乙与 x 的函数关系式为 乙 = ܽ +   ，则 第 1 页，共 11 页 .5ܽ +   = o 2ܽ +   = ， 得 ܽ =   = 12 ， 即 乙与 x 的函数关系式为 乙 = + 12 ， 当 = 时， 乙 = 12 ， 即 A，B 两地的距离是 12km， 当甲步行至乙地后，甲、乙两人相距必大于 3km， 甲、乙两人相距 3km 时有： + 12 1 = 3 ， 解得， 1 = 3 ， 2 = 5 ， 12. = .5 + t 解：当 < 3 时， = .5 = .5 + t ． 13. 解： 1 由题意可得： 1 = 15 + ， 2 = 3 ； 2 当 = 时， 1 = 15 + = 2 ， 2 = 3 = 2t ， 2 < 2t ， 选择方案一合算． 14. 解： 1 类： = .2 + 12 ， B 类： = .25 ； 2 类收费： 12 + .2 3 = 2 元； B 类收费： .25 3 = 5 元， 5 ： 2 ， 所以选择 A 类收费方式； 3 设每月通话时间 x 分钟， 由题意得 12 + .2 = .25 ， 解得： = 2t ． 答：每月通话时间 240 分钟，按 A、B 两类收费标准缴费，所缴话费相等． 第 11 页，共 11 页 15. 解： 1 甲 = 2 千米 小时，V 乙 = t 千米 小时 2 设甲船的解析式为 = ， 过点 Ͳ1 ， 1 = ， 即 = 2 ， = 2 ， 设乙船的解析式为 = ܽ +   ， 过点 2Ͳ ， Ͳ1 = 2ܽ +   1 = ܽ +   ܽ = t   = = t 2 ； 3 根据题意，得 = 2 = t 解之，得 = t = ， 所以当 = t ，即乙船出发 t 2 = 2 小时赶上甲船． 16. 解： 11Ͳ25 2 由图像可知：小华在报亭看报时间 = 2 1 = 1 分钟 3 由图像得：小华看完报后到体育馆所用的时间 = 25 2 = 5 分钟， 小华看完报后到体育馆的路程 = 1 5 = 5 米， 则小华看完报后到体育馆的平均速度 = 5 5 = 1 米 分钟．