2021中考数学复习微专题 探索三角形相似的条件典型习题汇编）（无答案） 5页

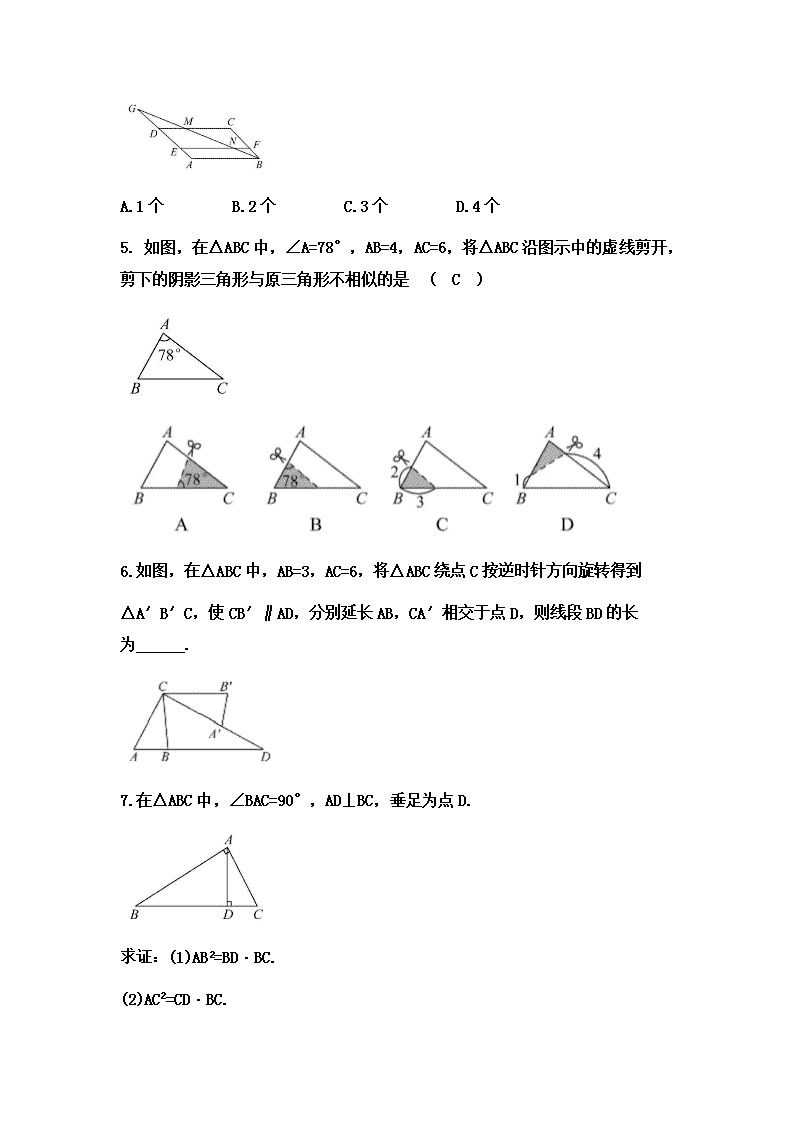
中考数学复习微专题 （探索三角形相似的条件典型习题汇编） 知识点一：利用两角相等判定三角形相似 1.如图，点 F 在平行四边形 ABCD 的边 AB 上，射线 CF 交 DA 的延长线于点 E，在 不添加辅助线的情况下，与△AEF 相似的三角形有( ) A.0 个 B.1 个 C.2 个 D.3 个 2.如图，在△ABC 中，DE∥BC， 〠 = ，BC=12，则 DE 的长是( ) A.3 B.4 C.5 D.6 3.已知一个三角形的两个内角分别是 40°，60°，另一个三角形的两个内角分 别是 40°，80°，则这两个三角形 ( ) A.一定不相似 B.不一定相似 C.一定相似 D.不能确定 4.如图，在▱ABCD 中，点 E，F 分别在边 AD，BC 上，且 EF∥CD，G 为边 AD 延长 线上一点，连接 BG，则图中与△ABG 相似的三角形有 ( ) A.1 个 B.2 个 C.3 个 D.4 个 5. 如图，在△ABC 中，∠A=78°，AB=4，AC=6，将△ABC 沿图示中的虚线剪开， 剪下的阴影三角形与原三角形不相似的是 ( C ) 6.如图，在△ABC 中，AB=3，AC=6，将△ABC 绕点 C 按逆时针方向旋转得到 △A′B′C，使 CB′∥AD，分别延长 AB，CA′相交于点 D，则线段 BD 的长 为 . 7.在△ABC 中，∠BAC=90°，AD⊥BC，垂足为点 D. 求证：(1)AB2=BD·BC. (2)AC2=CD·BC. 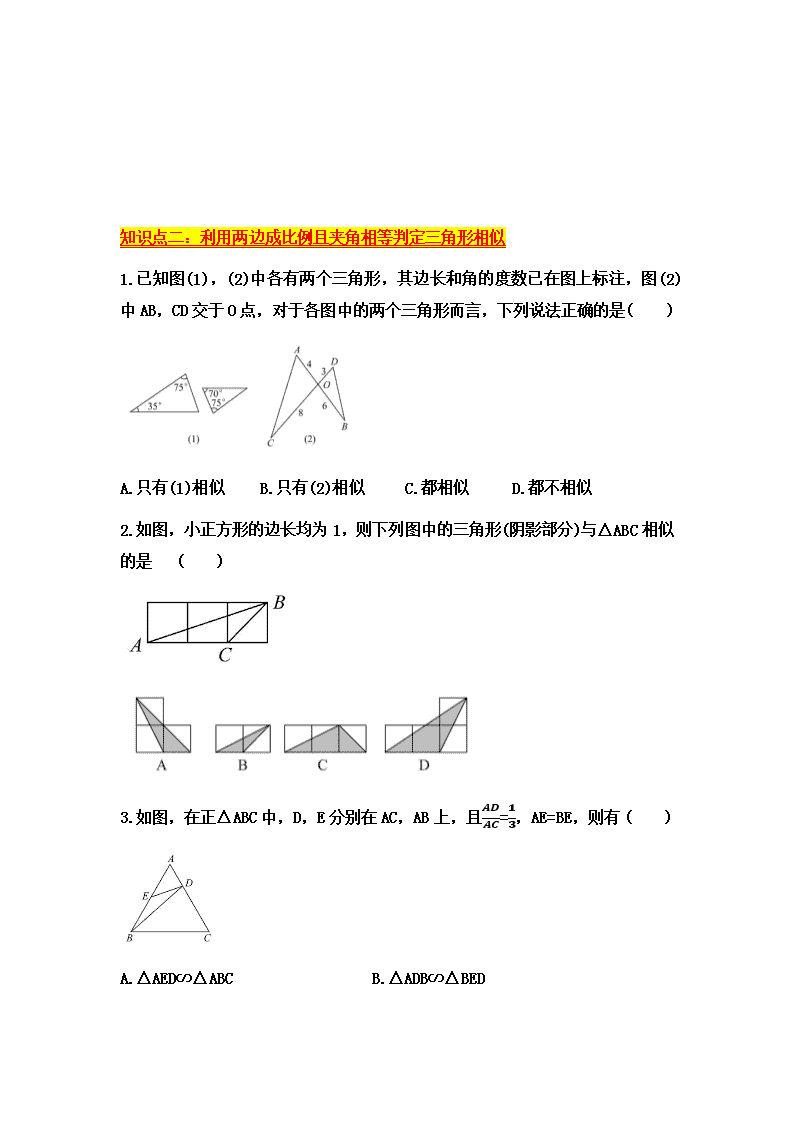知识点二：利用两边成比例且夹角相等判定三角形相似 1.已知图(1)，(2)中各有两个三角形，其边长和角的度数已在图上标注，图(2) 中 AB，CD 交于 O 点，对于各图中的两个三角形而言，下列说法正确的是( ) A.只有(1)相似 B.只有(2)相似 C.都相似 D.都不相似 2.如图，小正方形的边长均为 1，则下列图中的三角形(阴影部分)与△ABC 相似 的是 ( ) 3.如图，在正△ABC 中，D，E 分别在 AC，AB 上，且 〠 = ，AE=BE，则有 ( ) A.△AED∽△ABC B.△ADB∽△BED C.△BCD∽△ABC D.△AED∽△CBD 4.如图，AB，CD 交于点 O，且 OC=45，OD=30，OB=36，当 OA= 时，△AOC∽ △BOD. 5. 在△ABC 中，AB=9，AC=6，点 E 在 AB 上，且 AE=3，点 F 在 AC 上，连接 EF， 若△AEF 与△ABC 相似，则 AF=_____. 6.在△ABC 中，AB=6，AC=8，D，E 分别在 AB，AC 上，连接 DE，设 BD=x(0