2021中考数学复习微专题 反比例函数易错考点解析与练习提升 6页

中考数学微专题：反比例函数易错考点解析与练习提升 考点一：忽视隐含条件“k≠0”出错 例 1.当 m =————————时，函数 2 my (m 3)x   是反比例函数 错解：∵此函数是反比例函数 所以 2－ m =－1，解得 3m ， 当 3m 时，此函数是反比例函数. 错解分析：要特别注意把反比例函数 k xy  （k≠0）的形式写出类似整式形式 1y kx ， 这是因为 k≠0 有这个必备条件，而错解忽视了这个隐含条件. 正解：由题意，得      03 12 m m , 解得      3 3 m m ,因此 m =3， 即当 m=3 时此函数是反比例函数. 考点二：忽视实际问题中自变量的取值范围出错 例 2.三角形的面积为 8 2cm ，这时底边上的高 y(cm )与底边 x（cm ）之间的函数关系的图 象大致是（ ） 错解：选 B.由三角形的面积公式，得 82 1 xy ,  16 xy  故选 B. 错解分析：错解忽视了实际问题中自变量的取值范围（x>0 这一条件） 正解： 选 D.由三角形的面积公式，得 1 2 xy 8  16 xy  （x>0），故选 D. 考点三：忽视比例系数的不同出错 例 3.已知 y 与 2x 成正比例， 2x 与 1 z 成反比例，求 y 与 z 的函数关系式 错解： y 与 2x 成正比例，  2y kx ， 又 2x 与 z 1 成反比例，  1 z 2 kx  ， 即 )0(2  kkzx ， zkkzkkxy 22  . 错解分析： 2y kx 和 1 z 2 kx  是两个不同函数关系式，它们的比例系数是不同的，不能将两 个关系式的比例系数都用 k 表示，要区分开来. 正解： y 与 2x 成正比例， 2x 与 1 z 成反比例  2 1y k x ， 2 2x k z （ 1 2k ,k 均不等于 0）， zkky 21 （ 021 kk ）. 考点四：忽视反比例函数的性质成立的条件出错 例 4.在函数 2m 1 xy   （m 为常数）的图象上有三点(-3, 1y ),(-1 , 2y ) ,(3 , 3y ) 则函 数值的大小关系是（ ） A. 321 yyy  B. 123 yyy  C. 132 yyy  D. 213 yyy  错解： 0)1(1 22  mm ，  y 随 x 的增大而增大，于是有 321 yyy  ，故应选 A. 错解分析：讨论反比例函数 y 随 x 的变化关系时，一定要根据图象所在的象限讨论，不能一 概而论. 正解： 2 2m 1 (m 1) 0      ， 图 象 分 布 在 第 二 、 四 象 限 内 ， 且 在 各 象 限 内 ， y 随 x 的 增 大 而 增 大 ， 由 题 知 点 (-3, 1y ),(-1 , 2y ) 在第二象限分支上，又因为 -3<-1,所以 210 yy  ，而 点(3 , 3y )在第四象限的分支上，所以 3y <0，因此有 213 yyy  ，故应选 D. 说明:本题宜采用数形结合法求解，即画出函数 x my 12  的图象，然后大致描出这三点，即 可判断其大小关系. 考点五：忽视分类讨论出错 例 5．已知反比例函数 k xy (k 0)  的图象上有两点 A（ 11 , yx ）,B（ 22 , yx ），且 21 xx  ， 则 21 yy  的值是（ ） A 正数 B 负数 C 非负数 D 不能确定 错解：因为 k<0 所以反比例函数 k xy (k 0)  的图象分布在第二、四象限，又 21 xx  ， 由反比例函数的性质知 1 2y y ，所以 21 yy  <0 , 即 21 yy  是负数，选 B. 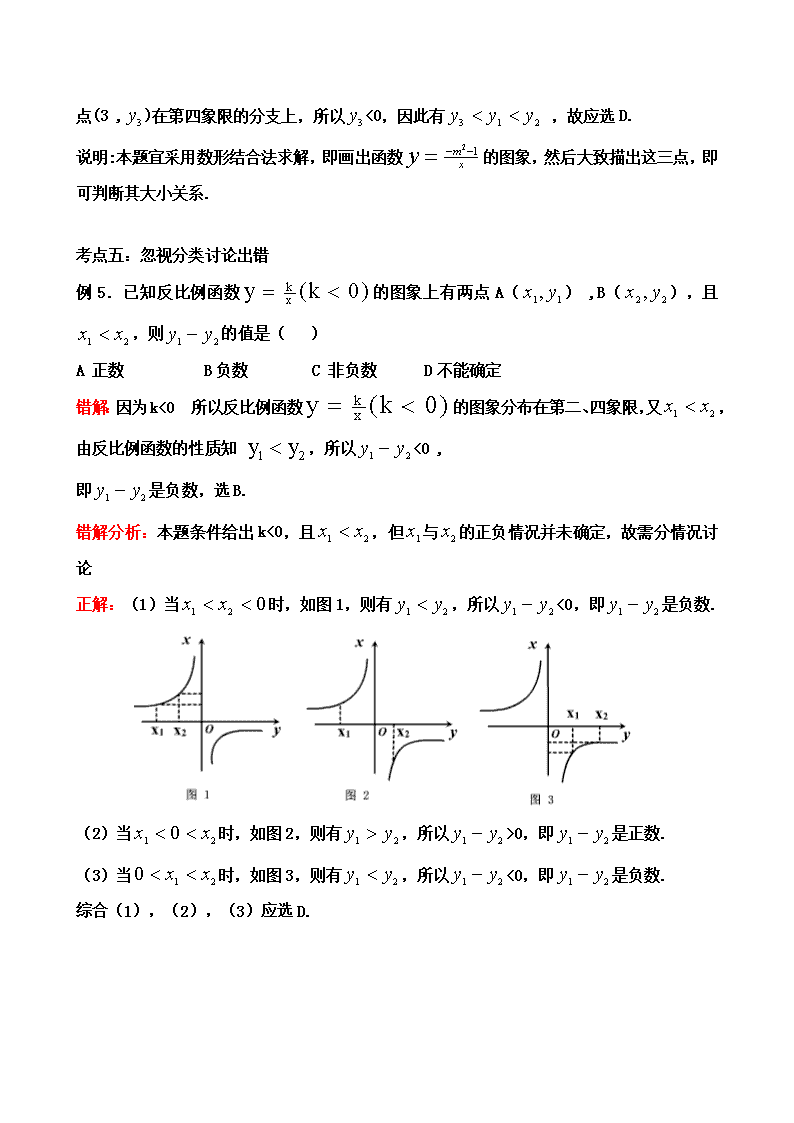错解分析：本题条件给出 k<0，且 21 xx  ，但 1x 与 2x 的正负情况并未确定，故需分情况讨 论 正解：（1）当 021  xx 时，如图 1，则有 21 yy  ，所以 21 yy  <0，即 21 yy  是负数. （2）当 21 0 xx  时，如图 2，则有 21 yy  ，所以 21 yy  >0，即 21 yy  是正数. （3）当 210 xx  时，如图 3，则有 21 yy  ，所以 21 yy  <0，即 21 yy  是负数. 综合（1），（2），（3）应选 D. 练习反馈 ： 1. 甲、乙两地相距 100 km，一辆汽车从甲地驶往乙地，汽车的平均速度是 x km/h，汽车从 甲地到乙地所用的时间是 yh.下列图象中能大致表示 y 与 x 关系的是（ ） （A） （B） （C） （D） 2. 函数 y= 的图象可能是 ( ) 3. 点(2,-4)在反比例函数 y= 的图象上,则下列各点在此函数图象上的是 ( ) A.(2,4) B.(-1,-8) C.(-2,-4) D.(4,-2) 4. 已知反比例函数 y= (k>0)的图象经过点 A(1,a),B(3,b),则 a 与 b 的关系正确的是 ( ) A.a=b B.a=-b C.ab 5. 如图,市煤气公司计划在地下修建一个容积为 104m3 的圆柱形煤气储存室,则储存室的底面 积 S(单位:m2)与其深度 d(单位:m)的函数图象大致是 ( ) 6. 若 y=(m2-3m)x|m|-4 为反比例函数,则 m= . 7. 已知反比例函数 y= (k≠0)的图象如图所示,则 k 的值可能是 . (写一个即可). 8. 已知反比例函数 y= (k≠0)的图象经过点(3,-1),则当 1y2 时 x 的取值范围. 12. 如图,在直角坐标系中,直线 y=- x 与反比例函数 y= 的图象交于关于原点对称的 A,B 两 点,已知点 A 的纵坐标是 3. (1)求反比例函数的表达式. (2)将直线 y=- x 向上平移后与反比例函数在第二象限内交于点 C,如果△ABC 的面积为 48,求 平移后的直线的函数表达式.