初二下学期期中数学练习 3 10页

一、选择题（每小题的四个选项中，只有一个是符合题目要求的．请将你认为符合要求的一项的序号 填在题中的括号内．每小题 3 分，共 30 分） 1．下列函数中，一次函数是（ ）． A． 2y x  B． y x C． 22y x D． 3 1y x  【答案】D 【解析】 A 、反比例函数， C 、二次函数， D 、一次函数． 故选 D ． 2．下列每一组数据中的三个数值分别为三角形的三边长，不能构成直角三角形的是（ ）． A． 3， 4 ，5 B． 6 ，8，10 C． 3 ， 2 ， 5 D．1，1， 2 【答案】C 【解析】根据勾股逆定理，可判断 A 、 B 、 D 都成立． 故选 C ． 4．下列给出的条件中，不能判定四边形 ABCD 是平行四边形的是（ ）． A． AB CD ， AD BC B． AD BC ， AD BC‖ C． AB CD ， B D   D． AB CD‖ ， A C   【答案】C 【解析】两组对边分别平行的四边形是平行四边形，故 A 正确， 一组对边平行且相等的四边形是平行四边形，故 B 正确， 连接 BD ，利用全等三角形 AAS，即可证明，故 D 正确， 故选 C ． 8．如图，直线 y kx b  与 x 轴交于点 ( 4,0) ，当 0y  时， x 的取值范围是（ ）． A． 4x   B． 0x  C． 4x   D． 0x  【答案】A 【解析】根据图象可看出，当 0y  时， 4x   ， 故选 A ． 二、填空题（请将正确答案填在题中的横线上．每小题 3 分，共 24 分） 12．函数 2 1 xy x   自变量 x 的取值范围是__________． 【答案】 1 2x  【解析】二次根式 2 1x  ，当 2 1 0x  ≥ 时，即 1 2x≥ 时，二次根式有意义， 又因为 2 1x  位于分母，所以当 1 2x  时，函数有意义． 16．下列 3 3 网格图都是由 9 个相同的小正方形组成，每个网格图中有 3个小正方形已涂上阴影，请在 余下的 6 个空白小正方形中，按下列要求涂上阴影： （1）选取1个涂上阴影，使 4 个阴影小正方形组成一个轴对称图形，但不是中心对称图形． （ 2 ）选取1个涂上阴影，使 4 个阴影小正方形组成一个中心对称图形，但不是轴对称图形． （ 3）选取 2 个涂上阴影，使5 个阴影小正方形组成一个轴对称图形． （请将三个小题依次作答在图 1、图 2、图 3 中，均只需画出符合条件的一种情形） 【答案】见解析 【解析】 （1） （ 2 ） （ 3） 18．在平面直角坐标系中，直线 : 1l y x  与 x 轴交于点 1A ，如图所示依次作正方形 1 1 1A B C O 、正方形 2 2 2 1A B C C 、 、正方形 1n n n nA B C C  ，使得点 1A 、 2A 、 3A 、 在直线 l 上，点 1C 、 2C 、 3C 、 在 y 轴 正半轴上，则点 3B 的坐标是__________，点 nB 的坐标是__________． 【答案】 (4,7) , 1(2 ,2 1)n n  【解析】令 1 0x   ， ∴ 1x  ， 将 1x  代入 y x ， 0y  ， ∴ 1(1,0)A ， ∵四边形 1 1 1A B C O 为正方形， ∴ 1(1,1)B ， ∵ 1 2C A x‖ 轴， ∴ 2 (2,1)A ， ∵四边形 2 2 2 1A B C C 是正方形， ∴ 2 (2,3)B ， 同理可得 3 (4,3)A ， 3 (4,7)B ， ∴ 1(2 ,2 1)n n nB   ． 三、解答下列各题（共 46 分） 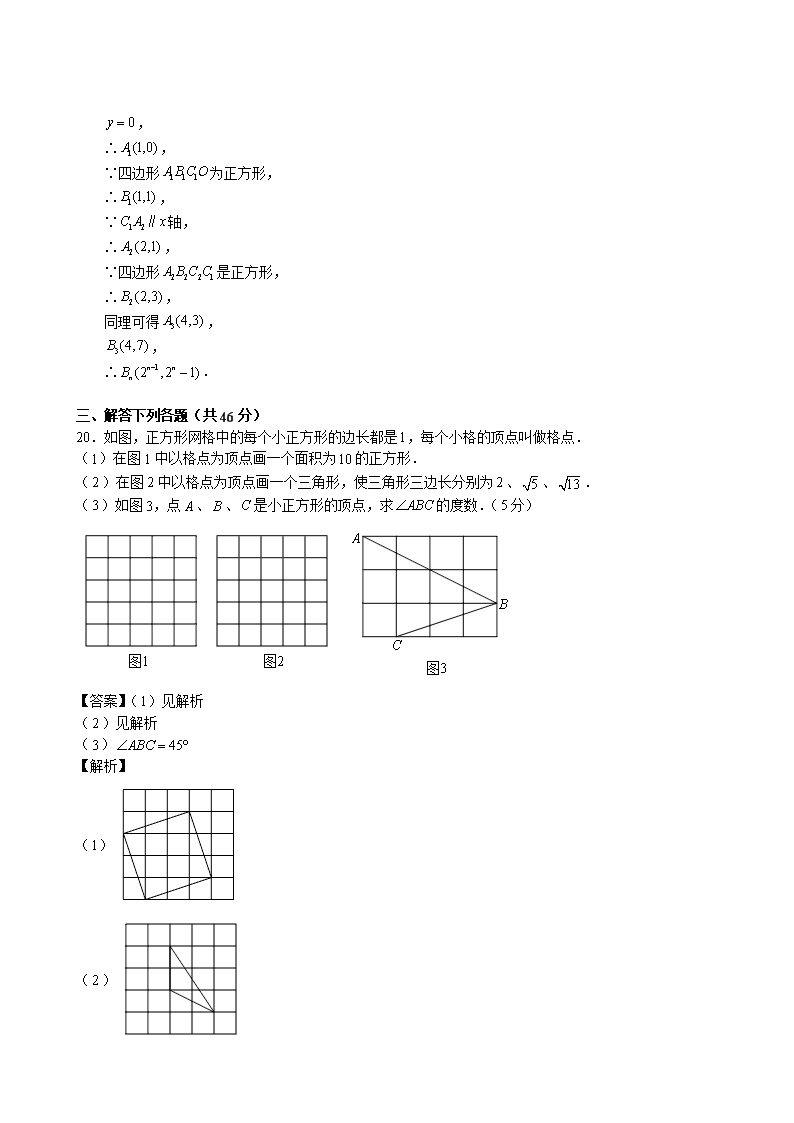20．如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点． （1）在图 1 中以格点为顶点画一个面积为10 的正方形． （ 2 ）在图 2 中以格点为顶点画一个三角形，使三角形三边长分别为 2 、 5 、 13 ． （ 3）如图 3，点 A 、 B 、 C 是小正方形的顶点，求 ABC 的度数．（ 5 分） 【答案】（1）见解析 （ 2 ）见解析 （ 3） 45ABC   【解析】 （1） （ 2 ） （ 3） 连接 AC ， CD ， 则 2 22 1 5AD BD CD     ， 由勾股定理： 2 23 1 10AC BC    ， ∴ 45ABC BAC     ． 21．如图，已知平行四边形 ABCD 中， BF FD ，求证：四边形 AECF 是平行四边形．（ 6 分） 【答案】见解析 【解析】∵四边形 ABCD 是平行四边形， ∴ AD BC‖ ，且 AD BC ， ∴ AF EC‖ ， ∵ BE DF ， ∴ AF EC ， ∴四边形 AECF 是平行四边形． 23．已知一次函数的图象过点 (3,5) 与 ( 4, 9)  ，求这个一次函数的解析式，并求出直线与坐标轴围成的 三角形面积．（5 分） 【答案】 1 4 【解析】设函数解析式 y kx b  ， 将 (3,5) 与 ( 4, 9)  代入， 得 5 3 9 4 k b k b       ， 解得 2 1 k b     ， ∴函数解析式： 2 1y x  ． 令 0y  ， 得 2 1 0x   ， 1 2x  ， 令 0x  ， 得 1y   ， ∴函数与 x 轴交于 1 ,02      ， 与 y 轴交于 (0, 1) ． ∴ 1 1 112 2 4S      ． 24．如图，在平面直角坐标系 xOy 中，一次函数 y kx b  的图象与 x 轴交于点 ( 3,0)A  ，与 y 轴交于点 B ，且与正比例函数 4 3y x 的图象的交点为 ( ,4)C m ． （1）求一次函数 y kx b  的解析式． （ 2 ）求 BOC△ 的面积．（ 6 分） 【答案】（1） 2 23y x  （ 2 ） 3 【解析】（1）∵ C 在正比例函数图像上， ∴ 4 43 m  ， ∴ 3m  ， ∵点 (3,4)C 、 ( 3,0)A  在一次函数上， ∴代入可得， 3 0 3 4 k b k b       ， 解得 2 3 2 k b     ， ∴ 2 23y x  ， （ 2 ）令 0x  ， 得 2y  ， ∴ (0,2)B ， ∴ 2OB  ， 作 CD y⊥ 轴于 D ， 3CD  ， ∴ 1 2BOCS BO CD  △ 1 2 32    3 ． 25．直线 2 43y x  与 x 轴、 y 轴分别交于点 A 和点 B ，点 C 、 D 分别为线段 AB 、 OB 的中点，点 P 为 OA上一动点，请你在所给的坐标系中准确的画出点 P 的位置并求出 PC PD 值最小时点 P 的坐标．（ 6 分） 【答案】 3,02P    【解析】令 2 43y x  中， 0x  ，则 4y  ， ∴ (0,4)B ， 令 0y  ，则 6x   ， ∴ ( 6,0)A  ， ∵ C 、 D 分别为线段 AB 、 OB 的中点， ∴ ( 3,2)C  ， (0,2)D ， 作 D 关于 x 轴对称点 D ， ∴ (0, 2)D  ， 设直线 CD 解析式 y kx b  ， ∴ 2 3 2 k b b      ， ∴ 4 3 2 k b       ， ∴ 4 23y x   ． 令 0y  ，则 3 2x   ， ∴ 3,02P    ． 26．探究问题： （1）方法感悟： 如图①，在正方形 ABCD 中，点 E ， F 分别为 DC ， BC 边上的点，且满足 45EAF   ，连结 EF ， 求证： DE BF EF  ． 感悟解题方法，并完成下列填空： 将 ADE△ 绕点 A 顺时针旋转 90 得到 ABG△ ，此时 AB 与 AD 重合，由旋转可得： AB AD ， BG DE ， 1 2   ， 90ABG D     ， ∴ 90 90 180ABG ABF        ， 因此，点 G ， B ， F 在同一条直线上． ∵ 45EAF   ，∴ 2 3 90 45 45BAD EAF            ． ∵ 1 2   ，∴ 1 3 45     ． 即 GAF  __________． 又 AG AE ， AF AF ， ∴ GAF△ ≌__________． ∴__________ EF ，故 DE BF EF  ． （ 2 ）方法迁移： 如图②，将 Rt ABC△ 沿斜边翻折得到 ADC△ ，点 E ，F 分别为 DC ，BC 边上的点，且 1 2EAF DAB   ， 试猜想 DE ， BF ， EF 之间有何数量关系，并证明你的猜想． （ 3）问题拓展： 如图③，在四边形 ABCD 中， AB AD ， E ， F 分别为 DC ， BC 上的点，满足 1 2EAF DAB   ， 试猜想当 B 与 D 满足什么关系时，可使得 DE BF EF  ，请直接写出你的猜想（不必说明理由）．（8 分） 【答案】（1） EAF ， EAF△ ，GF （ 2 ）见解析 （ 3）见解析 【解析】（1） EAF ， EAF△ ，GF （ 2 ） EF DE BF  ， 证明：延长 CF ，作 4 1   ， ∵将 Rt ABC△ 沿斜边翻折得到 ADC△ ， 点 E 、 F 分别为 DC 、 BC 边上的点， 且 1 2EAF DAB   ， ∴ 1 2 3 5       ， 2 3 1 5       ， ∵ 4 1   ， ∴ 2 3 4 5       ， ∴ GAF FAE   ， 在 AGB△ 和 AED△ 中， 4 1 AB AD ABG ADE         ， ∴ AGB△ ≌ (ASA)AED△ ， ∴ AG AE ， BG DE ， 在 AGF△ 和 AEF△ 中， AG AE GAF EAF AF AF       ， ∴ AGF△ ≌ (SAS)AEF△ ， ∴ GF EF ， ∴ DE BF EF  ． （ 3）当 180B D     时，可使得 DE BF EF  ， 延长 CF ，作 2 1   ， ∵ 180ABC D    ， 180ABC ABG    ， ∴ D ABG   在 AGB△ 和 AED△ 中， 2 1 AB AD D ABG         ， ∴ AGB△ ≌ (ASA)AED△ ， ∴ BG DE ， AG AE ， ∵ 1 2EAF DAB   ， ∴ EAF GAF   ， 在 AGF△ 和 AEF△ 中， AG AE GAF EAF AF AF       ， ∴ AGF△ ≌ (SAS)AEF△ ， ∴ GF EF ， DE BF EF  ．