九年级数学上册第六章反比例函数小结与复习课件新版北师大版 28页

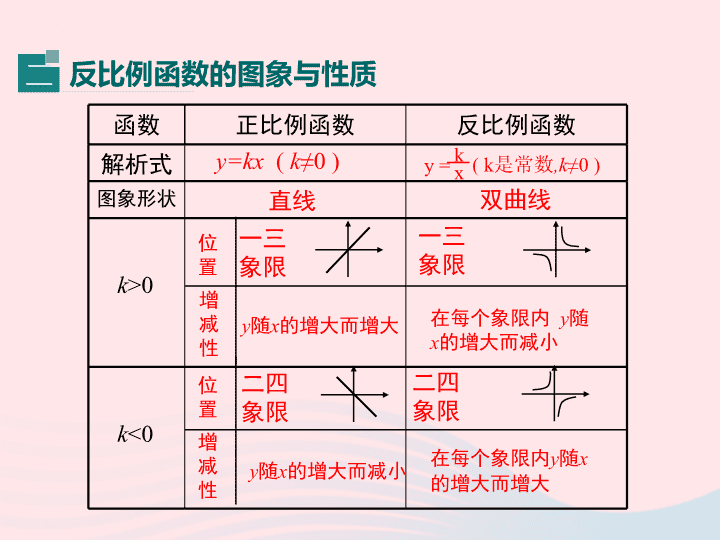
小结 与 复习 第六章 反比例函数 导入新课 讲授新课 当堂练习 课堂小结 反比例函数的定义 一 1. 反比例函数的定义 : 函数 y = ( k 是常数 , 且 k ≠0 ) 叫做反比例函数 . 2. 反比例函数解析式的变形式 : (1) y = kx -1 ( k ≠0) (2) xy=k ( k ≠0) 要点梳理 反比例函数的图象与性质 二 函数 正比例函数 反比例函数 解析式 图象形状 k >0 k <0 位置 增减性 位置 增减性 y=kx ( k ≠0 ) x k ( k 是常数 ,k ≠0 ) y = 直线 双曲线 一三象限 y 随 x 的增大而增大 一三象限 在每个象限内 y 随 x 的增大而减小 二四象限 二四象限 y 随 x 的增大而减小 在每个象限内 y 随 x 的增大而增大 1 . 反比例函数的图象是两支曲线， 2.当 k >0 时，图象分别位于第一、三象限；当 k <0 时，图象分别位于第二、四象限 . 3 . 当 k >0 时 . 在每一个象限内， y 随 x 的增大而减小；当 k <0 时，在每一个象限， y 随 x 的增大而增大 . 4 . 因为在 y= k/x ( k ≠0) 中， x 不能为 0 ， y 也不能为 0 ，所以反比例函数的图象不可能与 x 轴相交，也不可能与 y 轴相交 . 5 . 在一个反比例函数图象上任取两点 P 、 Q ，过点 P 、 Q 分别作 x 轴， y 轴的平行线，与坐标轴围成的矩形面积为 S 1 、 S 2 ， 则 S 1 ＝ S 2 反比例函数图象解读 k 的几何意义：反比例函数图像上的点 ( x ， y ) 具有两坐标之积 ( xy ＝ k ) 为常数这一特点，即过双曲线上任意一点，向两坐标轴作垂线， 两条垂线与坐标轴所围成的矩形的面积为常数 | k | . 规律：过双曲线上任意一点，向两坐标轴作垂线， 一条垂线与坐标轴、原点所围成的三角形的面积为常数 ． 反比例函数 比例系数k的几何意义 三 反比例函数的应用 四 一般解题步骤 应用类型 与数学问题相结合 学科间的综合（物理公式） 审题、准确判断数量关系 建立反比例函数的模型 根据实际情况确定自变量的取值范围 实际问题求解 考点讲练 【解析】把P(1，－3)代入 (k≠0)得k＝1×(－3)＝－3.故选B. 　 B 考点一 反比例函数的图象与性质 D 　 【解析】方法一：分别把各点代入反比例函数求出 y 1 ， y 2 ， y 3 的值，再比较出其大小即可． 方法二：根据反比例函数的图象和性质比较． 比较反比例函数值的大小，在同一个象限内根据反比例函数的性质比较，在不同象限内，不能按其性质比较，函数值的大小只能根据特征确定． 归纳 针对训练 1. 已知函数 ， y 随 x 的增大而减小，求 a 的值和表达式（只考虑学过的函数） . 解：当函数为正比例函数时， a 2 + a -5=1 ，解得 a 1 =-3, a 2 =2. ∵ y 随 x 的增大而减小 ,∴ a =-3. 当函数为反比例函数时， a 2 +a -5=-1 ，解得 ∵ y 随 x 的增大而减小， 2 . 函数 ( k 为常数）的图象上有三点 （－ 3, y 1 ） , （－ 1, y 2 ） , （ 2, y 3 ） , 则函数值 y 1 、 y 2 、 y 3 的大小关系是 _______________; y 3 < y 1 < y 2 1 考点二 与反比例函数 k 有关的问题 利用反比例函数中 k 的几何意义时，要注意点的坐标与线段长之间的转化，并且利用关系式和横坐标，求各点的纵坐标是求面积的关键． 归纳 针对训练 3. 如图：M为反比例函数y＝ 图象上一点，MA⊥y轴于A，S △MAO =2时，k= ． 4 4. 如图，点 A 在双曲线 y ＝ 上，点 B 在双曲 线 y ＝ 上，且 AB ∥ x 轴， C ， D 在 x 轴上，若四边形 ABCD 为矩形，则它的面积为 ________ ． 2 y x O A 考点三 反比例函数与一次函数的综合 解：(1)将点 A ( m ，2)的坐标代入一次函数 y 1 ＝ x ＋1 得2＝m＋1，解得m＝1. 即点A的坐标为(1，2)． 将点A(1，2)的坐标代入反比例函数 得k＝2. ∴反比例函数的解析式为 (2)当0＜x＜1时，y 1 ＜y 2 ； 当x＝1时， y 1 ＝ y 2 ； 当x＞1时， y 1 ＞ y 2 . y x O A 此类一次函数，反比例函数，二元一次方程组，三角形面积等知识的综合运用，其关键是理清解题思路，在直角坐标系中，求三角形或四边形面积时，常常采用分割法，把所求的图形分成几个三角形或四边形，分别求出面积后再相加． 归纳 5. 如图，一次函数 y=kx -1 的图象与反比例函数 y= 的图象交于 A ， B 两点，其中点 A 的坐标为 （ 2 ， 1 ） . （ 1 ）试确定 k ， m 的值； （ 2 ）求点 B 的坐标 . y x O 1 2 A B 针对训练 （1）将 （2，1） 代入 y= ，得 m =1×2=2 . 将 （2，1） 代入 y=kx -1 ，得 k =1 . ∴两个函数的表达式为 y = ， y=x -1. （2）将 y = 和 y = x -1 组成方程组为 y = ， y=x -1 . 解得 x 1 =-1， y 1 =-2， x 2 =2， y 2 =1. ∴点 B 的坐标为 （-1，-2） . y x O 1 2 A B 例 5 病人按规定的剂量服用某种药物，测得服药后 2 小时， 每毫升血液中的含药量达到最大值为 4 毫克．已知服药 后， 2 小时前每毫升血液中的含药量 y ( 单位：毫克 ) 与时间 x ( 单 位：小时 ) 成正比例； 2 小时后 y 与 x 成反比例 ( 如图 ) ．根 据以上信息解答下列问题： (1) 求当 0≤ x ≤2 时， y 与 x 的函数解析式； (2) 求当 x >2 时， y 与 x 的函数解析式； (3) 若每毫升血液中的含药量不低于 2 毫克时治疗有效，则 服药一次，治疗疾病的有效时间是多长？ 考点四 反比例函数的应用 解： (1) 当 0≤ x ≤2 时， y 与 x 成正比例函数关系． 设 y ＝ kx ，由于点 (2,4) 在直线上， 所以 4 ＝ 2 k ， k ＝ 2 ，即 y ＝ 2 x . (2)当x>2时，y与x成反比例函数关系，设 由于点(2,4)在图象上， 所以 ，即k＝8. 即 (3) 当 0≤ x ≤2 时，含药量不低于 2 毫克，即 2 x ≥2 ， x ≥1. 即服药 1 小时后；当 x >2 时，含药量不低于 2 毫克， 所以服药一次，治疗疾病的有效时间是 1 ＋ 2 ＝ 3( 小时 ) ． 注意:不要忽略自变量的取值范围． 用一次函数与反比例函数解决实际问题，先理解清楚题意，把文字语言转化为数学语言， 列出相应的不等式（方程），若是方案选择问题，则要求出自变量在取不同值时所对应的函数值，判断其大小关系，结合实际需求，选择最佳方案 . 方法总结 6. 某天然气公司要在地下修建一个容积为 10 5 m 3 的圆柱形天然气储存室 . （ 1 ）储存室的底面积 S （ m 2 ） 与其深度 d （ m ） 有怎样的函数关系？ （ 2 ）若公司决定把储存室的底面积 S 定为 5000m 2 , 则施工队施工时应该向下掘进多深？ （ 3 ）当施工队按（ 2 ）中的计划掘进到地下 15m 时，碰上了坚硬的岩石，为了节约建设资金，公司决定把储存室的深度改为 15m ，则相应地储存室的底面积应改为多少才能满足需要？（精确到 0.01m 2 ） 针对训练 储存室的底面积 S （ m 2 ） 与其深度 d （ m ） 有怎样的函数关系 ？ （ 1 ） 解 （ d ＞ 0 ） . （ 2 ）若公司决定把储存室的底面积 S 定为 5000m 2 ， 则施工队施工时应该向下掘进多深 ？ 解 中 时： （ m ） . 当施工队按（ 2 ）中的计划掘进到地下 15 m 时， 碰上了坚硬的岩石，为了节约建设资金，公司 决定把储存室的深度改为 15 m ，则相应地储存 室的底面积应改为多少才能满足需要 （ 精确到 0.01 ） ？ （ 3 ） 时： 中 解 中 解 实际问题 建立反比例函数模型 反比例函数的图象与性质 反比例函数的应用 课堂小结