反比例函数的图象和性质 3页

年 级 九 年 级 课 题 26.1.2 反比例函数的图象和性质 课 型 新 授 教 学 媒 体 多 媒 体 会用描点法画反比例函数的图象 结合图象分析并掌握反比例函数的性质 教 学 目标 体会函数的三种表示方法，领会数形结合的思想方法 理解并掌握反比例函数的图象和性质重点 难点 理解并掌握反比例函数的图象和性质 教师准备教学 准备 学生准备 是否需要课 件 教学过程设计 课堂引入 提出问题： 1．一次函数 y＝kx＋b（k、b 是常数，k≠0）的图象是什么？其性质有哪些？正比例函数 y＝kx （k≠0）呢？ 2．画函数图象的方法是什么?其一般步骤有哪些？应注意什么？ 3．反比例函数的图象是什么样呢? 例习题分析 例 2．见教材 P48，用描点法画图，注意强调： （1）列表取值时，x≠0，因为 x＝0 函数无意义，为了使描出的点具有代表性，可以“0”为 中心，向两边对称式取值，即正、负数各一半，且互为相反数，这样也便于求 y 值 （2）由于函数图象的特征还不清楚，所以要尽量多取一些数值，多描一些点，这样便于连线， 使画出的图象更精确 （3）连线时要用平滑的曲线按照自变量从小到大的顺序连接，切忌画成折线 （4）由于 x≠0，k≠0，所以 y≠0，函数图象永远不会与 x 轴、y 轴相交，只是无限靠近两坐 标轴 例 1．（补充）已知反比例函数 的图象在第二、四象限，求 m 值，并指出在 每个象限内 y 随 x 的变化情况？ 分析：此题要考虑两个方面，一是反比例函数的定义，即 （k≠0）自变量 x 的指数是 －1，二是根据反比例函数的性质：当图象位于第二、四象限时，k＜0，则 m－1＜0，不要忽视这个条 件 略解：∵ 是反比例函数 ∴m2－3＝－1，且 m－1≠0 又∵图象在第二、四象限 ∴m－1＜0 解得 且 m＜1 则 留白： （ 供 教 师 个 性 化设计） 32 )1( −−= mxmy 1−= kxy 32 )1( −−= mxmy 2±=m 2−=m 例 2．（补充）如图，过反比例函数 （x＞0）的图象上任意 两点 A、B 分别作 x 轴的垂线，垂足分别为 C、D，连接 OA、OB，设△ AOC 和△BOD 的面积分别是 S1、S2，比较它们的大小，可得（ ） （A）S1＞S2 （B）S1＝S2 （C）S1＜S2 （D）大小关系不能确定 分析：从反比例函数 （k≠0）的图象上任一点 P（x，y）向 x 轴、y 轴作垂线段，与 x 轴、y 轴所围成的矩形面积 ，由此可得 S1＝S2 ＝ ，故选 B 随堂练习 1．已知反比例函数 ，分别根据下列条件求出字母 k 的取值范围 （1）函数图象位于第一、三象限 （2）在第二象限内，y 随 x 的增大而增大 2．函数 y＝－ax＋a 与 （a≠0）在同一坐标系中的图象可能是（ ） 3．在平面直角坐标系内，过反比例函数 （k＞0）的图象上的一点分别作 x 轴、y 轴的垂 线段，与 x 轴、y 轴所围成的矩形面积是 6，则函数解析式为 xy 1= x ky = kxyS == 2 1 x ky −= 3 x ay −= x ky = 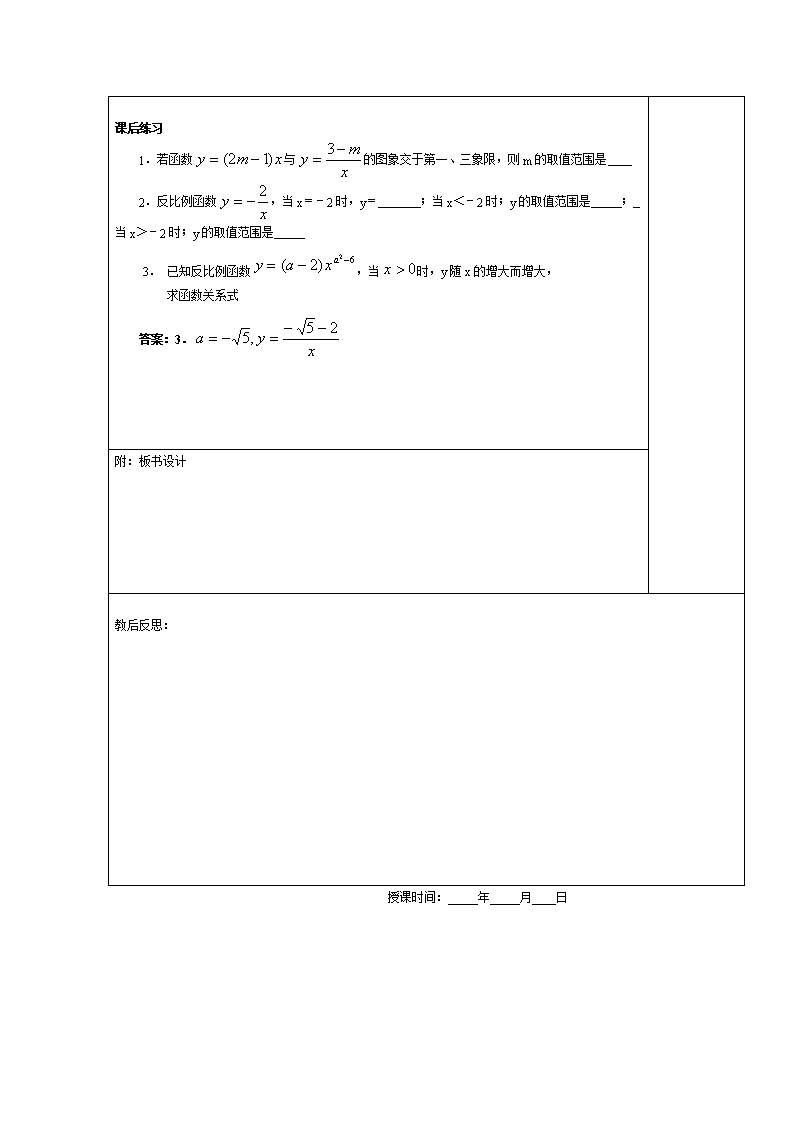课后练习 1．若函数 与 的图象交于第一、三象限，则 m 的取值范围是 2．反比例函数 ，当 x＝－2 时，y＝ ；当 x＜－2 时；y 的取值范围是 ； 当 x＞－2 时；y 的取值范围是 3． 已知反比例函数 ，当 时，y 随 x 的增大而增大， 求函数关系式 答案：3． 附：板书设计 教后反思： 授课时间：_____年_____月____日 xmy )12( −= x my −= 3 xy 2−= y a x a= − −( )2 2 6 x > 0 xya 25,5 −−=−=