（浙教版）九年级数学下册 同步备课系列专题3 29页

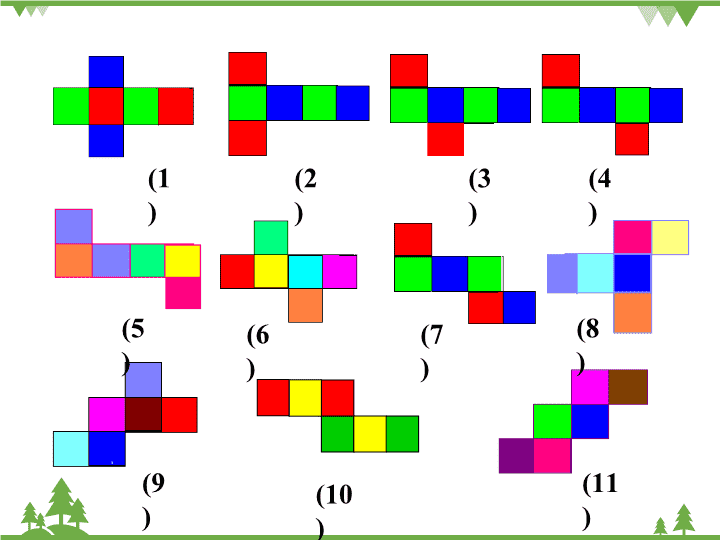
3.4 简单几何体的表面展开图 （第1课时） 浙教版九年级下册 将几何体沿某些棱剪开后铺平，且六个面连 在一起，这样的图形叫几何体的表面展开图. 请将一个立方体纸盒沿某些棱剪开，使 六个面连在一起，展成一个平面图形. 你能得到怎样的平面图形？ (1) (11)(10)(9) (8)(6)(5) (7) (2) (4)(3) 这是一个对面颜色相同的立方体 问题：立方体的相对两个面在其表面展开图 中有何位置关系？ 答：间隔一行或间隔一列 例1 图3-39是一个立方体的表面展开图吗？如果是，分 别用1，2，3，4，5，6中的同一个数字表示立方体和它 的展开图中各对对应的面（只要求给出一种表示法）. 解 图3-39是一个立方体的表面展开图，各对应面上 的数字表示如图3-40和图3-41. 分析 可以先用折叠的方法试一试，看它能否折成 一个立方体． 例2 如图3-42，为了生产这种牛奶 包装盒，需要先画出展开图纸样． （1）如图3-43给出三种纸样，它们 都正确吗？ （2）从图3-43正确的纸样中选出一 种，标注上尺寸． （3）利用你所选的一种纸样，求 出包装盒的侧面积和全面积（侧面 积与两个底面积的和）. 解 （1）图3-43中，因为表示底面的两个长方形不可 能在同一侧，所以图乙不正确．图甲和图丙都正确 （请动手试一试，为什么?). （2）根据图3-43，若选图甲，可得表而展开图 及尺寸标注如图3-44所示． （3）由图3-44得，包装盒的侧 面积和全面积为 S侧＝(b+a+b+a)h =2ah+2bh； S表＝S侧＋2S底 =2ah+2bh+2ab. 1、下面哪些图形经过折叠可以围成一个棱柱？ (1)(2)(4) 三 棱 柱 2、三棱柱的表面展开图 乙 丙甲 画出如图所示的底面为正三角 形的直棱柱的表面展开图. 36 10 某工厂要加工一批正六棱柱形状的食品盒，其三视图 如图，（单位：cm）问制作一个食品盒至少需要的硬 纸板的面积为多少？ 36 10 解：上下底面面 积 23 10 6 4    2300 3 cm ( ) 六个侧面面 积 36 10  22160 cm ( ) 6 2 所需硬纸板面积 为 300 3 2160 2cm( ) ( ) 答：所需面积 为…… 问题1：在生活中常遇的圆柱形物体，如：油桶、铅 笔、圆形柱子等．那么圆柱有哪些特征？ 油桶 铅笔、圆形柱子 圆形大厦 圆柱的性质 • ①圆柱的轴通过上、下底面的圆心，且垂 直于上、下底； • ②圆柱的母线平行于轴且长都相等，等于 圆柱的高； • ③ 圆柱的底面圆平行且相等． 　　问题1：将一张矩形的纸片围成圆柱的侧面积， 你发现有什么问题？ 能围成两个不同的圆柱 . 　　问题２:将课本的一边放在桌面上，然后以另外一 边所在直线为轴旋转一周，你发现了什么问题? 能旋转成两个不同的圆柱. 　　　圆柱体的形成 由矩形围成或者旋转而成. 问题3:将圆柱的侧面沿母线剪开，得到什么图形？ 你能想象出圆柱的展开图吗？ 例3 如图3-48为一个圆柱的三视图．以相同的 比例画出它的表面展开图，并计算它的侧面积 和全面积（结果保留π）. 分析 由图3-48知，圆柱底面圆的半径r为1cm， 母线长l为2.5cm.因此圆柱的表面展开图中两个 底面应画成半径为1cm的圆，侧面展开图应画 成长为2πr=2π×1≈6.28(cm)，宽为2.5cm的长方 形． 解 所求圆柱的表面展开图如图3-49. S侧=2πrl=2×π×1×2.5=5π（cm2)； S全=2πr2＋2πrl=2π×12+2π×1×2.5=7π（cm2). 答：这个圆柱的侧面积为5πcm2，全面积为7πcm2. 圆 锥 的 结 构 特 征 圆锥：以直角三角形的一条直角边所在的直线 为旋转轴，其余两边旋转形成的曲面所围成的 几何体叫做圆锥. 轴 A C B 母线 侧面 底面 圆锥用表示它的轴的字母表示. 展开 如图，将圆锥的侧面沿AB展开，得到一个什么 图形？圆锥的侧面展开图与△OAB又怎样的关系? 圆 锥 的 侧 面 展 开 图 r l l 2πr 180 n Rl   2 360 n RS   1 2 lR 1.弧长公式： 2.扇形面积公式： 注意： (1)两个公式的联系和区别； (2)两个公式的逆向应用. 例4 圆锥形烟囱帽（图3-54）的母线长为80cm，高 为38.7cm. （1）求这个烟囱帽的面积（精确到103cm). （2）以1:40的比例画出这个烟囱帽的展开图． 解（1）∵l=80cm，h=38.7cm， ∴S侧=πrl=π×70×80≈1.8×104(cm2). 答：烟囱帽的面积约1.8×104cm2. 2 2 2 280 38.7 70( )r l h cm      ， （2）烟囱帽的展开图的扇形圆心角为 按1:40的比例画这个烟囱帽的展开图，如图3-55. 70360 360 315 . 80 r l          1.将圆柱形纸筒的侧面沿虚线剪开，得到什么平 面图形？ 2.将圆锥形冰淇淋纸筒的侧面沿虚线剪开，得到 什么平面图形？ 3.沿图中的红线将无盖的正方体纸盒剪开，得到 什么平面图形？ 如图，哪一个是棱锥侧面展开图？ 1、直棱柱与圆柱、圆锥表面展开图的概念； 2、正确判断平面图形能否折叠围成立体图形； 3、会画直棱柱的表面展开图； 4、表面展开图的应用.