江西专版2020中考数学复习方案第四单元图形的初步认识与三角形第16课时三角形的基本知识及全等三角形课件 34页

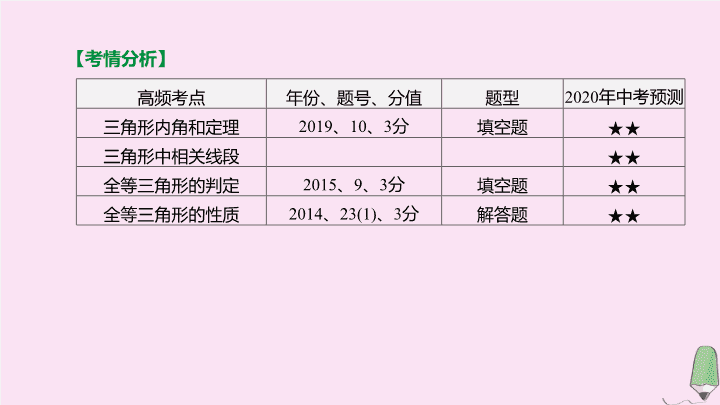
第 16 课时 三角形的基本知识及全等三角形 第四单元　图形的初步认识与三角形 【 考情分析 】 高频考点 年份、题号、分值 题型 2020 年中考预测 三角形 内角 和定理 2019 、 10 、 3 分 填空题 ★★ 三角形 中相关 线段 ★★ 全等三角形 的判定 2015 、 9 、 3 分 填空题 ★★ 全等三角形 的性质 2014 、 23(1) 、 3 分 解答题 ★★ 考点一　三角形的分类及三角形有关角的性质 考点聚焦 等边三角形 钝角三角形 2 . 三角形的内角和 : 三角形三个内角的和等于 ③ 　　　　 .  180° 3 . 三角形外角的性质 : (1) 三角形的一个外角 ④ 　　　　 任何一个和它不相邻的内角 ;  (2) 三角形的一个外角 ⑤ 　　　　 与它不相邻的两个内角之和 .  大于 等于 考点二　三角形有关边及重要线段的性质 1 . 三角形三边关系 三角形的任意两边之和 ⑥ 　　　　 第三边 ; 任意两边之差 ⑦ 　　　　 第三边 .  大于 小于 名称 图形 性质 重要结论 中线 BD= ⑧ 　　　 = ⑨ 　　　 BC  　 三角形的三条中线的交点在三角形 的 ⑩ 　　　　 部 , 中线将三角形分成两个面积相等的三角形   高线 AD ⊥ ⑪ 　　 , 即 ∠ ADB = ⑫ 　　　　 = 90°  　 ⑬ 　　　　 三角形的三条高的交点在三角形的内部 ; ⑭ 　　　　 三角形的三条高的交点是直角顶点 ; ⑮ 　　　　 三角形的三条高所在直线的交点在三角形的外部 , 这个点称为垂心   2 . 三角形中的重要线段 DC 内 BC ∠ ADC 锐角 直角 钝角 （续表） ∠ 2 内 DE EC DC 内 考点三　全等三角形的性质 1 . 能够完全重合的两个图形就是 ㉓ 　　　　　 . 能够完全重合的两个三角形就是 ㉔ 　　　　　　 .  2 . 全等三角形的对应边 ㉕ 　　　　 , 对应角 ㉖ 　　　　　 .  3 . 全等三角形的对应线段 ( 对应边上的中线、对应边上的高、对应角的平分线 ) ㉗ 　　　　　 , 周长相等 , 面积相等 .  全等图形 全等三角形 相等 相等 相等 考点四　全等三角形的判定 1 . 三角形全等的判定方法 : SAS, ㉘ 　　　　 , ㉙ 　 　　 , ㉚ 　　　　 .  2 . 两个直角三角形全等的判定方法除了一般的三角形全等的判定方法之外 , 还有 ㉛ 　　　　 .  ASA SSS AAS HL 角平分线的性质 角平分线的判定 　 角平分线上的点到角两边的距离 ㉜ 　　　　   　 角的内部到角两边距离相等的点 在 ㉝ 　　 　　　 上   考点五　角平分线的性质和判定 相等 角的平分线 题组一　必会题 对点演练 1 . 在 △ ABC 中 , ∠ A= 20°, ∠ B= 60°, 则 △ ABC 的形状是 ( 　　 ) A . 等边三角形 B . 锐角三角形 C . 直角三角形 D . 钝角三角形 D 2 . 如图 16-1, CE 是 △ ABC 的外角∠ ACD 的平分线 , 若∠ B= 35°, ∠ ACE= 60°, 则∠ A= ( 　　 ) A . 35° B . 95° C . 85° D . 75° 图 16-1 [ 答案 ] C 　 [ 解析 ] ∵ CE 是∠ ACD 的平分线 , ∴∠ ACD= 60°×2 = 120° . 又∵∠ ACD 是 △ ABC 的外角 , ∴∠ ACD= ∠ A + ∠ B , ∴∠ A= ∠ ACD - ∠ B= 120°-35° = 85°, 故选 C . 3 . [2019· 徐州 ] 下列长度的三条线段 , 能组成三角形的是 ( 　　 ) A . 2,2,4 B . 5,6,12 C . 5,7,2 D . 6,8,10 D 图 16-2 C 5 . [2019· 齐齐哈尔 ] 如图 16-3, 已知在 △ ABC 和 △ DEF 中 , ∠ B= ∠ E , BF=CE , 点 B , F , C , E 在同一 条直线上 , 若使 △ ABC ≌△ DEF , 则还需添加的一个条件是 　 　 　　 . ( 只填一个即可 )  图 16-3 AB=DE ( 答案不唯一 ) 题组二　易错题 【 失分点 】 混淆三角形中位线与中线 , 涉及三角形的边长或周长的计算时忽略三角形三边关系 . 6 . 如图 16-4, DE 是 △ ABC 的中位线 , 点 F 在 DE 上 , 且∠ AFC= 90°, 若 AC= 10, BC= 16, 则 DF 的长为 ( 　　 ) A . 5 B . 3 C . 8 D . 10 图 16-4 [ 答案 ] B 7 . 四根长度分别为 3,4,6, x ( x 为正整数 ) 的木棒 , 从中任取三根 , 首尾顺次相接都能组成一个三角形 , 则组成的三角形中周长最小为 　　　　 .  [ 答案 ] 11 　 [ 解析 ] 其中任意三根的组合有 3,4,6; 3,4, x ; 3,6, x ; 4,6, x 共四种情况 , 由题意 : 从中任取三根 , 首尾顺次相接都能组成一个三角形 , 可得 3