江西专版2020中考数学复习方案第五单元四边形第23课时菱形正方形课件 49页

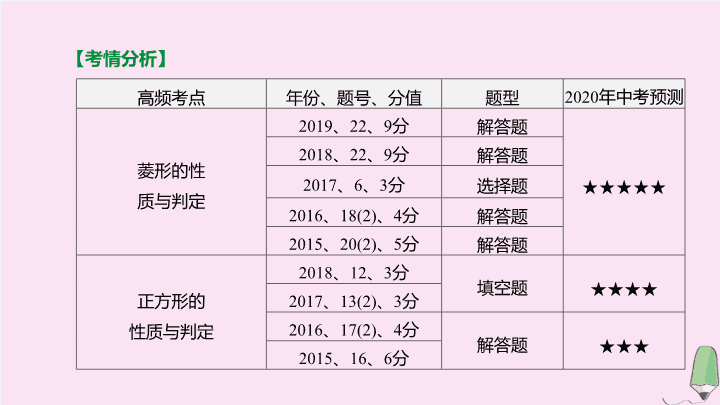
第 23 课时 菱形、正方形 第五单元　四边形 【 考情分析 】 高频考点 年份、题号、分值 题型 2020 年中考预测 菱形的性 质与判定 2019 、 22 、 9 分 解答题 ★★★★★ 2018 、 22 、 9 分 解答题 2017 、 6 、 3 分 选择题 2016 、 18(2) 、 4 分 解答题 2015 、 20(2) 、 5 分 解答题 正方形的 性质与判定 2018 、 12 、 3 分 填空题 ★★★★ 2017 、 13(2) 、 3 分 2016 、 17(2) 、 4 分 解答题 ★★★ 2015 、 16 、 6 分 定义 有一组邻边相等的平行四边形叫做菱形 性质 (1) 边 : 四条边都 ① 　　　　 , 对边平行 ;  (2) 角 : 对角相等 ; (3) 对角线 : 对角线 ② 　　　 , 并且 每一条对角线平分 ③ 　 　　　 ,  (4) 对称性 : 既是 ④ 　　　　 对称图形 , 又是 ⑤ 　　　　 对称图形 , 有 ⑥ 　　　　 条对称轴   考点一　菱形 考点聚焦 相等 互相垂直且平分 一组对角 轴 中心 2 ( 续表 ) 相等 相等 互相垂直 考点二　正方形 定义 　 有一组邻边相等且一个角是直角的平行四边形叫做正方形 性质 (1) 边 : 四条边都 ⑩ 　　　　 , 对边平行 ;  (2) 角 : 四个角都是 ⑪ 　　　　 ;  (3) 对角线 : 对角线互相垂直平分且 ⑫ 　　　　 , 每一条对角线都 平分 ⑬ 　　　 　 ( 对角线与边的夹角为 45°);  (4) 对称性 : 既是 ⑭ 　　　　 对称图形又是 ⑮ 　　　　 对称图形 , 有 ⑯ 　　　　 条对称轴   相等 直角 相等 一组对角 中心 轴 4 ( 续表 ) 直角 相等 相等 直角 相等且互相垂直 相等且互相垂直平分 　 【 温馨提示 】 平行四边形、矩形、菱形、正方形四者之间的关系 : 图 23-1 考点三　中点四边形 顺次连接四边形各边中点所得的四边形 , 我们称之为中点四边形 . 中点四边形形状的判定依据主要是三角形的中位线定理 . 常见结论如下 : 原四边形的形状 中点四边形的形状 任意四边形 ㉓ __________________________ 平行四边形 平行四边形 矩形 菱形 菱形 ㉔ __________________________ 正方形 ㉕ __________________________ 平行四边形 矩形 正方形 题组一　必会题 对点演练 1 . [2019· 上饶铅山一模 ] 已知平行四边形 ABCD , 下列条件中 , 不能判定这个平行四边形为菱形的是 ( 　　 ) A .AC ⊥ BD B . ∠ ABD= ∠ ADB C .AB=CD D .AB=BC C 2 . [2019· 河北 ] 如图 23-2, 菱形 ABCD 中 , ∠ D= 150°, 则∠ 1 = ( 　　 ) A . 30° 　　 B . 25° C . 20° 　 　 D . 15° D 图 23-2 3 . 如图 23-3, 在正方形 ABCD 中 , 点 E , F 分别在 BC , CD 上 , BE=CF , 则图中与∠ AEB 相等的角的个数是 ( 　　 ) A . 1 B . 2 C . 3 D . 4 图 23-3 [ 答案 ] C 4 . [2019· 苏州 ] 如图 23-4, 菱形 ABCD 的对角线 AC , BD 交于点 O , AC= 4, BD= 16, 将 △ ABO 沿点 A 到点 C 的方向平移 , 得到 △ A'B'O' , 当点 A' 与点 C 重合时 , 点 A 与点 B' 之间的距离为 ( 　　 ) A . 6 B . 8 C . 10 D . 12 图 23-4 [ 答案 ] C 5 . [2019· 十堰 ] 如图 23-5, 已知菱形 ABCD 的对角线 AC , BD 交于点 O , E 为 BC 的中点 , 若 OE= 3, 则菱形的周长为 　　　　 .  图 23-5 24 题组二　易错题 【 失分点 】 运用菱形或正方形的性质时 , 由于对性质理解不清造成解题错误 ; 菱形、正方形的判定混淆 ; 不能合理运用菱形、正方形的性质解决有关证明或计算问题 . 6 . 满足下列条件的四边形不是正方形的是 ( 　　 ) A . 对角线互相垂直的矩形 B . 对角线相等的菱形 C . 对角线互相垂直且相等的四边形 D . 对角线互相垂直且相等的平行四边形 [ 答案 ] C 　 [ 解析 ]A . 对角线互相垂直的矩形是正方形 , 故正确 ; B . 对角线相等的菱形是正方形 , 故正确 ; C . 对角线互相垂直平分且相等的四边形是正方形 , 故错误 ; D . 对角线互相垂直且相等的平行四边形是正方形 , 故正确 . 7 . [2019· 雅安 ] 如图 23-6, 在四边形 ABCD 中 , AB=CD , AC , BD 是对角线 , E , F , G , H 分别是 AD , BD , BC , AC 的中点 , 连接 EF , FG , GH , HE , 则四边形 EFGH 的形状是 ( 　　 ) A . 平行四边形 B . 矩形 C . 菱形 D . 正方形 图 23-6 [ 答案 ] C 考向一　菱形的性质及判定 图 23-7 例 1 [2019· 宁波 ] 如图 23-7, 矩形 EFGH 的顶点 E , G 分别在菱形 ABCD 的边 AD , BC 上 , 顶点 F , H 在菱形 ABCD 的对角线 BD 上 . (1) 求证 : BG=DE ; (2) 若 E 为 AD 中点 , FH= 2, 求菱形 ABCD 的周长 . 解 :(1) 证明 : 在矩形 EFGH 中 , EH=FG , EH ∥ FG , ∴∠ GFH= ∠ EHF. ∵∠ BFG= 180°- ∠ GFH , ∠ DHE= 180°- ∠ EHF , ∴∠ BFG= ∠ DHE , 在菱形 ABCD 中 , AD ∥ BC , ∴∠ GBF= ∠ EDH , ∴ △ BGF ≌△ DEH (AAS), ∴ BG=DE. (2) 连接 EG. 在菱形 ABCD 中 , AD ∥ BC , AD=BC. ∵ E 为 AD 的中点 , ∴ AE=ED. ∵ BG=DE , ∴ AE=BG. 又∵ AE ∥ BG , ∴四边形 ABGE 是平行四边形 , ∴ AB=EG. 在矩形 EFGH 中 , EG=FH= 2, ∴ AB= 2, ∴菱形 ABCD 的周长为 8 . 图 23-7 例 1 [2019· 宁波 ] 如图 23-7, 矩形 EFGH 的顶点 E , G 分别在菱形 ABCD 的边 AD , BC 上 , 顶点 F , H 在菱形 ABCD 的对角线 BD 上 . (2) 若 E 为 AD 中点 , FH= 2, 求菱形 ABCD 的周长 . | 考向精练 | 图 23-8 1 . [2019· 江西 6 题 ] 图 23-8 是由 10 根完全相同的小棒拼接而成 , 请你再添 2 根与前面完全相同的小棒 , 拼接后的图形恰好有 3 个菱形的方法共有 ( 　　 ) A . 3 种 B . 4 种 C . 5 种 D . 6 种 [ 答案 ] D 　 [ 解析 ] 具体拼法有 6 种 , 如图 . 图 23-9 解 :(1) 当点 E 与点 B 重合时 , ∵四边形 AEFG 是菱形 , ∴∠ ABF= ∠ AEF= 180°- ∠ EAG= 180°-120° = 60° . ∵∠ ABC= 120°, ∴∠ CEF= ∠ ABC - ∠ ABF= 120°-60° = 60° . 故答案为 60 . 图 23-9 图 23-9 图 23-9 3 . [2015· 江西 20 题 ] (1) 如图 23-10 ① ,▱ ABCD 纸片中 , AD= 5, S ▱ ABCD = 15 . 过点 A 作 AE ⊥ BC , 垂足为 E , 沿 AE 剪下 △ ABE , 将它平移至 △ DCE' 的位置 , 拼成四边形 AEE'D , 则四边形 AEE'D 的形状为 ( 　　 ) A . 平行四边形 B . 菱形 C . 矩形 D . 正方形 (2) 如图 23-10 ② , 在 (1) 中的四边形纸片 AEE'D 中 , 在 EE' 上取一点 F , 使 EF= 4, 剪下 △ AEF , 将它平移至 △ DE'F' 的位置 , 拼成四边形 AFF'D. ①求证 : 四边形 AFF'D 是菱形 ; ②求四边形 AFF'D 的两条对角线的长 . 图 23-10 解 :(1)C 　 [ 解析 ] 由平移知 AE ∥ DE' , AE=DE' , ∴四边形 AEE'D 是平行四边形 . 又∵ AE ⊥ BC , ∴∠ AEE'= 90°, ∴四边形 AEE'D 是矩形 . 3 . [2015· 江西 20 题 ] (2) 如图 23-10 ② , 在 (1) 中的四边形纸片 AEE'D 中 , 在 EE' 上取一点 F , 使 EF= 4, 剪下 △ AEF , 将它平移至 △ DE'F' 的位置 , 拼成四边形 AFF'D. ①求证 : 四边形 AFF'D 是菱形 ; ②求四边形 AFF'D 的两条对角线的长 . 图 23-10 考向二　正方形的性质及判定 图 23-11 例 2 [2019· 杭州 ] 如图 23-11, 已知正方形 ABCD 的边长为 1, 正方形 CEFG 的面积为 S 1 , 点 E 在 DC 边上 , 点 G 在 BC 的延长线上 . 设以线段 AD 和 DE 为邻边的矩形的面积为 S 2 , 且 S 1 =S 2 . (1) 求线段 CE 的长 ; (2) 若点 H 为 BC 边的中点 , 连接 HD , 求证 : HD=HG. 图 23-11 例 2 [2019· 杭州 ] 如图 23-11, 已知正方形 ABCD 的边长为 1, 正方形 CEFG 的面积为 S 1 , 点 E 在 DC 边上 , 点 G 在 BC 的延长线上 . 设以线段 AD 和 DE 为邻边的矩形的面积为 S 2 , 且 S 1 =S 2 . (2) 若点 H 为 BC 边的中点 , 连接 HD , 求证 : HD=HG. | 考向精练 | 图 23-12 [ 答案 ] D 2 . [2019· 青岛 ] 如图 23-13, 在正方形纸片 ABCD 中 , E 是 CD 的中点 , 将正方形纸片折叠 , 点 B 落在线段 AE 上的点 G 处 , 折痕为 AF. 若 AD= 4 cm, 则 CF 的长为 　　　　 cm .  图 23-13 3 . [2019· 长沙 ] 如图 23-14, 正方形 ABCD , 点 E , F 分别在 AD , CD 上 , 且 DE=CF , AF 与 BE 相交于点 G. (1) 求证 : BE=AF ; (2) 若 AB= 4, DE= 1, 求 AG 的长 . 图 23-14 解 :(1) 证明 : ∵四边形 ABCD 是正方形 , ∴∠ BAE= ∠ ADF= 90°, AB=AD=CD. ∵ DE=CF , ∴ AE=DF. 在 △ BAE 和 △ ADF 中 , AB=AD , ∠ BAE= ∠ ADF , AE=DF , ∴ △ BAE ≌△ ADF (SAS), ∴ BE=AF. 3 . [2019· 长沙 ] 如图 23-14, 正方形 ABCD , 点 E , F 分别在 AD , CD 上 , 且 DE=CF , AF 与 BE 相交于点 G. (2) 若 AB= 4, DE= 1, 求 AG 的长 . 图 23-14 考向三　中点四边形 图 23-15 例 3 [2017· 江西 6 题 ] 如图 23-15, 任意四边形 ABCD 中 , E , F , G , H 分别是 AB , BC , CD , DA 上的点 , 对于四边形 EFGH 的形状 , 某班学生在一次数学活动课中 , 通过动手实践 , 探索出如下结论 , 其中错误的是 ( 　　 ) A . 当 E , F , G , H 是各边中点 , 且 AC=BD 时 , 四边形 EFGH 为菱形 B . 当 E , F , G , H 是各边中点 , 且 AC ⊥ BD 时 , 四边形 EFGH 为矩形 C . 当 E , F , G , H 不是各边中点时 , 四边形 EFGH 可以为平行四边形 D . 当 E , F , G , H 不是各边中点时 , 四边形 EFGH 不可能为菱形 [ 答案 ] D | 考向精练 | 1 . [2019· 娄底 ] 顺次连接菱形四边中点得到的四边形是 ( 　　 ) A . 平行四边形 B . 菱形 C . 矩形 D . 正方形 C 2 . [2019· 北京 ] 在矩形 ABCD 中 , M , N , P , Q 分别为边 AB , BC , CD , DA 上的点 ( 不与端点重合 ) . 对于任意矩形 ABCD , 下面四个结论中 , ①存在无数个四边形 MNPQ 是平行四边形 ; ②存在无数个四边形 MNPQ 是矩形 ; ③存在无数个四边形 MNPQ 是菱形 ; ④至少存在一个四边形 MNPQ 是正方形 . 所有正确结论的序号是 　　　　 .  [ 答案 ] ①②③ 　 [ 解析 ] 如图 , 四边形 ABCD 是矩形 , 连接 AC , BD 交于点 O , 过点 O 的直线 MP 和 QN , 分别交 AB , BC , CD , AD 于 M , N , P , Q , 则四边形 MNPQ 是平行四边形 , 存在无数个四边形 MNPQ 是平行四边形 , 故①正确 ; 如图 , 当 PM=QN 时 , 四边形 MNPQ 是矩形 , 故存在无数个四边形 MNPQ 是矩形 , 故②正确 ; 如图 , 当 PM ⊥ QN 时 , 存在无数个四边形 MNPQ 是菱形 , 故③正确 ; 当四边形 MNPQ 是正方形时 , MQ=PQ , 则 △ AMQ ≌△ DQP , ∴ AM=QD , AQ=PD , 易知 △ PDQ ≌△ MBN , ∴ PD=BM , ∴ AB=AD , ∴四边形 ABCD 是正方形与任意矩形 ABCD 矛盾 , 故④错误 . 故填①②③ . 图 23-16