2020九年级数学下册 第27章 内切圆、外接圆 4页

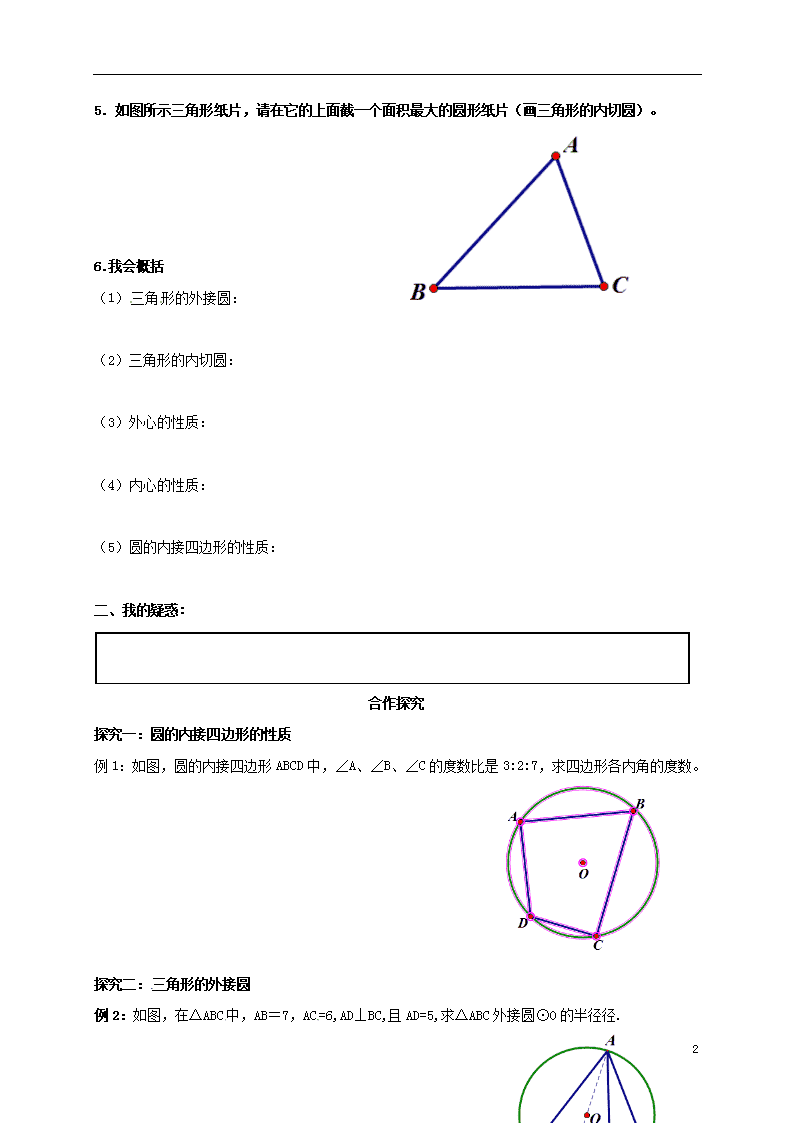
导 学 案 装 订 线 ‎ ‎27.2.3内切圆、外接圆 ‎【学习目标】 ‎ ‎1.知道三角形的内心和外心，掌握圆的内接四边形性质。‎ ‎2.会用内心、外心、圆的内接四边形性质解决问题。‎ ‎3.形成严密的思维习惯。‎ ‎【重点】用内心、外心、圆的内接四边形性质解决问题。‎ ‎【难点】用内心、外心、圆的内接四边形性质解决问题。‎ ‎【使用说明与学法指导】‎ 先预习课本P43、P47-48、P54圆的内接四边形、外心和内心内容，勾画重点，独立完成导学案，疑惑随时记录在课本或预习案上，准备课上讨论质疑；‎ 预 习 案 一、预习导学：‎ ‎1.过一点可以画多少个圆？‎ ‎2.过两点可以画多少个圆，圆心在哪里？‎ ‎3.过三点一定可以画出一个圆吗，说一说怎样的三点可以画圆？‎ ‎4.画出不在同一直线上的三点的圆？‎ 4‎ ‎5. 如图所示三角形纸片，请在它的上面截一个面积最大的圆形纸片（画三角形的内切圆）。‎ ‎6.我会概括 ‎（1）三角形的外接圆：‎ ‎（2）三角形的内切圆：‎ ‎（3）外心的性质：‎ ‎（4）内心的性质：‎ ‎（5）圆的内接四边形的性质：‎ 二、我的疑惑:‎ 合作探究 探究一：圆的内接四边形的性质 例1：如图，圆的内接四边形ABCD中，∠A、∠B、∠C的度数比是3:2:7，求四边形各内角的度数。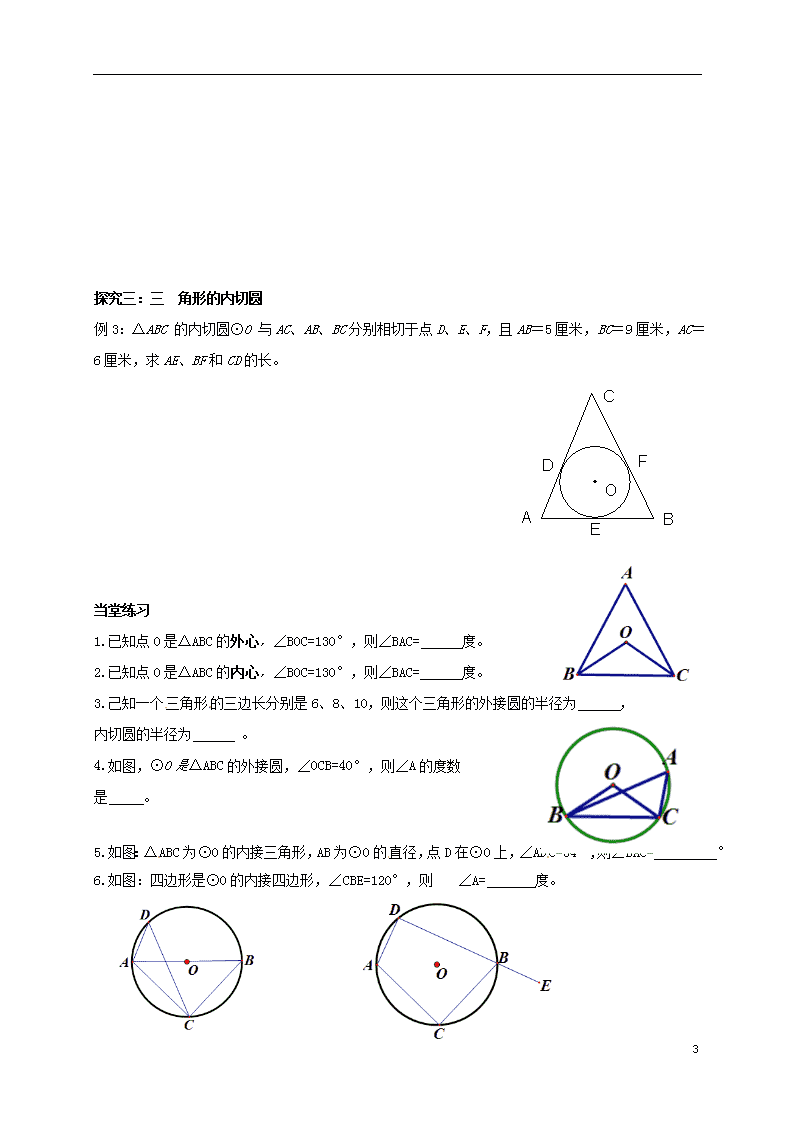‎ 探究二：三角形的外接圆 例2：如图，在△ABC中，AB＝7，AC=6,AD⊥BC,且AD=5,求△ABC外接圆⊙O的半径径.‎ 4‎ 探究三：三 角形的内切圆 例3：△ABC 的内切圆⊙O 与AC、AB、BC分别相切于点D、E、F，且AB＝‎5厘米，BC＝‎9厘米，AC＝‎6厘米，求AE、BF和CD的长。‎ 当堂练习 ‎1.已知点O是△ABC的外心，∠BOC=130°，则∠BAC= 度。‎ ‎2.已知点O是△ABC的内心，∠BOC=130°，则∠BAC= 度。‎ ‎3.己知一个三角形的三边长分别是6、8、10，则这个三角形的外接圆的半径为 ，‎ 内切圆的半径为 。‎ ‎4.如图，⊙O是△ABC的外接圆，∠OCB=40°，则∠A的度数 是 。‎ ‎5.如图：△ABC为⊙O的内接三角形，AB为⊙O的直径，点D在⊙O上，∠ADC=54°,则∠BAC= °‎ ‎6.如图：四边形是⊙O的内接四边形，∠CBE=120°，则 ∠A= 度。 ‎ 4‎ ‎【课堂小结】‎ ‎1.知识方面：‎ ‎2.数学思想方法：‎ 4‎