江西专版2020中考数学复习方案第四单元图形的初步认识与三角形课时训练19图形的相似 8页

课时训练(十九)　图形的相似 ‎(限时:45分钟)‎ ‎|夯实基础|‎ ‎1.如图K19-1,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若AB=3,DE=2,BC=6,则EF= (　　)‎ 图K19-1‎ A.‎18‎‎5‎ B.‎12‎‎5‎ C.4 D.9‎ ‎2.已知△ABC∽△DEF,若△ABC与△DEF的相似比为‎3‎‎4‎,则△ABC与△DEF对应中线的比为 (　　)‎ A.‎3‎‎4‎ B.‎4‎‎3‎ C.‎9‎‎16‎ D.‎‎16‎‎9‎ ‎3.[2019·重庆B卷]下列命题是真命题的是 (　　)‎ A.如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为2∶3‎ B.如果两个三角形相似,相似比为4∶9,那么这两个三角形的周长比为4∶9‎ C.如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为2∶3‎ D.如果两个三角形相似,相似比为4∶9,那么这两个三角形的面积比为4∶9‎ ‎4.[2018·义乌]学校门口的栏杆如图K19-2,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4 m,AB=1.6 m,CO=1 m,则栏杆C端应下降的垂直距离CD为 (　　)‎ 图K19-2‎ A.0.2 m B.0.3 m C.0.4 m D.0.5 m ‎5.[2019·眉山]如图K19-3,一束光线从点A(4,4)出发,经y轴上的点C反射后,经过点B(1,0),则点C的坐标是 (　　)‎ 图K19-3‎ A.0,‎1‎‎2‎ B.0,‎4‎‎5‎ C.(0,1) D.(0,2)‎ 8‎ ‎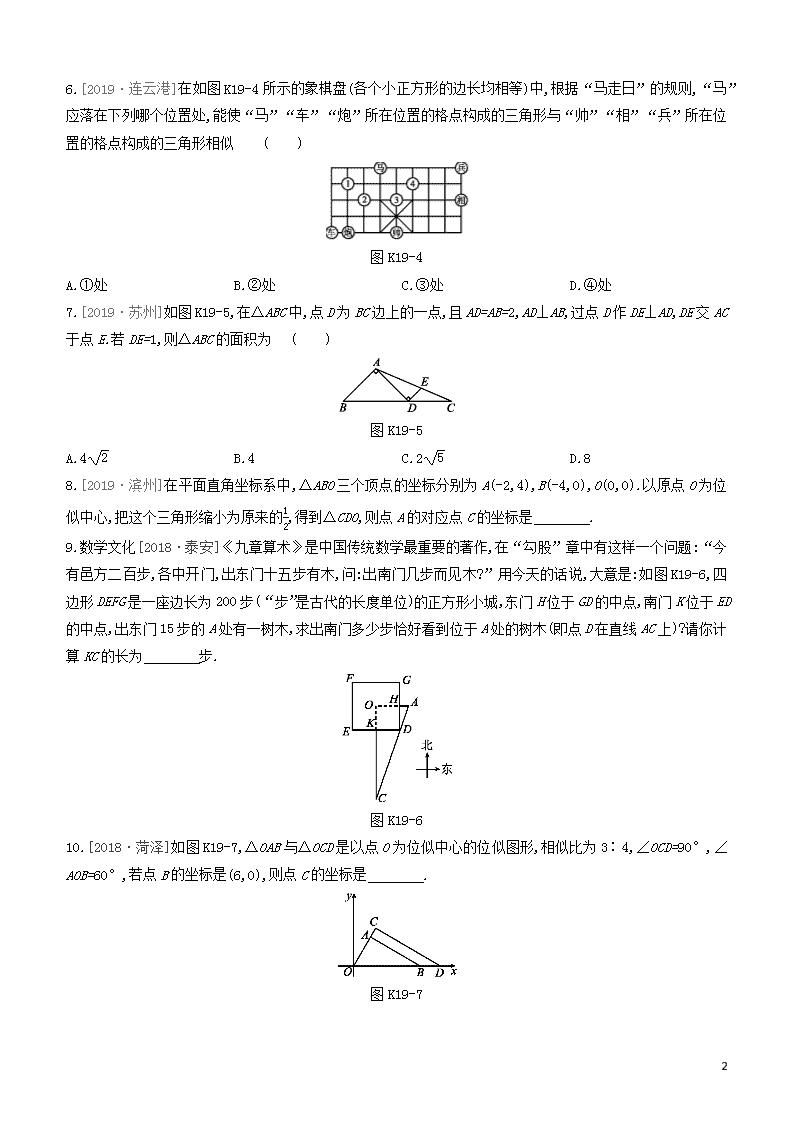6.[2019·连云港]在如图K19-4所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”“车”“炮”所在位置的格点构成的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似 (　　)‎ 图K19-4‎ A.①处 B.②处 C.③处 D.④处 ‎7.[2019·苏州]如图K19-5,在△ABC中,点D为BC边上的一点,且AD=AB=2,AD⊥AB,过点D作DE⊥AD,DE交AC于点E.若DE=1,则△ABC的面积为 (　　)‎ 图K19-5‎ A.4‎2‎ B.4 C.2‎5‎ D.8‎ ‎8.[2019·滨州]在平面直角坐标系中,△ABO三个顶点的坐标分别为A(-2,4),B(-4,0),O(0,0).以原点O为位似中心,把这个三角形缩小为原来的‎1‎‎2‎,得到△CDO,则点A的对应点C的坐标是　　　　. ‎ ‎9.数学文化[2018·泰安]《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图K19-6,四边形DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上)?请你计算KC的长为　　　　步. ‎ 图K19-6‎ ‎10.[2018·菏泽]如图K19-7,△OAB与△OCD是以点O为位似中心的位似图形,相似比为3∶4,∠OCD=90°,∠AOB=60°,若点B的坐标是(6,0),则点C的坐标是　　　　. ‎ 图K19-7‎ 8‎ ‎11.[2019·黄冈]如图K19-8,Rt△ABC中,∠ACB=90°,以AC为直径的☉O交AB于点D,过点D作☉O的切线交BC于点E,连接OE.‎ ‎(1)求证:△DBE是等腰三角形;‎ ‎(2)求证:△COE∽△CAB.‎ 图K19-8‎ ‎12.[2019·凉山州]如图K19-9,∠ABD=∠BCD=90°,DB平分∠ADC,过点B作BM∥CD交AD于M.连接CM交DB于N.‎ ‎(1)求证:BD2=AD·CD;‎ ‎(2)若CD=6,AD=8,求MN的长.‎ 图K19-9‎ 8‎ ‎|拓展提升|‎ ‎13.[2019·常德]在等腰三角形ABC中,AB=AC,作CM⊥AB交AB于点M,BN⊥AC交AC于点N.‎ ‎(1)在图K19-10①中,求证:△BMC≌△CNB;‎ ‎(2)在图K19-10②中的线段CB上取一动点P,过P作PE∥AB交CM于点E,作PF∥AC交BN于点F,求证:PE+PF=BM;‎ ‎(3)在图K19-10③中,动点P在线段CB的延长线上,类似(2)过P作PE∥AB交CM的延长线于点E,作PF∥AC交NB的延长线于点F,求证:AM·PF+OM·BN=AM·PE.‎ 图K19-10‎ 8‎ ‎【参考答案】‎ ‎1.C　2.A　3.B ‎4.C　[解析]∵AB⊥BD,CD⊥BD,∴∠ABO=∠CDO=90°.又∵∠AOB=∠COD(对顶角相等),∴△AOB∽△COD,∴AOCO=ABCD,即‎4‎‎1‎=‎1.6‎CD,∴CD=0.4 m.‎ ‎5.B　[解析]过点A作AD⊥y轴于点D,如图.‎ ‎∵∠ADC=∠COB=90°,∠ACD=∠BCO,∴△OBC∽△DAC,∴OCOB=DCAD,即OC‎1‎=‎4-OC‎4‎,解得OC=‎4‎‎5‎,∴点C0,‎4‎‎5‎.故选B.‎ ‎6.B　[解析]由网格得,“帅”“相”“兵”所在位置的格点构成的三角形的三边的长分别为2,2‎5‎,4‎2‎;‎ ‎“车”“炮”之间的距离为1,“炮”“②”之间的距离为‎5‎,“车”“②”之间的距离为2‎2‎.∵‎5‎‎2‎‎5‎=‎2‎‎2‎‎4‎‎2‎=‎1‎‎2‎,其他三处均不满足相似的条件,‎ ‎∴马应该落在②的位置.故选B.‎ ‎7.B　[解析]∵AB⊥AD,AD⊥DE,∴∠BAD=∠ADE=90°,∴DE∥AB,∴△CED∽△CAB.∵DE=1,AB=2,即DE∶AB=1∶2,∴S△DEC∶S△ACB=1∶4,∴S四边形ABDE∶S△ACB=3∶4.∵S四边形ABDE=S△ABD+S△ADE=‎1‎‎2‎×2×2+‎1‎‎2‎×2×1=2+1=3,∴S△ACB=4.故选B.‎ ‎8.(-1,2)或(1,-2).‎ ‎9.‎2000‎‎3‎　[解析]∵四边形DEFG是正方形,∴DG∥KC,∴△AHD∽△AOC,∴AHAO=HDOC,即‎15‎‎15+100‎=‎100‎‎100+KC,解得KC=‎2000‎‎3‎.‎ ‎10.(2,2‎3‎)　[解析]如图,过点A作AE⊥x轴于E.‎ ‎∵∠OCD=90°,△OAB与△OCD位似,∴∠OAB=90°.∵∠AOB=60°,∴∠ABO=∠OAE=30°.‎ ‎∵点B的坐标是(6,0),∴AO=‎1‎‎2‎OB=3,∴OE=‎1‎‎2‎OA=‎3‎‎2‎,∴AE=OA‎2‎-OE‎2‎=‎3‎‎2‎‎-(‎3‎‎2‎)‎‎ ‎‎2‎=‎3‎‎3‎‎2‎,‎ ‎∴A‎3‎‎2‎,‎3‎‎3‎‎2‎.‎ ‎∵△OAB与△OCD是以点O为位似中心的位似图形,相似比为3∶4,‎ ‎∴点C的坐标为‎3‎‎2‎‎×‎‎4‎‎3‎,‎3‎‎3‎‎2‎‎×‎‎4‎‎3‎,即(2,2‎3‎).‎ ‎11.证明:(1)连接OD.‎ ‎∵DE是☉O的切线,∴∠ODE=90°,‎ ‎∴∠ADO+∠BDE=90°.‎ 8‎ ‎∵∠ACB=90°,‎ ‎∴∠CAB+∠CBA=90°.‎ ‎∵OA=OD,∴∠CAB=∠ADO,∴∠BDE=∠CBA,‎ ‎∴EB=ED,∴△DBE是等腰三角形.‎ ‎(2)∵∠ACB=90°,AC是☉O的直径,‎ ‎∴CB是☉O的切线.‎ ‎∵DE是☉O的切线,∴DE=EC.‎ ‎∵EB=ED,∴EC=EB.‎ ‎∵OA=OC,∴OE∥AB,‎ ‎∴△COE∽△CAB.‎ ‎12.解:(1)证明:∵DB平分∠ADC,‎ ‎∴∠ADB=∠BDC.‎ 又∵∠ABD=∠BCD=90°,‎ ‎∴△DAB∽△DBC,‎ ‎∴BDCD=ADBD,∴BD2=AD·CD.‎ ‎(2)由(1)可知,BD2=AD·CD.‎ ‎∵CD=6,AD=8,∴BD=4‎3‎.‎ 又AD=8,‎ ‎∴AB=AD‎2‎-BD‎2‎=‎8‎‎2‎‎-(4‎‎3‎‎)‎‎2‎=4,‎ ‎∴AB=‎1‎‎2‎AD,‎ ‎∴∠ADB=30°,∴∠BDC=∠ADB=30°.‎ 又∠ABD=∠BCD=90°,‎ ‎∴∠A=∠DBC=60°.‎ ‎∵BM∥CD,‎ ‎∴∠MBD=∠BDC=30°,‎ ‎∴∠ABM=∠ABD-∠MBD=60°,‎ ‎∴△ABM是等边三角形,故BM=AB=4.‎ ‎∵△ABD∽△BCD,∴ABBC=DBCD,‎ ‎∴BC=AB·CDDB=‎4×6‎‎4‎‎3‎=2‎3‎.‎ ‎∵BM∥CD,∴∠CBM=180°-∠BCD=90°,‎ ‎∴CM=BM‎2‎+CB‎2‎=‎4‎‎2‎‎+(2‎‎3‎‎)‎‎2‎=2‎7‎.‎ ‎∵BM∥CD,∴△BMN∽△DCN,‎ ‎∴MNCN=MBCD=‎4‎‎6‎=‎2‎‎3‎.‎ 又CN+MN=CM=2‎7‎,‎ 8‎ ‎∴MN=‎4‎‎5‎ ‎7‎.‎ ‎13.解:(1)证明:∵AB=AC,∴∠ABC=∠ACB.‎ ‎∵CM⊥AB,BN⊥AC,‎ ‎∴∠BMC=∠CNB=90°.‎ 又∵BC=BC,‎ ‎∴△BMC≌△CNB.‎ ‎(2)连接OP,如图①.‎ ‎∵PE∥AB,PF∥AC,‎ ‎∴∠BMC=∠PEC=90°,∠CNB=∠PFB=90°.‎ ‎∵S△BOC=S△BOP+S△COP,‎ ‎∴‎1‎‎2‎OC·BM=‎1‎‎2‎OB·PF+‎1‎‎2‎OC·PE.‎ ‎∵△BMC≌△CNB,∴∠OBC=∠OCB,‎ ‎∴OB=OC,‎ ‎∴PE+PF=BM.‎ ‎ (3)连接OP,如图②.‎ ‎∵S△BOC=S△COP-S△BOP,‎ ‎∴‎1‎‎2‎OC·BM=‎1‎‎2‎OC·PE-‎1‎‎2‎OB·PF.‎ ‎∵OB=OC,∴PE-PF=BM.‎ ‎∵∠BMC=∠ANB=90°,∠MBO=∠NBA,‎ ‎∴△BOM∽△BAN,‎ ‎∴BMBN=OMAN,‎ ‎∴OM·BN=BM·AN=(PE-PF)·AN.‎ ‎∵AB=AC,BM=CN,∴AM=AN,‎ ‎∴OM·BN=(PE-PF)·AN=(PE-PF)·AM,‎ ‎∴AM·PF+OM·BN=AM·PE.‎ 8‎ 8‎