福建专版2020中考数学复习方案第六单元圆第33课时与圆有关的计算课件 39页

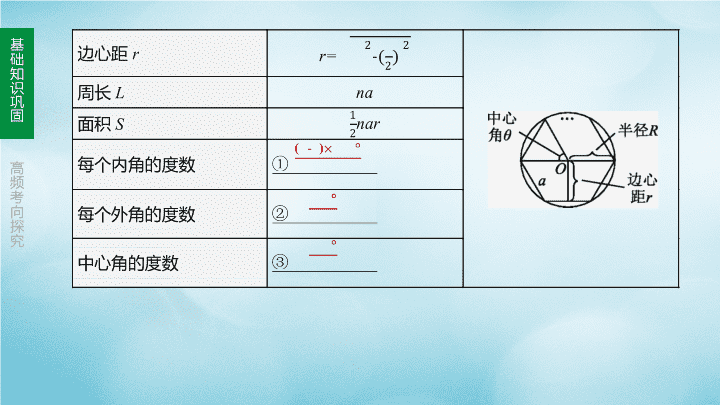
第 33 课时 与圆有关的计算 第六单元　圆 基 础 知 识 巩 固 高 频 考 向 探 究 考点一　正多边形和圆的相关计算 考点聚焦 设正n边形的外接圆半径为R,边长为a,边心距为r. 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 考点二　弧长与扇形面积公式 基 础 知 识 巩 固 高 频 考 向 探 究 考点三　阴影部分面积的计算 1.规则图形的面积,直接利用对应公式计算. 2.不规则图形的面积,要将图形的面积转化为可求图形的面积的和或差,常用方 法有:(1)割补法;(2)拼凑法;(3)等积转化法;(4)平移法;(5)旋转法. 基 础 知 识 巩 固 高 频 考 向 探 究 图形 圆锥简介 (1)h是圆锥的高; (2)l是圆锥的母线,其长为侧面展开后所得扇形的⑥　　　　;  (3)r是底面圆半径; (4)圆锥的侧面展开图是扇形,其弧长等于圆锥底面⑦ 　　 　  圆锥的侧面积 S侧=⑧　　　  圆锥的全面积 S全=S侧+S底=πrl+πr2 考点四　圆锥的侧面积与全面积 半径 圆的周长 πrl 基 础 知 识 巩 固 高 频 考 向 探 究 题组一　必会题 对点演练 1.若扇形的圆心角为90°,半径为6,则该扇形的弧长为　　　　.  2.一个扇形的半径为6,圆心角为120°,则该扇形的面积是　　　　.  3.[2019·南平质检]已知扇形的弧长为4π,半径为8,则此扇形的面积为　　　　.  3π 12π 16π 基 础 知 识 巩 固 高 频 考 向 探 究 图33-1 2π 基 础 知 识 巩 固 高 频 考 向 探 究 5.[2019·泉州石狮一模]若一个扇形的圆 心角为120°,面积为6π,则这个扇形的半径 为　　　　.  基 础 知 识 巩 固 高 频 考 向 探 究 题组二　易错题 【失分点】 未弄清圆锥侧面展开图的面积、弧长与圆锥的关系导致做题时出错. 6.已知圆锥的底面直径为4 cm,母线长为10 cm,则这个圆锥的侧面积是 (　　) A.20π cm2 B.20 cm2 C.40π cm2 D.40 cm2 A 基 础 知 识 巩 固 高 频 考 向 探 究 考向一　弧长的计算 [答案] 6π 　例1[2019·泰州]如图33-2,分别以正三角形的3 个顶点为圆心,边长为半径画弧,三段弧围成的 图形称为莱洛三角形.若正三角形的边长为 6 cm,则该莱洛三角形的周长为　　　　 cm.  图33-2 基 础 知 识 巩 固 高 频 考 向 探 究 | 考向精练 | 图33-3 基 础 知 识 巩 固 高 频 考 向 探 究 图33-4 2.[2019·泉州、晋江季延初级中学模拟]如图33-4,在扇形OAB中,∠AOB=100°,半 径OA=6,将扇形OAB沿过点A的直线折叠,点O恰好落在弧AB上的点D处,折痕交 OB于点C,则弧BD的长为　　　　.  基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 考向二　面积的计算 微专题 角度1　直接分割求面积 图33-5 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 【方法点析】可选择用割补法将不规则图形转化成常见的规则的图形进行计算. 基 础 知 识 巩 固 高 频 考 向 探 究 | 考向精练 | [2019·三明质检]如图33-6,在矩形ABCD中,AD=2,以点A为圆心,AD长为半径画 弧,交BC边于点E,若E恰为BC的中点,则图中阴影部分的面积为　　　　.  图33-6 基 础 知 识 巩 固 高 频 考 向 探 究 角度2　等积转化求面积 图33-7 基 础 知 识 巩 固 高 频 考 向 探 究 [答案]A 基 础 知 识 巩 固 高 频 考 向 探 究 | 考向精练 | 1.[2019·龙岩质检]如图33-8,AB是☉O的直径,点E是弧BF的中点,过点E的切线分 别交AF,AB的延长线于点D,C,若∠C=30°, ☉O的半径是2,则图中阴影部分的面 积是　　　　.  图33-8 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 图33-9 2.[2019·福建15题]如图33-9,边长为2的正方 形ABCD的中心与半径为2的☉O的圆心重 合,E,F分别是AD,BA的延长线与☉O的交点, 则图中阴影部分的面积为　　　　.(结果 保留π)  [答案] π-1 基 础 知 识 巩 固 高 频 考 向 探 究 角度3　与旋转有关的面积问题 图33-10 例4 如图33-10,C为半圆内一点,O为圆心,直径AB长为2 cm,∠BOC=60°, ∠BCO =90°,将△BOC绕圆心O逆时针旋转至△B'OC',使点C'落在OA上,则边BC扫过区域 (图中阴影部分)的面积为　　　　cm2.  基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 | 考向精练 | 如图33-11,将四边形ABCD绕顶点A顺时针旋 转45°至四边形AB'C'D'的位置,若AB=16 cm, 则图中阴影部分的面积为　　　　.  图33-11 [答案] 32π cm2 基 础 知 识 巩 固 高 频 考 向 探 究 考向三　运动路径的计算 图33-12 例5 如图33-12,矩形ABCD中,AB=4,BC=3,边CD在直线l上,将矩形ABCD沿直线 l作无滑动翻滚,当点A第一次翻滚到点A1的位置时,则点A经过的路线长为 　　　　.  基 础 知 识 巩 固 高 频 考 向 探 究 [答案] 6π 　 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 | 考向精练 | 图33-13 [答案] A　 基 础 知 识 巩 固 高 频 考 向 探 究 图33-14 2.[2018·安徽模拟]如图33-14,一个圆作滚动运动,它从A位置开始,滚过与它相同 的其他六个圆的上部,到达B位置.则该圆共滚过　　　　圈.  基 础 知 识 巩 固 高 频 考 向 探 究 考向四　圆与正多边形的相关计算 图33-15 基 础 知 识 巩 固 高 频 考 向 探 究 [答案] D 基 础 知 识 巩 固 高 频 考 向 探 究 | 考向精练 | 图33-16 B 基 础 知 识 巩 固 高 频 考 向 探 究 考向五　与圆锥的侧面展开图有关的问题 例7 (1)已知圆锥的母线长为4,底面半径 为2,则圆锥的侧面积为　　　　;  (2)将一个圆心角为120°,半径为6 cm的扇 形围成一个圆锥的侧面,则这个圆锥的底 面半径为　　　　;  (3)如果圆锥的底面周长是20π,侧面展开 后所得的扇形的圆心角为120°,则其侧面 积为　　　　(结果用含π的式子表示).  [答案] (1)8π　(2)2 cm　(3)300π 　 基 础 知 识 巩 固 高 频 考 向 探 究 | 考向精练 | 图33-17 1.如图33-17,在Rt△ABC中,AC=5 cm, BC= 12 cm,∠ACB=90°,把Rt△ABC绕BC所在 的直线旋转一周得到一个几何体,则这个 几何体的侧面积为 (　　) A.60π cm2 B.65π cm2 C.120π cm2 D.130π cm2 [答案] B 基 础 知 识 巩 固 高 频 考 向 探 究 2.若圆锥的侧面积是15π,母线长是5,则该圆 锥底面圆的半径是　　　　.  [答案] 3