2020年中考三轮冲刺复习培优同步练习：《三角形》（解析版） 43页

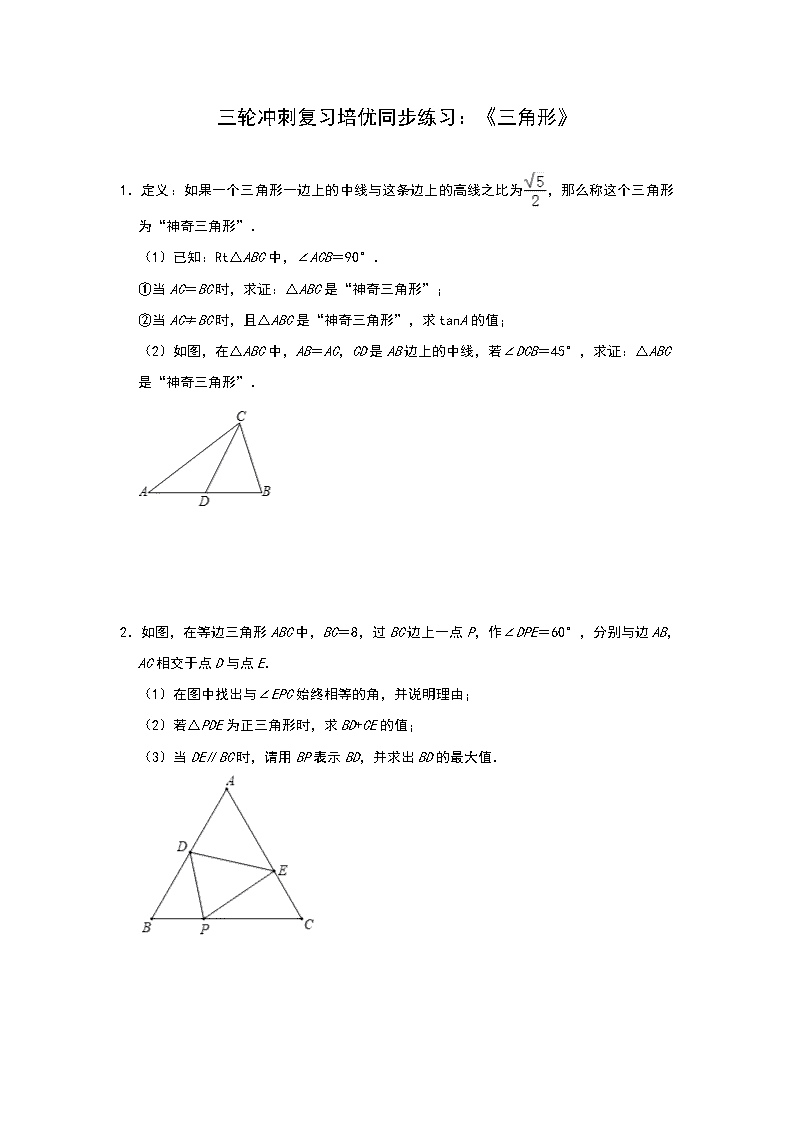
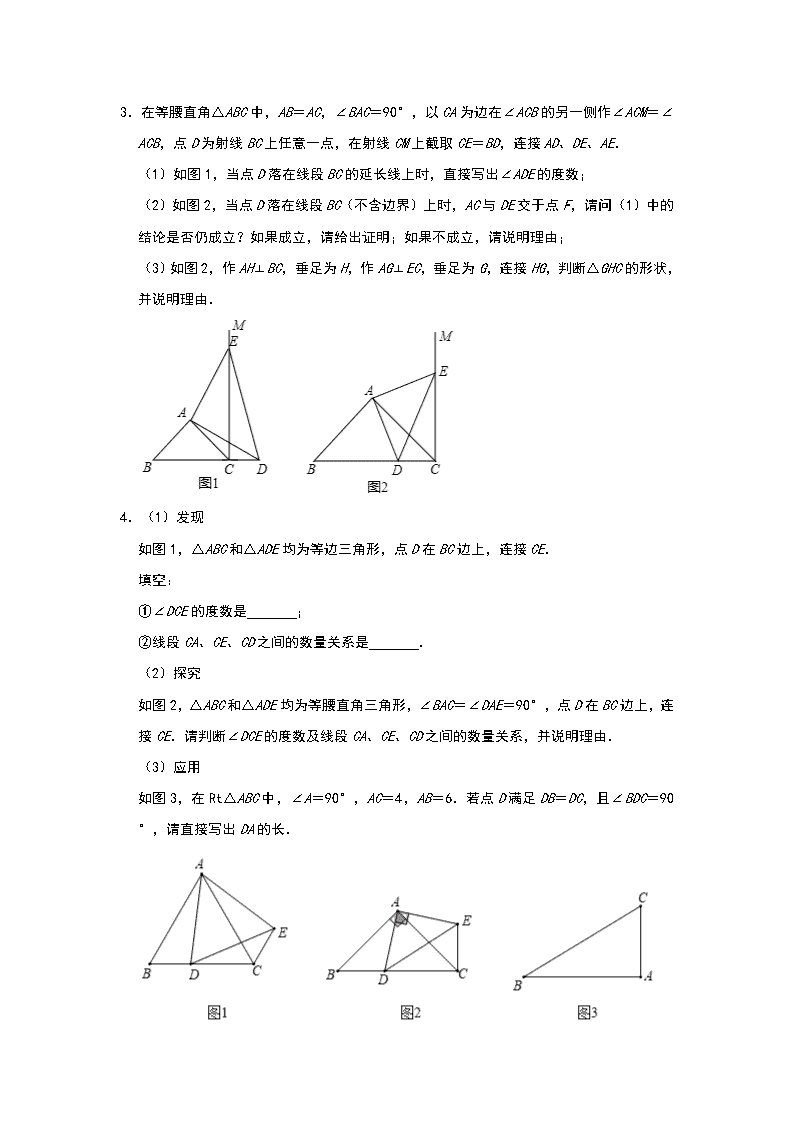
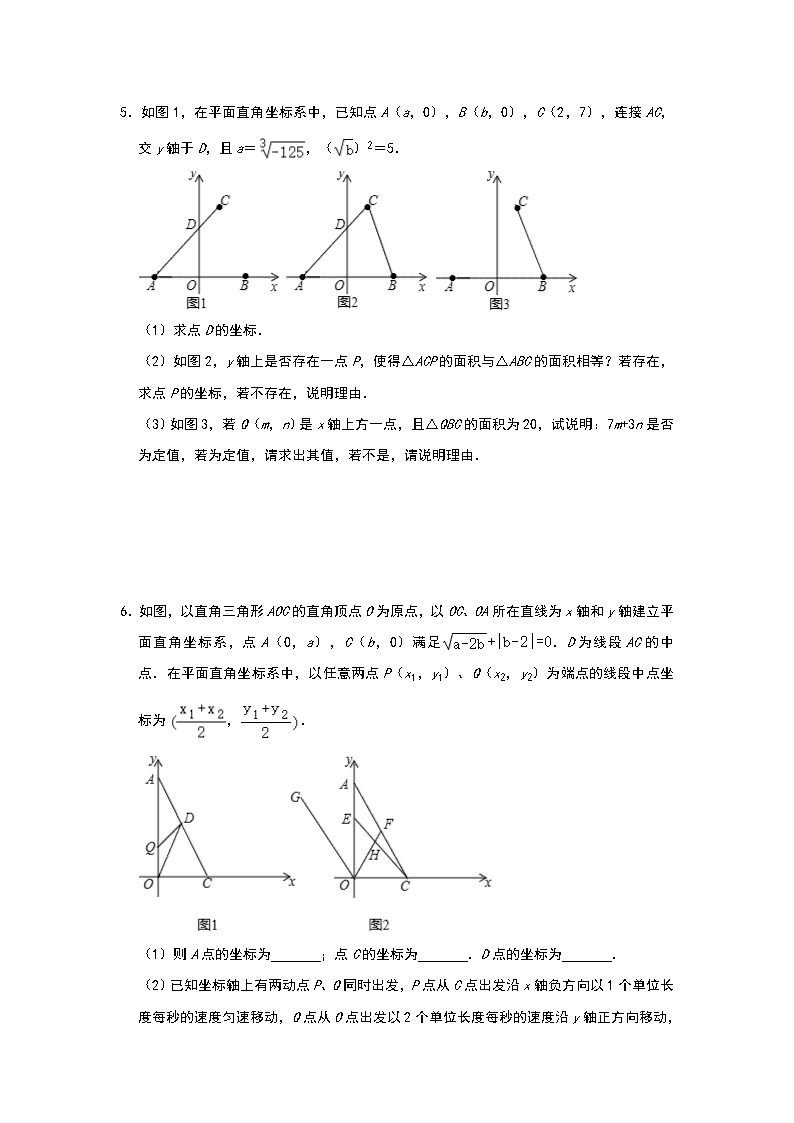
三轮冲刺复习培优同步练习：《三角形》‎ ‎1．定义：如果一个三角形一边上的中线与这条边上的高线之比为，那么称这个三角形为“神奇三角形”．‎ ‎（1）已知：Rt△ABC中，∠ACB＝90°．‎ ‎①当AC＝BC时，求证：△ABC是“神奇三角形”；‎ ‎②当AC≠BC时，且△ABC是“神奇三角形”，求tanA的值；‎ ‎（2）如图，在△ABC中，AB＝AC，CD是AB边上的中线，若∠DCB＝45°，求证：△ABC是“神奇三角形”．‎ ‎2．如图，在等边三角形ABC中，BC＝8，过BC边上一点P，作∠DPE＝60°，分别与边AB，AC相交于点D与点E．‎ ‎（1）在图中找出与∠EPC始终相等的角，并说明理由；‎ ‎（2）若△PDE为正三角形时，求BD+CE的值；‎ ‎（3）当DE∥BC时，请用BP表示BD，并求出BD的最大值．‎ ‎3．在等腰直角△ABC中，AB＝AC，∠BAC＝90°，以CA为边在∠ACB的另一侧作∠ACM＝∠ACB，点D为射线BC上任意一点，在射线CM上截取CE＝BD，连接AD、DE、AE．‎ ‎（1）如图1，当点D落在线段BC的延长线上时，直接写出∠ADE的度数；‎ ‎（2）如图2，当点D落在线段BC（不含边界）上时，AC与DE交于点F，请问（1）中的结论是否仍成立？如果成立，请给出证明；如果不成立，请说明理由；‎ ‎（3）如图2，作AH⊥BC，垂足为H，作AG⊥EC，垂足为G，连接HG，判断△GHC的形状，并说明理由．‎ ‎4．（1）发现 如图1，△ABC和△ADE均为等边三角形，点D在BC边上，连接CE．‎ 填空：‎ ‎①∠DCE的度数是　 　；‎ ‎②线段CA、CE、CD之间的数量关系是　 　．‎ ‎（2）探究 如图2，△ABC和△ADE均为等腰直角三角形，∠BAC＝∠DAE＝90°，点D在BC边上，连接CE．请判断∠DCE的度数及线段CA、CE、CD之间的数量关系，并说明理由．‎ ‎（3）应用 如图3，在Rt△ABC中，∠A＝90°，AC＝4，AB＝6．若点D满足DB＝DC，且∠BDC＝90°，请直接写出DA的长．‎ ‎5．如图1，在平面直角坐标系中，已知点A（a，0），B（b，0），C（2，7），连接AC，交y轴于D，且a＝，（）2＝5．‎ ‎（1）求点D的坐标．‎ ‎（2）如图2，y轴上是否存在一点P，使得△ACP的面积与△ABC的面积相等？若存在，求点P的坐标，若不存在，说明理由．‎ ‎（3）如图3，若Q（m，n）是x轴上方一点，且△QBC的面积为20，试说明：7m+3n是否为定值，若为定值，请求出其值，若不是，请说明理由．‎ ‎6．如图，以直角三角形AOC的直角顶点O为原点，以OC、OA所在直线为x轴和y轴建立平面直角坐标系，点A（0，a），C（b，0）满足．D为线段AC的中点．在平面直角坐标系中，以任意两点P（x1，y1）、Q（x2，y2）为端点的线段中点坐标为，．‎ ‎（1）则A点的坐标为　 　；点C的坐标为　 　．D点的坐标为　 　．‎ ‎（2）已知坐标轴上有两动点P、Q同时出发，P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动，Q点从O点出发以2个单位长度每秒的速度沿y 轴正方向移动，点Q到达A点整个运动随之结束．设运动时间为t（t＞0）秒．问：是否存在这样的t，使S△ODP＝S△ODQ，若存在，请求出t的值；若不存在，请说明理由．‎ ‎（3）点F是线段AC上一点，满足∠FOC＝∠FCO，点G是第二象限中一点，连OG，使得∠AOG＝∠AOF．点E是线段OA上一动点，连CE交OF于点H，当点E在线段OA上运动的过程中，的值是否会发生变化？若不变，请求出它的值；若变化，请说明理由．‎ ‎7．已知：如图，在平面直角坐标系中，点A（a，0）、B（0，b）、且|a+2|+（b+2a）2＝0，点P为x轴上一动点，连接BP；‎ ‎（1）求点A、B的坐标；‎ ‎（2）如图，在第一象限内作BC⊥AB且BC＝AB，连接CP，当CP⊥BC时，作CD⊥BP于点D，求线段CD的长度；‎ ‎（3）在第一象限内作BQ⊥BP且BQ＝BP，连接PQ，设P（p，0），直接写出S△PCQ＝　 　（用含p的式子表示）．‎ ‎8．在△ABC和△DBE中，CA＝CB，EB＝ED，点D在AC上．‎ ‎（1）如图1，若∠ABC＝∠DBE＝60°，求证：∠ECB＝∠A；‎ ‎（2）如图2，设BC与DE交于点F．当∠ABC＝∠DBE＝45°时，求证：CE∥AB；‎ ‎（3）在（2）的条件下，若tan∠DEC＝时，求的值．‎ ‎9．如图，在△ABC中，BC＝7cm，AC＝24cm，AB＝25cm，P点在BC上，从B点到C点运动（不包括C点），点P运动的速度为2cm/s；Q点在AC上从C点运动到A点（不包括A点），速度为5cm/s．若点P、Q分别从B、C同时运动，请解答下面的问题，并写出探索主要过程：‎ ‎（1）经过多少时间后，P、Q两点的距离为5cm？‎ ‎（2）经过多少时间后，S△PCQ的面积为15cm2？‎ ‎（3）用含t的代数式表示△PCQ的面积，并用配方法说明t为何值时△PCQ的面积最大，最大面积是多少？‎ ‎10．我们规定，三角形任意两边的“广益值”‎ 等于第三边上的中线和这边一半的平方差．如图1，在△ABC中，AO是BC边上的中线，AB与AC的“广益值”就等于AO2﹣BO2的值，可记为AB∇AC＝OA2﹣BO2．‎ ‎（1）在△ABC中，若∠ACB＝90°，AB∇AC＝81，求AC的值．‎ ‎（2）如图2，在△ABC中，AB＝AC＝12，∠BAC＝120°，求AB∇AC，BA∇BC的值．‎ ‎（3）如图3，在△ABC中，AO是BC边上的中线，S△ABC＝24，AC＝8，AB∇AC＝﹣64，求BC和AB的长．‎ ‎11．已知：等边△ABC中．‎ ‎（1）如图1，点M是BC的中点，点N在AB边上，满足∠AMN＝60°，求的值；‎ ‎（2）如图2，点M在AB边上（M为非中点，不与A、B重合），点N在CB的延长线上且∠MNB＝∠MCB，求证：AM＝BN．‎ ‎（3）如图3，点P为AC边的中点，点E在AB的延长线上，点F在BC的延长线上，满足∠AEP＝∠PFC，求的值．‎ ‎12．如图，等边△ABC的边长为15cm，现有两点M，N分别从点A，点B 同时出发，沿三角形的边顺时针运动，已知点M的速度为1cm/s，点N的速度为2cm/s．当点N第一次到达B点时，M，N同时停止运动 ‎（1）点M、N运动几秒后，M，N两点重合？‎ ‎（2）点M、N运动几秒后，△AMN为等边三角形？‎ ‎（3）当点M，N在BC边上运动时，能否得到以MN为底边的等腰三角形AMN？如存在，请求出此时M，N运动的时间．‎ ‎13．通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比例相互唯一确定，因此，边长与角的大小之间可以相互转化．类似地，可以在等腰三角形中建立边角之间的关系．我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图①，在△ABC中，AB＝AC，顶角A的正对记作sadA，这时sadA＝＝．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．‎ 根据上述角的正对定义，解下列问题：‎ ‎（1）sad60°＝　 　．‎ ‎（2）对于0°＜A＜180°，∠A的正对值sadA的取值范围是　 　．‎ ‎（3）如图②，已知∠C＝90°，sinA＝，其中∠A为锐角，试求sadA的值．‎ ‎14．如图，在Rt△ABC中，∠ACB＝90°，BC＝4，sin∠ABC＝，点D为射线BC 上一点，联结AD，过点B作BE⊥AD分别交射线AD、AC于点E、F，联结DF，过点A作AG∥BD，交直线BE于点G．‎ ‎（1）当点D在BC的延长线上时，如果CD＝2，求tan∠FBC；‎ ‎（2）当点D在BC的延长线上时，设AG＝x，S△DAF＝y，求y关于x的函数关系式（不需要写函数的定义域）；‎ ‎（3）如果AG＝8，求DE的长．‎ ‎15．如图，点O为平面直角坐标系的原点，三角形ABC中，∠BAC＝90°，AB＝m．顶点A，C的坐标分别为（1，0），（n，0），且|m﹣3|+（n﹣5）2＝0．‎ ‎（1）求三角形ABC的面积；‎ ‎（2）动点P从点C出发沿射线CA方向以每秒1个单位长度的速度运动，设点P的运动时间为t秒，连接PB，请用含t的式子表示三角形ABP的面积；‎ ‎（3）在（2）的条件下，当三角形ABP的面积为时，直线BP与y轴相交于点D，求点D的坐标．‎ ‎16．已知△ABC和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°．‎ ‎（1）若D为AB上一动点时（如图1），‎ ‎①求证：△ACD≌△BCE．‎ ‎②试求线段AD，BD，DE间满足的数量关系．‎ ‎（2）当点D在△ABC内部时（如图2），延长AD交BE于点F．‎ ‎①求证：AF⊥BE．‎ ‎②连结BD，当△BDE为等边三角形时，直接写出△DCE与△ABC的边长之比．‎ ‎17．如图，直角坐标系中，点A，B分别在x，y轴上，点B的坐标为（0，2），∠BAO＝30°．以AB为边在第一象限作等边△ABC，MN垂直平分OA，MA⊥AB．‎ ‎（1）求AB的长．‎ ‎（2）求证：MB＝OC．‎ ‎（3）如图2，连接MC交AB于点P．点P是否为MC的中点？请说明理由．‎ ‎18．在△ABC中，AB＝BC，∠A＝40°，BD⊥AC垂足为D．‎ ‎（1）填空：∠ABC＝　 　°；‎ ‎（2）E是线段BD上的动点，连结EC，将线段EC绕点E按顺时针方向旋转80°，点C的对应点是点F，连接CF，得到△CEF．‎ ‎①如图1，若点F在直线BD上，AB＝a，AC＝b，求EB+EC的值．‎ ‎②连结AF，直线AF与直线BC是否平行，为什么？‎ ‎19．如图，在平面直角坐标系中，点A（0，a），B（b，0），且a，b满足2a2+2ab+b2﹣8a+16＝0，点P为AB上一个动点（不与A，B）重合），连接OP．‎ ‎（1）直接写出a＝　 　，b＝　 　；‎ ‎（2）如图1，过点P作OP的垂线交过点A平行于x轴的直线于点C，若点，求点C的坐标；‎ ‎（3）如图2，以OP为斜边在OP右侧作等腰Rt△OPD，PD＝OD．连接BD，当点P从B向A运动过程中，△BOD的面积是否发生变化，请判断并说明理由．‎ ‎20．（1）如图①，小明同学作出△ABC两条角平分线AD，BE得到交点I，就指出若连接 CI，则CI平分∠ACB，你觉得有道理吗？为什么？‎ ‎（2）如图②，Rt△ABC中，AC＝5，AC＝12，AB＝13，△ABC的角平分线CD上有一点I，设点I到边AB的距离为d．（d为正实数）‎ 小季、小何同学经过探究，有以下发现：‎ 小季发现：d的最大值为．‎ 小何发现：当d＝2时，连接AI，则AI平分∠BAC．‎ 请分别判断小季、小何的发现是否正确？并说明理由．‎ 参考答案 ‎1．解：（1）①证明：如图，作AC边上的中线BM，‎ 设CM＝AM＝a，则BC＝AC＝2a，‎ ‎∵∠ACB＝90°，‎ ‎∴BM＝＝＝a，‎ ‎∴，‎ ‎∴△ABC是“神奇三角形”；‎ ‎②当AC边上的中线与AC边上的高的比为时，‎ 设BM＝a，BC＝2a，‎ ‎∵∠ACB＝90°，‎ ‎∴CM＝＝a，‎ ‎∴AC＝2a，‎ ‎∴AC＝BC，不合题意，舍去；‎ 同理，当BC边上的中线与BC边上的高的比为时，也不符合题意，舍去；‎ 当AB边上的中线与AB边上的高的比为时，‎ 当BC＞AC时，如图，作AB边上的中线CM，作AB边上的高线CD，‎ 设CM＝a，CD＝2a，则DM＝a，‎ ‎∵∠ACB＝90°，‎ ‎∴CM＝AB＝AM，‎ ‎∴AD＝（﹣1）a，‎ ‎∴tanA＝＝，‎ 当BC＜AC时，如图，作AB边上的中线CM，作AB边上的高线CD，‎ 同理可得，tanA＝．‎ 综合可得tanA的值为或．‎ ‎（2）证明：如图，作CH⊥AB于点H，AE⊥BC于点E，AE交CD于K，连接BK，‎ ‎∵AB＝AC，‎ ‎∴E是BC的中点，‎ ‎∵CD是AB边上的中线，‎ ‎∴点K是△ABC的重心，‎ ‎∴KC＝2DK，‎ ‎∵AE是BC的垂直平分线，‎ ‎∴KC＝KB，‎ ‎∴∠KBC＝∠KCB＝45°，‎ ‎∴∠CKB＝90°，‎ 即BK⊥CD，‎ ‎∴＝tan∠CDH＝＝2，‎ ‎∴，‎ ‎∴△ABC是“神奇三角形”．‎ ‎2．解：（1）∠BDP＝∠EPC，‎ 理由如下：∵△ABC为等边三角形，‎ ‎∴∠B＝60°，‎ ‎∵∠DPE＝60°，‎ ‎∴∠DPE＝∠B，‎ ‎∵∠DPC是△BDP的外角，‎ ‎∴∠DPE+∠EPC＝∠B+∠BDP，‎ ‎∴∠EPC＝∠BDP；‎ ‎（2）∵△PDE为正三角形，‎ ‎∴PD＝PE，‎ 在△BDP和△CPE中，‎ ‎，‎ ‎∴△BDP≌△CPE（AAS），‎ ‎∴BD＝CP，BP＝CE，‎ ‎∴BD+CE＝CP+BP＝BC＝8；‎ ‎（3）∵DE∥BC，△ABC为等边三角形，‎ ‎∴△ADE为等边三角形，‎ ‎∴AD＝AE，‎ ‎∴BD＝CE，‎ ‎∵∠B＝∠C，∠EPC＝∠BDP，‎ ‎∴△BDP∽△CPE，‎ ‎∴＝，即＝，‎ 整理得，BD＝，‎ ‎﹣BP2+8BP＝﹣（BP﹣4）2+16，‎ ‎∴BD的最大值为4．‎ ‎3．（1）解：∠ADE＝45°．‎ ‎∵AB＝AC，∠BAC＝90°，‎ ‎∴∠ABC＝∠ACB＝45°，‎ ‎∵∠ACM＝∠ACB，‎ ‎∴∠ACM＝∠ABC，‎ 在△ABD 和△ACE 中，‎ ‎，‎ ‎∴△ABD≌△ACE（SAS），‎ ‎∴AD＝AE，∠CAE＝∠BAD，‎ ‎∴∠DAE＝∠BAC＝90°，‎ ‎∴∠ADE＝45°；‎ ‎（2）（1）中的结论成立 证明：∵∠BAC＝90°，AB＝AC，‎ ‎∴∠B＝∠ACB＝45°．‎ ‎∵∠ACM＝∠ACB，‎ ‎∴∠B＝∠ACM＝45°．‎ 在△ABD 和△ACE 中，‎ ‎，‎ ‎∴△ABD≌△ACE（SAS）．‎ ‎∴AD＝AE，∠BAD＝∠CAE．‎ ‎∴∠CAE+∠DAC＝∠BAD+∠DAC＝∠BAC＝90°．‎ 即∠DAE＝90°．‎ ‎∵AD＝AE，‎ ‎∴∠ADE＝∠AED＝45°．‎ ‎（3）△CGH为等腰直角三角形．理由如下：‎ ‎∵∠BCA＝∠ACE＝45°，‎ ‎∴∠GCH＝90°，‎ 又∵AH⊥BC，AG⊥CE，‎ ‎∴AG＝AH，‎ ‎∵∠ACG＝∠AGC＝45°，‎ ‎∴AG＝CG，‎ ‎∵AB＝AC，AH⊥BC，‎ ‎∴∠HCA＝∠HAC＝45°，‎ ‎∴AH＝HC，‎ ‎∴CH＝CG，‎ ‎∴△CGH为等腰直角三角形．‎ ‎4．（1）发现 解：①∵在△ABC中，AB＝AC，∠BAC＝60°，‎ ‎∴∠BAC＝∠DAE＝60°，‎ ‎∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，即∠BAD＝∠CAE，‎ 在△BAD和△CAE中，‎ ‎，‎ ‎∴△BAD≌△CAE（SAS），‎ ‎∴∠ACE＝∠B＝60°，‎ ‎∴∠DCE＝∠ACE+∠ACB＝60°+60°＝120°；‎ 故答案为：120°，‎ ‎②∵△BAD≌△CAE，‎ ‎∴BD＝CE，‎ ‎∴BC＝BD+CD＝EC+CD，‎ ‎∴CA＝BC＝CE+CD；‎ 故答案为：CA＝CE+CD．‎ ‎（2）探究 ‎∠DCE＝90°；CA＝CD+CE．‎ 理由：∵△ABC和△ADE均为等腰直角三角形，∠BAC＝∠DAE＝90°，‎ ‎∴AB＝AC，AD＝AE，∠BAC﹣∠DAC＝∠DAE﹣∠DAC，‎ 即∠BAD＝∠CAE．‎ ‎∴△BAD≌△CAE（SAS）．‎ ‎∴BD＝CE，∠B＝∠ACE＝45°．‎ ‎∴∠DCE＝∠ACB+∠ACE＝90°．‎ 在等腰直角三角形ABC中，CB＝CA，‎ ‎∵CB＝CD+DB＝CD+CE，‎ ‎∴CA＝CD+CE．‎ ‎（3）应用 DA＝5或．‎ 作DE⊥AB于E，连接AD，‎ ‎∵在Rt△ABC中，AB＝6，AC＝4，∠BAC＝90°，‎ ‎∴BC＝＝＝2，‎ ‎∵∠BDC＝90°，DB＝DC，‎ ‎∴DB＝DC＝，∠BCD＝∠CBD＝45°，‎ ‎∵∠BDC＝∠BAC＝90°，‎ ‎∴点B，C，A，D四点共圆，‎ ‎∴∠DAE＝45°，‎ ‎∴△ADE是等腰直角三角形，‎ ‎∴AE＝DE，‎ ‎∴BE＝6﹣DE，‎ ‎∵BE2+DE2＝BD2，‎ ‎∴DE2+（6﹣DE）2＝26，‎ ‎∴DE＝1，DE＝5，‎ ‎∴AD＝或AD＝5．‎ ‎5．解：（1）∵a＝，（）2＝5，‎ ‎∴a＝﹣5，b＝5，‎ ‎∵A（a，0），B（b，0），‎ ‎∴A（﹣5，0），B（5，0），‎ ‎∴OA＝OB＝5．‎ 如图1，连接OC，设OD＝x，‎ ‎∵C（2，7），‎ ‎∴S△AOC＝×5×7＝17.5，‎ ‎∵S△AOC＝S△AOD+S△COD，‎ ‎∴5x•＝17.5，‎ ‎∴x＝5，‎ ‎∴点D的坐标为（0，5）；‎ ‎（2）如图2，‎ ‎∵A（﹣5，0），B（5，0），C（2，7），‎ ‎∴S△ABC＝×（5+5）×7＝35，‎ ‎∵点P在y轴上，‎ ‎∴设点P的坐标为（0，y），‎ ‎∵S△ACP＝S△ADP+S△CDP，D（0，5），‎ ‎∴5×|5﹣y|×+2×|5﹣y|×＝35，‎ 解得：y＝﹣5或15，‎ ‎∴点P的坐标为（0，﹣5）或（0，15）；‎ ‎（3）7m+3n是定值．‎ ‎∵点Q在x轴的上方，‎ ‎∴分两种情况考虑，‎ 如图3，当点Q在直线BC的左侧时，过点Q作QH⊥x轴，垂足为H，连接CH，‎ ‎∵S△QBC＝S△QHC+S△HBC﹣S△QHB，且S△QBC＝20，‎ ‎∴，‎ ‎∴7m+3n＝﹣5．‎ 如图4，当点Q在直线BC的右侧时，‎ 过点Q作QH⊥x轴，垂足为H，连接CH，‎ ‎∵S△QBC＝S△QHC+S△HBC﹣S△QHB，且S△QBC＝20，‎ ‎∴＝20，‎ ‎∴7m+3n＝75，‎ 综上所述，7m+3n的值为﹣5或75．‎ ‎6．解：（1）∵．‎ ‎∴a﹣2b＝0，b﹣2＝0，‎ 解得a＝4，b＝2，‎ ‎∴A（0，4），C（2，0）；‎ ‎∴x＝＝1，y＝＝2，‎ ‎∴D（1，2）．‎ 故答案为（0，4），（2，0），（1，2）．‎ ‎（2）如图1中，‎ 由条件可知：P点从C点运动到O点时间为2秒，Q点从O点运动到A点时间为2秒，‎ ‎∴0＜t≤2时，点Q在线段AO上，‎ 即 CP＝t，OP＝2﹣t，OQ＝2t，AQ＝4﹣2t，‎ ‎∴S△DOP＝OP•yD＝（2﹣t）×2＝2﹣t，S△DOQ＝OQ•xD＝×2t×1＝t，‎ ‎∵S△ODP＝S△ODQ，‎ ‎∴2﹣t＝t，‎ ‎∴t＝1；‎ ‎（3）的值不变，其值为2．理由如下：如图2中，‎ ‎∵∠2+∠3＝90°，‎ 又∵∠1＝∠2，∠3＝∠FCO，‎ ‎∴∠GOC+∠ACO＝180°，‎ ‎∴OG∥AC，‎ ‎∴∠1＝∠CAO，‎ ‎∴∠OEC＝∠CAO+∠4＝∠1+∠4，‎ 如图，过H点作AC的平行线，交x轴于P，则∠4＝∠PHC，PH∥OG，‎ ‎∴∠PHO＝∠GOF＝∠1+∠2，‎ ‎∴∠OHC＝∠OHP+∠PHC＝∠GOF+∠4＝∠1+∠2+∠4，‎ ‎∴＝，‎ ‎＝，‎ ‎＝2．‎ ‎7．解：（1）∵|a+2|+（b+2a）2＝0，‎ ‎∴a+2＝0，b+2a＝0，‎ 解得a＝﹣2，b＝4，‎ ‎∴A（﹣2，0），B（0，4）；‎ ‎（2）如图1所示，过C作CE⊥OB于E，与PB交于F，‎ ‎∵BC⊥AB，‎ ‎∴∠ABO+∠EBC＝90°，‎ 在Rt△BCE中，∠EBC+∠BCE＝90°，‎ ‎∴∠ABO＝∠BCE，‎ 在△AOB和△BEC中，‎ ‎，‎ ‎∴△AOB≌△BEC（AAS），‎ ‎∴BE＝AO＝2，‎ 又∵OB＝4，‎ ‎∴E为OB的中点，‎ ‎∵EC∥OP，‎ ‎∴EF为△BOP的中位线，则F为BP的中点，‎ 在Rt△BCP中，CF为斜边上的中线，‎ ‎∴CF＝PB＝BF，‎ ‎∴∠BCE＝∠CBD＝∠ABO，‎ 在△AOB和△CDB中 ‎，‎ ‎∴△AOB≌△CDB（AAS），‎ ‎∴CD＝AO＝2；‎ ‎（3）如图2所示，过B作BG⊥CQ于点G，延长QC与x轴交于H，‎ ‎∵∠ABP+∠PBC＝90°，∠PBC+CBQ＝90°，‎ ‎∴∠ABP＝∠CBQ，‎ 在△ABP与△CBQ中，‎ ‎，‎ ‎∴△ABP≌△CBQ（SAS），‎ ‎∴∠BPO＝∠BQG，CQ＝AP＝2+p，‎ 在△BOP和△BGQ中，‎ ‎，‎ ‎∴△BOP≌△BGQ（AAS），‎ ‎∴∠OBP＝∠GBQ，BG＝BO＝4，‎ 又∵∠GBQ+∠PBG＝90°，‎ ‎∴∠OBP+∠PBG＝90°，即∠OBG＝90°，‎ 在四边形OBGH中，∠OBG＝∠BOG＝∠BGH＝90°，‎ ‎∴∠OHG＝90°，‎ ‎∴PH是△PCQ中CQ边上的高，‎ PH＝OH﹣OP＝4﹣p，‎ ‎∴S△PCQ＝•（2+p）（4﹣p）＝﹣+p+4．‎ 故答案为：．‎ ‎8．（1）证明：∵CA＝CB，EB＝ED，∠ABC＝∠DBE＝60°，‎ ‎∴△ABC和△DBE都是等边三角形，‎ ‎∴AB＝BC，DB＝BE，∠A＝60°．‎ ‎∵∠ABC＝∠DBE＝60°，‎ ‎∴∠ABD＝∠CBE，‎ ‎∴△ABD≌△CBE（SAS）．‎ ‎∴∠A＝∠ECB；‎ ‎（2）证明：∵∠ABC＝∠DBE＝45°，CA＝CB，EB＝ED，‎ ‎∴△ABC和△DBE都是等腰直角三角形，‎ ‎∴∠CAB＝45°，‎ ‎∴，‎ ‎∴，‎ ‎∵∠ABC＝∠DBE，‎ ‎∴∠ABD＝∠CBE，‎ ‎∴△ABD∽△CBE，‎ ‎∴∠BAD＝∠BCE＝45°，‎ ‎∵∠ABC＝45°，‎ ‎∴∠ABC＝∠BCE，‎ ‎∴CE∥AB；‎ ‎（3）解：过点D作DM⊥CE于点M，过点D作DN∥AB交CB于点N，‎ ‎∵∠ACB＝90°，∠BCE＝45°，‎ ‎∴∠DCM＝45°，‎ ‎∴∠MDC＝∠DCM＝45°，‎ ‎∴DM＝MC，‎ 设DM＝MC＝a，‎ ‎∴a，‎ ‎∵DN∥AB，‎ ‎∴△DCN为等腰直角三角形，‎ ‎∴DN＝DC＝2a，‎ ‎∵tan∠DEC＝，‎ ‎∴ME＝2DM，‎ ‎∴CE＝a，‎ ‎∴，‎ ‎∵CE∥DN，‎ ‎∴△CEF∽△DNF，‎ ‎∴．‎ ‎9．解：（1）连接PQ，‎ 设经过ts后，P、Q两点的距离为5cm，‎ ts后，PC＝7﹣2tcm，CQ＝5tcm，‎ 根据勾股定理可知PC2+CQ2＝PQ2，‎ 代入数据（7﹣2t）2+（5t）2＝（5）2；‎ 解得t＝1或t＝﹣（不合题意舍去）；‎ ‎（2）设经过ts后，S△PCQ的面积为15cm2‎ ts后，PC＝7﹣2tcm，CQ＝5tcm，‎ S△PCQ＝×PC×CQ＝×（7﹣2t）×5t＝15‎ 解得t1＝2，t2＝1.5，‎ 经过2或1.5s后，S△PCQ的面积为15cm2．‎ ‎（3）设经过ts后，△PCQ的面积最大，‎ ts后，PC＝7﹣2tcm，CQ＝5tcm，‎ S△PCQ＝×PC×CQ＝×（7﹣2t）×5t＝×（﹣2t2+7t）．‎ ‎＝﹣5．‎ ‎∴当t＝s时，△PCQ的面积最大，最大值为cm2．‎ ‎10．解：（1）如图1，AO是BC边上的中线，‎ ‎∵∠ACB＝90°，‎ ‎∴AO2﹣OC2＝AC2，‎ ‎∵AB∇AC＝81，‎ ‎∴AO2﹣OC2＝81，‎ ‎∴AC2＝81，‎ ‎∴AC＝9；‎ ‎（2）①如图2，取BC的中点O，连接AO，‎ ‎∵AB＝AC，‎ ‎∴AO⊥BC，‎ ‎∵∠BAC＝120°，‎ ‎∴∠ABC＝30°，‎ 在Rt△AOB中，‎ ‎∴＝＝6，‎ ‎∴AB∇AC＝AO2﹣BO2＝36﹣108＝﹣72；‎ ‎②如图3，取AC的中点D，连接BD，‎ ‎∴AC＝6，‎ 过点B作BE⊥AC交CA的延长线于点E，‎ ‎∴∠BAE＝180°﹣∠BAC＝60°，‎ ‎∴∠ABE＝30°，‎ ‎∵AB＝12，‎ ‎∴AE＝6，‎ ‎∴BE＝＝＝6．‎ ‎∴DE＝AD+AE＝12，‎ ‎∴＝＝6，‎ ‎∴BA∇BC＝BD2﹣CD2＝＝216；‎ ‎（3）作BD⊥CD，如图4，‎ ‎∵S△ABC＝24，AC＝8，‎ ‎∴＝6，‎ ‎∵AB∇AC＝﹣64，AO是BC边上的中线，‎ ‎∴AO2﹣OC2＝﹣64，‎ ‎∴OC2﹣AO2＝64，‎ 又∵AC2＝82＝64，‎ ‎∴OC2﹣AO2＝AC2，‎ ‎∴∠AOC＝90°，‎ ‎∴OA＝2×＝3，‎ ‎∴＝＝．‎ ‎∴，‎ 在Rt△BCD中，＝＝16，‎ ‎∴AD＝CD﹣AC＝16﹣8，‎ ‎∴＝＝10．‎ ‎11．解：（1）∵△ABC为等边三角形，‎ ‎∴∠B＝∠BAC＝60°，AB＝AC，‎ ‎∵点M是BC的中点，‎ ‎∴∠MAN＝30°，∠AMB＝90°，‎ ‎∵∠AMN＝60°，‎ ‎∴∠BMN＝30°，‎ ‎∴BM＝2BN，AB＝2BM，‎ 设BN＝x，则BM＝2x，AB＝4x，‎ ‎∴AN＝3x，‎ ‎∴；‎ ‎（2）证明：如图2，过点M作MG∥NC交AC于点G，‎ ‎∴∠A＝∠AMG＝∠AGM＝60°，‎ ‎∴△AMG为等边三角形，‎ ‎∴AM＝AG，‎ ‎∴BM＝CG，‎ ‎∵∠AGM＝∠ABC＝60°，‎ ‎∴∠MGC＝∠NBM＝120°，‎ ‎∵MG∥BC，‎ ‎∴∠GMC＝∠MCB，‎ ‎∵∠MNB＝∠MCB，‎ ‎∴∠GMC＝∠MNB，‎ ‎∴△MGC≌△NBM（AAS），‎ ‎∴MG＝BN，‎ ‎∵△AMG为等边三角形，‎ ‎∴AM＝MG，‎ ‎∴AM＝BN；‎ ‎（3）如图3，过点P作PM∥BC交AB于点M，‎ ‎∴△AMP为等边三角形，‎ ‎∴AP＝MP，∠AMP＝60°，‎ ‎∵P为AC的中点，‎ ‎∴AP＝PC，‎ ‎∴MP＝PC，‎ ‎∵∠ACB＝60°，‎ ‎∴∠EMP＝∠PCF＝120°，‎ ‎∵∠AEP＝∠PFC，‎ ‎∴△PCF≌△PME（AAS），‎ ‎∴CF＝ME，‎ ‎∴BF﹣BE＝BC+CF﹣ME+MB，‎ 又∵P为AC的中点，MP∥BC，‎ ‎∴MB＝，‎ ‎∴BF﹣BE＝BC+BC＝，‎ ‎∴．‎ ‎12．解：（1）设运动t秒，M、N两点重合，‎ 根据题意得：2t﹣t＝15，‎ ‎∴t＝15，‎ 答：点M，N运动15秒后，M、N两点重合；‎ ‎（2）如图1，设点M、N运动x秒后，△AMN为等边三角形，‎ ‎∴AN＝AM，‎ 由运动知，AN＝15﹣2x，AM＝x，‎ ‎∴15﹣2x＝x，‎ 解得：x＝5，‎ ‎∴点M、N运动5秒后，△AMN是等边三角形；‎ ‎（3）假设存在，‎ 如图2，设M、N运动y秒后，得到以MN为底边的等腰三角形AMN，‎ ‎∴AM＝AN，‎ ‎∴∠AMN＝∠ANM，‎ ‎∵△ABC是等边三角形，‎ ‎∴AB＝AC，∠C＝∠B＝60°，‎ ‎∴△ACN≌△ABM（AAS），‎ ‎∴CN＝BM，‎ ‎∴CM＝BN，‎ 由运动知，CM＝y﹣15，BN＝15×3﹣2y，‎ ‎∴y﹣15＝15×3﹣2y，‎ ‎∴y＝20，‎ 故点M，N在BC边上运动时，能得到以MN为底边的等腰三角形AMN，此时M，N运动的时间为20秒．‎ ‎13．解：（1）根据正对定义，‎ 当顶角为60°时，等腰三角形底角为60°，‎ 则三角形为等边三角形，‎ 则sad60°＝＝1．‎ 故答案为：1．‎ ‎（2）当∠A接近0°时，sadA接近0，‎ 当∠A接近180°时，等腰三角形的底接近于腰的二倍，故sadA接近2．‎ 于是sadA的取值范围是0＜sadA＜2．‎ 故答案为：0＜sadA＜2．‎ ‎（3）在AB上取点D，使AD＝AC，过点D作DE⊥AC于E，连接CD，如图．‎ ‎∵在Rt△ADE中，＝sin A＝，‎ 设AD＝AC＝5x，则DE＝3x，AE＝4x．‎ ‎∴CE＝x．‎ ‎∴在Rt△CDE中，CD＝＝x．‎ ‎∴sad A＝＝＝．‎ ‎14．解：（1）∵∠ACB＝90°，BC＝4，sin∠ABC＝，‎ ‎∴设AC＝3x，AB＝5x，‎ ‎∴（3x）2+16＝（5x）2，‎ ‎∴x＝1，‎ 即AC＝3，‎ ‎∵BE⊥AD，‎ ‎∴∠AEF＝90°，‎ ‎∵∠AFE＝∠CFB，‎ ‎∴∠DAC＝∠FBC，‎ ‎∴tan∠FBC＝tan∠DAC＝＝；‎ ‎（2）∵AG∥BD，‎ ‎∴∠AGF＝∠CBF，‎ ‎∴tan∠AGF＝tan∠CBF，‎ ‎∴，‎ ‎，‎ ‎∴，‎ ‎∴．‎ ‎∴＝．‎ ‎∵∠EAF＝∠CBF，‎ ‎∴，‎ ‎∴，‎ ‎∴S△DAF＝＝；‎ ‎（3）①当点D在BC的延长线上时，如图1，‎ ‎∵AG＝8，BC＝4，AG∥BD，‎ ‎∴，‎ ‎∴AF＝2CF，‎ ‎∵AC＝3，‎ ‎∴AF＝2，CF＝1，‎ ‎∴，‎ ‎∴，‎ 设AE＝x，GE＝4x，‎ ‎∴x2+16x2＝82，‎ 解得x＝，‎ 即AE＝．‎ 同理tan∠DAC＝tan∠CBF，‎ ‎∴，‎ ‎∴DC＝，‎ ‎∴AD＝＝＝．‎ ‎∴＝．‎ ‎②当点D在BC的边上时，如图2，‎ ‎∵AG∥BD，AG＝8，BC＝4，‎ ‎∴．‎ ‎∴AF＝6，‎ ‎∵∠EAF＝∠CBF＝∠ABC，‎ ‎∴cos∠EAF＝cos∠ABC，‎ ‎∴，‎ ‎∴，‎ 同理，‎ ‎∴，‎ ‎∴．‎ ‎∴DE＝AE﹣AD＝．‎ 综合以上可得DE的长为或．‎ ‎15．解：（1）∵|m﹣3|+（n﹣5）2＝0．‎ ‎∴|m﹣3|＝0，（n﹣5）2＝0．‎ ‎∴m＝3，n＝5，‎ ‎∴B（1，3），C（5，0），‎ ‎∴AB＝3，AC＝4，‎ ‎∴三角形ABC的面积＝；‎ ‎（2）①如图1，当点P在线段AC上时，PC＝t，AP＝4﹣t，‎ 三角形ABP的面积为＝＝6﹣．‎ ‎②如图2，当点P在线段AC的延长线上时，PC＝t，AP＝t﹣4，‎ 三角形ABP的面积为3＝．‎ ‎（3）①当点P在线段AC上时，6﹣．‎ 解得t＝﹣1（舍去）．‎ ‎②如图3，当点P在线段AC的延长线上时，．‎ 解得t＝9．‎ ‎∴OP＝4，PA＝5，‎ ‎∵∠BAC＝90°＝∠DOA，‎ ‎∴OD∥AB，‎ ‎∴．‎ 解得OD＝．‎ ‎∵点D在y轴上且在原点O的上方，‎ ‎∴点D的坐标为（0，）．‎ ‎16．（1）①证明：如图1，‎ ‎∵△ABC和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°．‎ ‎∴AC＝BC，CD＝CE，∠A＝∠ABC＝45°，∠ACB﹣∠DCB＝∠ECD﹣∠DCB，‎ ‎∴∠ACD＝∠BCE，‎ ‎∴△ACD≌△BCE（SAS）．‎ ‎②解：∵△ACD≌△BCE．‎ ‎∴AD＝BE，∠CBE＝∠A＝45°，‎ ‎∴∠DBE＝90°，‎ ‎∴BD2+BE2＝DE2，即BD2+AD2＝DE2，‎ ‎（2）①证明：如图2，‎ ‎∵△ABC和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°．‎ ‎∴由（1）易知△ACD≌△BCE．‎ ‎∴∠DAC＝∠CBE，‎ ‎∴∠ABF+∠BAF＝∠ABC+∠CBE+∠BAF＝∠ABC+∠BAF+∠DAC＝∠ABC+∠BAC＝90°．‎ ‎∴∠AFB＝90°，‎ 即AF⊥BE．‎ ‎②如图3，∵△BDE为等边三角形，DF⊥BE，‎ ‎∴∠DEF＝60°，‎ 设EF＝BF＝a，则DE＝2a，‎ ‎∴a，‎ ‎∵BD＝BE，DC＝CE，‎ ‎∴BC是DE的垂直平分线，‎ ‎∴NE＝a，BN＝a，‎ ‎∴BC＝．‎ ‎∴．‎ 即△DCE与△ABC的边长之比为．‎ ‎17．（1）解：∵B（0，2），‎ ‎∴OB＝2，‎ 在Rt△AOB中，∠BAO＝30°，‎ ‎∴AB＝2OB＝4；‎ ‎（2）证明：，‎ ‎∵AM⊥AB，‎ ‎∴∠BAM＝90°，‎ ‎∴∠MAN＝90°﹣∠BAO＝60°，‎ ‎∵MN垂直平分OA，‎ ‎∴∠ANM＝90°，‎ ‎∴∠AMN＝30°，‎ ‎∴MA＝2AN＝OA，‎ ‎∵△ABC是等边三角形，‎ ‎∴AC＝AB，∠BAC＝60°，‎ ‎∴∠OAC＝90°＝∠MAB，‎ ‎∴△MAB≌△OAC（SAS），‎ ‎∴MB＝OC；‎ ‎（3）解：P是MC的中点．理由如下：‎ 如图2，过点C作CH⊥AB于H，‎ ‎∴∠AHC＝90°＝∠HAM，‎ ‎∵△ABC是等边三角形，‎ ‎∴BC＝AB，∠BCH＝∠ACH＝30°＝∠BAO，‎ ‎∴△BCH≌△BAO（AAS），‎ ‎∴OA＝CH，‎ 由（2）知，AM＝OA，‎ ‎∴AM＝CH，‎ ‎∵∠CPH＝∠MPA，‎ ‎∴△CHP≌△MAP（AAS），‎ ‎∴CP＝MP，‎ 即点P为MC的中点．‎ ‎18．解：（1）∵AB＝BC，‎ ‎∴∠A＝∠BCA＝40°，‎ ‎∴∠ABC＝180°﹣∠A﹣∠BCA＝180°﹣40°﹣40°＝100°‎ 故答案为：100．‎ ‎（2）①在△ABC中，AB＝BC，BD⊥AC，‎ ‎∴AD＝DC，∠ABF＝50°，‎ ‎∵EC＝EF，∠CEF＝80°，点F在BD上，‎ ‎∴∠DFC＝50°，‎ 又∠ADB＝∠CDF＝90°，‎ ‎∴△ABD≌△CFD（AAS），‎ ‎∴BD＝DF，‎ ‎∴BE+EC＝BE+EF＝2BD＝2＝2‎ ‎＝2．‎ ‎②连结AE并延长交BC于M．‎ 若点F在直线BD上，BF是AC的垂直平分线，‎ ‎∵∠AFD＝∠DFC＝50°，又∠ABF＝50°，‎ ‎∴AF∥BC，‎ 若点F在直线BD的左侧，如图2，‎ ‎∵EC＝EF＝AE，‎ ‎∴∠MEF＝2∠EAF，‎ ‎∵∠MEC＝2∠EAD，‎ ‎∴2∠DAF＝∠CEF，‎ ‎∴∠DAF＝40°，∠BCA＝40°．‎ ‎∴AF∥BC．‎ 若点F在直线BD的右侧，如图3．‎ ‎∵EC＝EF＝AE，‎ ‎∴∠MEF＝2∠EAF，‎ ‎∵∠MEC＝2∠EAD，‎ ‎∴2∠DAF＝∠CEF，‎ ‎∴∠DAF＝40°，∠BCA＝40°．‎ ‎∴AF∥BC．‎ ‎19．解：（1）∵2a2+2ab+b2﹣8a+16＝0，‎ ‎∴（a+b）2+（a﹣4）2＝0，‎ ‎∴a+b＝0，a﹣4＝0，‎ 即a＝4，b＝﹣4，‎ 故答案为：4，﹣4；‎ ‎（2）过点P作PM⊥AP交y轴于点M，过P作PN⊥y轴于点N，‎ ‎∵∠OPC＝∠MPA＝∠OAC＝90°，‎ ‎∴∠OPM＝∠APC，∠POM＝∠C，‎ ‎∵∠PAM＝45°，‎ ‎∴PA＝PM，‎ ‎∴△ACP≌△MOP（AAS），‎ ‎∴AC＝MO，‎ 又∵，‎ ‎∴，‎ ‎∴AC＝MO＝1，‎ ‎∴C（1，4）；‎ ‎（3）△BOD的面积不发生变化，理由，‎ ‎∵点A（0，4），B（﹣4，0），‎ ‎∴直线AB的解析式为y＝x+4，‎ ‎①当点P的横坐标大于等于﹣2而小于0时，设D（m，n）如图2，‎ 过点D作DF⊥x轴于F，过点P作PE⊥DF，交FD的延长线于E，‎ ‎∴∠PED＝∠DFO＝90°，OF＝m，DF＝n，‎ ‎∴∠DPE+∠PDE＝90°，‎ ‎∵∠ODP＝90°，‎ ‎∴∠PDE+∠ODF＝90°，‎ ‎∴∠DPE＝∠ODE，‎ ‎∵DP＝OD，‎ ‎∴△PDE≌△DOF（AAS），‎ ‎∴DE＝OF＝m，PE＝DF＝n，‎ ‎∴EF＝DE+DF＝m+n，PE﹣OF＝n﹣m，‎ ‎∴P（m﹣n，m+n），‎ 而点P在线段AB上，‎ ‎∴m+n＝m﹣n+4，‎ ‎∴n＝2，‎ ‎∴点D的纵坐标为2，‎ ‎②当点P的横坐标小于﹣2而大于﹣4时，如图3，‎ 同①的方法得出点D的纵坐标为2，‎ 即：点P从点B向点A运动的过程中，点D的纵坐标始终为2，‎ ‎∴S△BOD＝OB•|yD|＝×4×2＝4，‎ 即：点P从点B向点A运动的过程中，△BOD的面积始终不变，是4．‎ ‎20．解：如图1，过I点分别作IM，IN，IK垂直于AB，BC，AC于点M，N，K，连接IC，‎ ‎∵AI平分∠BAC，IM⊥AB，IK⊥AC，‎ ‎∴IM＝IK，同理IM＝IN，‎ ‎∴IK＝IN，‎ 又∵IK⊥AC，IN⊥BC，‎ ‎∴CI平分∠BCA；‎ ‎（2）如图2，过C点作CE⊥AB于点E，则d的最大值为CE长，‎ ‎∵AC＝5，BC＝12，‎ ‎∴＝，‎ 又∵＝30，‎ ‎∴CE＝，‎ ‎∴d的最大值为．‎ ‎∴小季正确；‎ 假设此时AI平分∠BAC，如图3，连接BI，过I点作IG，IH，IF分别垂直于AC，BC，AB于点G，H，F，‎ ‎∵AI平分∠BAC，CD平分∠ACB，‎ ‎∴BI平分∠CBA，‎ ‎∵IG⊥AC，IH⊥BC，ID⊥AB，‎ ‎∴IG＝IH＝IF＝d，‎ ‎∵S△ACB＝S△AIC+S△BIC+S△ABI，‎ ‎∴，‎ ‎∴＝，‎ ‎∴d＝2，‎ ‎∴假设成立，当d＝2时，连接AI，则AI平分∠BAC，‎ ‎∴小何正确．‎