湖北通山县沙店中学2020-2021学年九年级数学12月检测卷（word版含手写答案） 7页

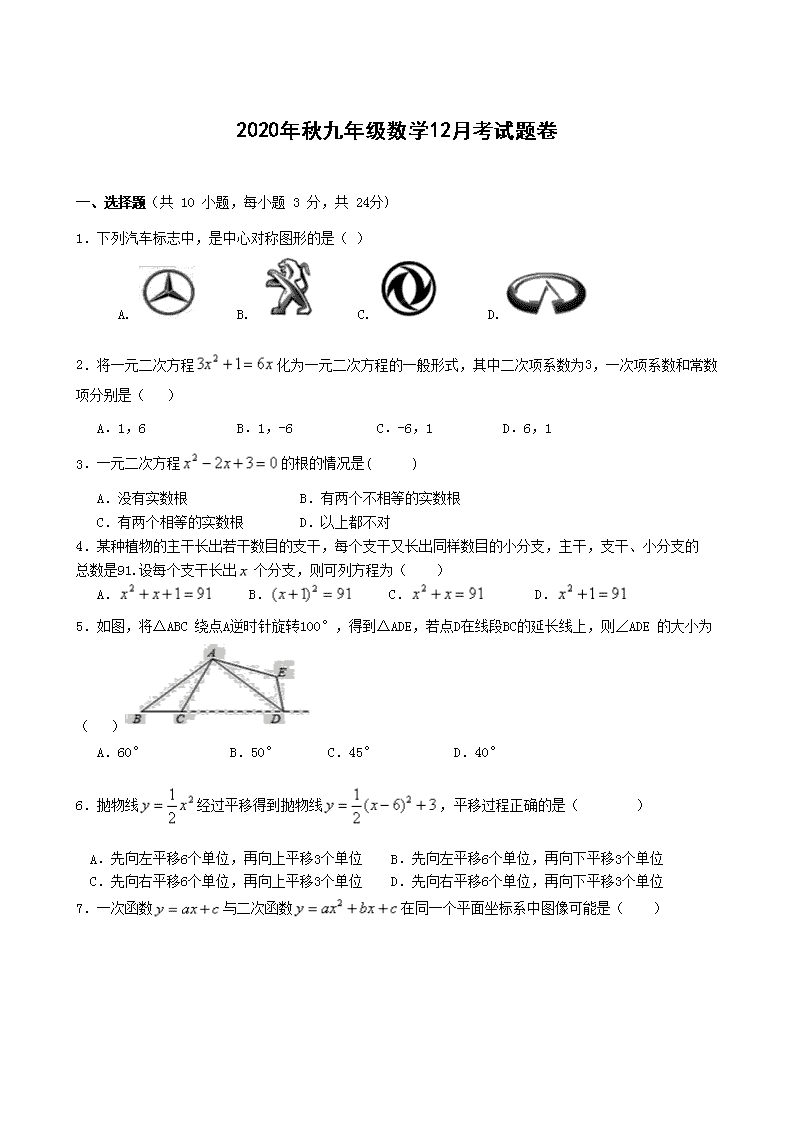
2020年秋九年级数学12月考试题卷 一、选择题（共 10 小题，每小题 3 分，共 24分) 1．下列汽车标志中，是中心对称图形的是（ ） A. B. C. D. 2．将一元二次方程 化为一元二次方程的一般形式，其中二次项系数为3，一次项系数和常数 项分别是（ ） A．1，6 B．1，-6 C．-6，1 D．6，1 3．一元二次方程 的根的情况是( ) A．没有实数根 B．有两个不相等的实数根 C．有两个相等的实数根 D．以上都不对 4．某种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干，支干、小分支的 总数是91.设每个支干长出 个分支，则可列方程为（ ） A． B． C． D． 5．如图，将△ABC 绕点A逆时针旋转100°，得到△ADE，若点D在线段BC的延长线上，则∠ADE 的大小为 （ ） A．60° B．50° C．45° D．40° 6．抛物线 经过平移得到抛物线 ，平移过程正确的是（ ） A．先向左平移6个单位，再向上平移3个单位 B．先向左平移6个单位，再向下平移3个单位 C．先向右平移6个单位，再向上平移3个单位 D．先向右平移6个单位，再向下平移3个单位 7．一次函数 与二次函数 在同一个平面坐标系中图像可能是（ ） A B C D 8．如图是抛物线型拱桥，当拱顶高离水面2m时，水面宽4m。水面上升1.5m，水面宽度为（ ） A．1m B．2m C． m D． m 二、填空题（共8小题，每小题3分，共24分) 9．如果 是方程 的一个根，这个方程的另一个根为 。 10．在平面直角坐标系中，点A(-4,1)关于原点对称的点的坐标是 。 11．已知 、 是一元二次方程 的两个实根，则 。 12．一名男生推铅球，铅球行进的高度 （单位：m）与水平距离 （单位：m）之间的关系是 ，则这个男生这次推铅球的成绩是 。 13．若A（﹣4，y1），B（﹣3，y2），C（1，y3）为二次函数 的图象上的三点，则y1，y2， y3的大小关系是 。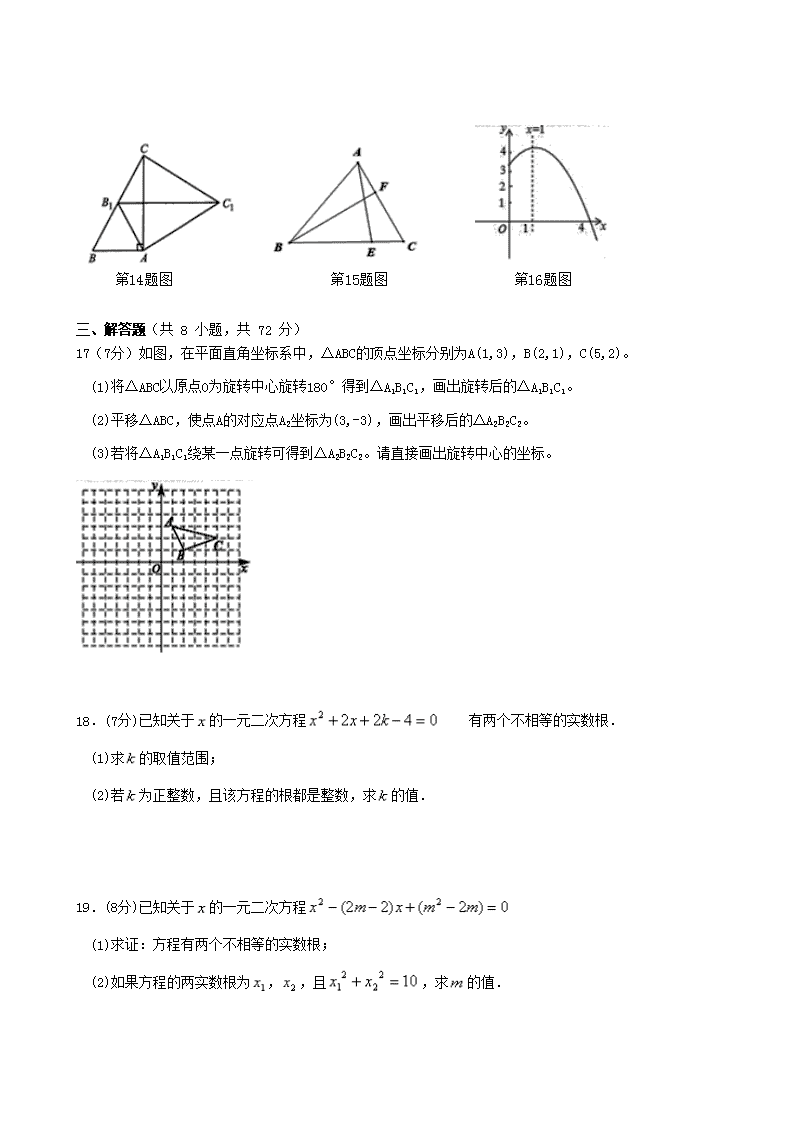 14．如图，在Rt△ABC中，∠BAC=90°，AB=2．将△ABC绕点A按顺时针方向旋转至△AB1C1的位置，点B1恰好 落在边BC的中点处，则CC1的长为________。 15．如图，在△ABC中，∠ABC＝45°，AB＝ ，AC＝8，BC＞6，点E，F分别在BC，AC边上，且AF＝CE， 则AE＋BF=______。 16．抛物线 （ ≠0）的部分图象如图所示，与 轴的一个交点坐标为(4,0)，抛物线的 对称轴是 。下列结论中：① ＞0；② ；③方程 有两个不相等的实数 根；⑤若点 在该抛物线上，则 ≤ 。其中正确的有 。 第14题图 第15题图 第16题图 三、解答题（共 8 小题，共 72 分） 17（7分）如图，在平面直角坐标系中，△ABC的顶点坐标分别为A(1,3)，B(2,1)，C(5,2)。 (1)将△ABC以原点O为旋转中心旋转180°得到△A1B1C1，画出旋转后的△A1B1C1。 (2)平移△ABC，使点A的对应点A2坐标为(3,-3)，画出平移后的△A2B2C2。 (3)若将△A1B1C1绕某一点旋转可得到△A2B2C2。请直接画出旋转中心的坐标。 18．(7分)已知关于 的一元二次方程 有两个不相等的实数根． (1)求 的取值范围； (2)若 为正整数，且该方程的根都是整数，求 的值． 19．(8分)已知关于 的一元二次方程 (1)求证：方程有两个不相等的实数根； (2)如果方程的两实数根为 ， ，且 ，求 的值． 20（9分）如图，抛物线 与 轴交于点 ， 对称轴为直线 ，点D为抛物线的顶点． (1)求抛物线解析式和顶点D的坐标； (2)求抛物线与 轴的两交点A、B的坐标； (3)你可以直接写出不等式 ＜0的解集吗？ 21（9分）如图，点 ， 分别在正方形ABCD的边BC，CD上，且∠MAN=45°，把△ADN绕点A顺时针旋转90° 得到△ABE。 （1）求证：△AEM≌△ANM。 （2）若BM=3，DN=2，求正方形ABCD的边长。 22．（10分）小明投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量 （件）与销 售单价 （元）之间的关系可近似的看作一次函数： ，在销售过程中销售单价不低于成本 价，而每件的利润不高于成本价的60%。 （1）设小明每月获得利润为 （元），求每月获得利润 （元）与销售单价 （元）之间的函数关 系式，并确定自变量 的取值范围？ （2）当销售单价定为多少元时，每月可获得最大利润？每月的最大利润是多少？ （3）如果小明想要每月获得的利润不低于2000元，那么小明每月的成本最少需要多少元？（成本=进 价×销售量） 23．(10分)定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线． （1）如图1，在△ABC中，AB＝AC，AD是△ABC的角平分线，E，F分别是BD，AD上的点． 求证：四边形ABEF是邻余四边形． （2）如图2，在5×4的方格纸中，A，B在格点上，请画出一个符合条件的邻余四边形ABEF，使AB是邻余线， E，F在格点上． （3）如图3，在（1）的条件下,Q为AB（不与A,B重合）上一点，N为AC的中点，连接DQ,NE交于点M,且满足 QB／NC=DB／CE，若DE＝2BE，QB＝3，求邻余线AB的长． 24.(12分)如图，抛物线 与 轴相交于A，B两点，与 轴相交于点C，OA=2，OB=4，直线l 是抛物线的对称轴，在直线l右侧的抛物线上有一动点D，连接AD，BD，BC，CD。 （1）求抛物线的函数表达式； （2）若点D在 轴的下方，当△BCD的面积是 时，求△ABD的面积； （3）在（2）的条件下，点M是 轴上一点，点N是抛物线上一动点，是否存在点N，使得以点B，D，M，N 为顶点，以BD为一边的四边形是平行四边形，若存在，求出点N的坐标；若不存在，请说明理由．