中考数学专题复习练习：锐角三角函数 6页

锐角三角函数 类型1. 锐角三角函数的运算 例1.在△ABC中,∠C=90°，如果tanA＝ ，那么sinB的值等于( )  A. B. C. D.‎ 例2. 计算的值是 .‎ 巩固练习：‎ ‎1. 计算：2sin60°= . ‎ ‎2. 化简＝（ ）‎ A B. C. D. ‎ ‎3.计算：(1) (2) ‎ 类型2. 锐角三角函数的应用 例1. 如图1，王英同学从A地沿北偏西60º方向走‎100m到B地，再从B地向正南方向走‎200m到C地，此时王英同学离A地 （　　）‎ A. m B. ‎100 m C. ‎150m 　　　D. m 例2. 如图2，在高楼前点测得楼顶的仰角为，向高楼前进‎60米到点，又测得仰角为，则该高楼的高度大约为（ ） ‎ 图3 ‎ 图2‎ 图1 ‎ A. ‎82米 B. ‎163米 C. ‎52米 D. ‎‎70米 ‎ ‎ 例3. 一艘轮船自西向东航行，在A处测得东偏北21.3°方向有一座小岛C，继续向东航行‎60海里到达B处，测得小岛C此时在轮船的东偏北63.5°方向上．之后，轮船继续向东航行多少海里，距离小岛C最近？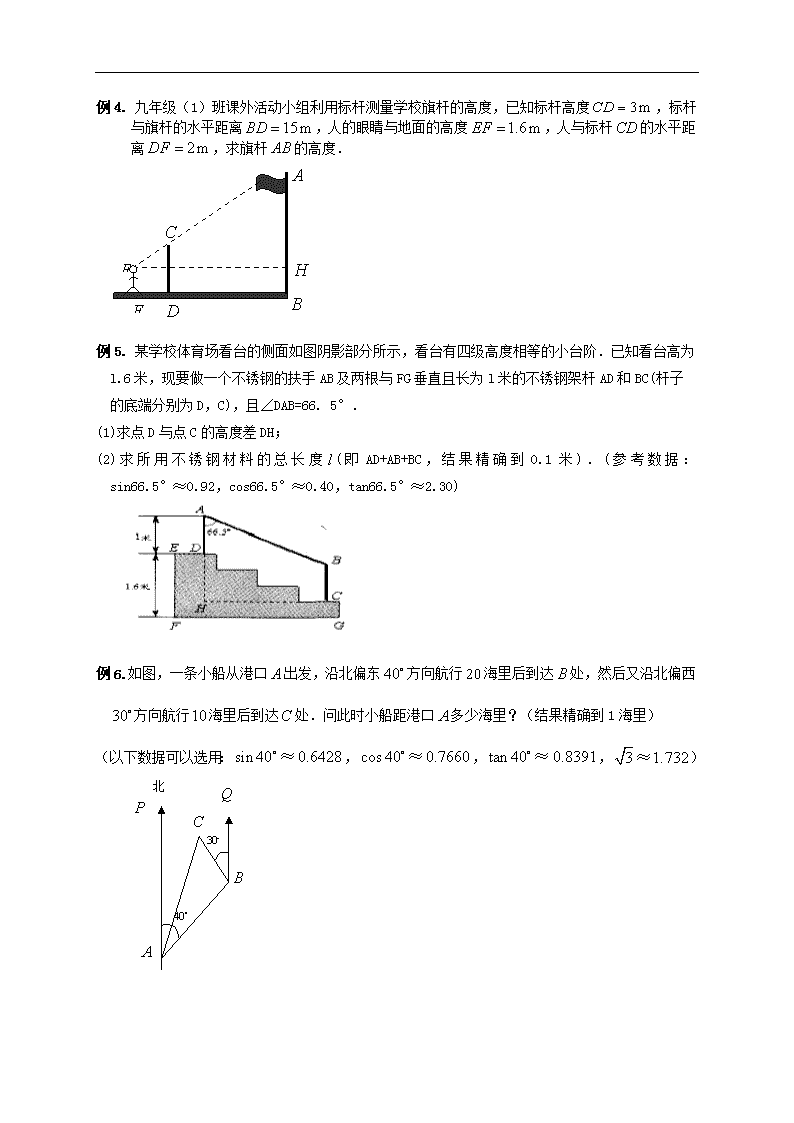（参考数据：sin21.3°≈，tan21.3°≈， sin63.5°≈，tan63.5°≈2）‎ 例4. 九年级（1）班课外活动小组利用标杆测量学校旗杆的高度，已知标杆高度，标杆与旗杆的水平距离，人的眼睛与地面的高度，人与标杆的水平距离，求旗杆的高度．‎ 例5. 某学校体育场看台的侧面如图阴影部分所示，看台有四级高度相等的小台阶．已知看台高为 l‎.6米，现要做一个不锈钢的扶手AB及两根与FG垂直且长为l米的不锈钢架杆AD和BC(杆子 的底端分别为D，C)，且∠DAB=66. 5°．‎ ‎(1)求点D与点C的高度差DH；‎ ‎(2)求所用不锈钢材料的总长度(即AD+AB+BC，结果精确到‎0.1米)．(参考数据：sin66.5°≈0.92，cos66.5°≈0.40，tan66.5°≈2.30)‎ 例6. 如图，一条小船从港口出发，沿北偏东方向航行海里后到达处，然后又沿北偏西方向航行海里后到达处．问此时小船距港口多少海里？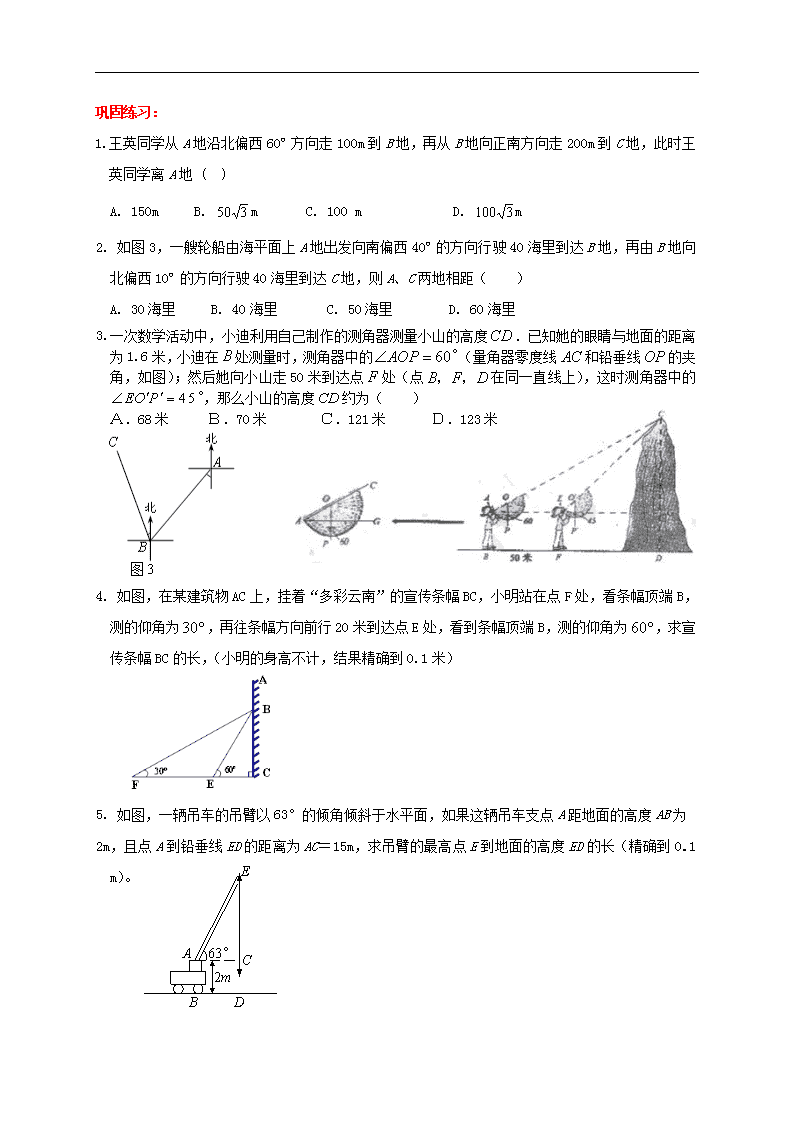（结果精确到‎1海里）‎ ‎（以下数据可以选用：，，，）‎ 巩固练习：‎ ‎1. 王英同学从A地沿北偏西60º方向走‎100m到B地，再从B地向正南方向走‎200m到C地，此时王英同学离A地 ( )‎ A. ‎150m B. m C. ‎100 m D. m ‎ ‎2. 如图3，一艘轮船由海平面上A地出发向南偏西40º的方向行驶‎40海里到达B地，再由B地向北偏西10º的方向行驶‎40海里到达C地，则A、C两地相距（　　） A. ‎30海里 B. ‎40海里 C. ‎50海里 D. 60海里 ‎3. 一次数学活动中，小迪利用自己制作的测角器测量小山的高度．已知她的眼睛与地面的距离为‎1.6米，小迪在处测量时，测角器中的（量角器零度线和铅垂线的夹角，如图）；然后她向小山走‎50米到达点处（点在同一直线上），这时测角器中的，那么小山的高度约为（　　）‎ Ａ．‎68米 Ｂ．‎70米 Ｃ．‎121米 Ｄ．‎‎123米 图3 ‎ ‎4. 如图，在某建筑物AC上，挂着“多彩云南”的宣传条幅BC，小明站在点F处，看条幅顶端B，测的仰角为，再往条幅方向前行‎20米到达点E处，看到条幅顶端B，测的仰角为，求宣传条幅BC的长，（小明的身高不计，结果精确到‎0.1米）‎ ‎63°‎ ‎2m A E C B D ‎5. 如图，一辆吊车的吊臂以63°的倾角倾斜于水平面，如果这辆吊车支点A距地面的高度AB为 ‎2m‎，且点A到铅垂线ED的距离为AC＝‎15m，求吊臂的最高点E到地面的高度ED的长（精确到‎0.1 m）。‎ ‎6.如图，一枚运载火箭从地面处发射，当火箭到达点时，从地面处的雷达站测得的距离是，仰角是．后，火箭到达点，此时测得的距离是，仰角为，解答下列问题：‎ ‎（1）火箭到达点时距离发射点有多远（精确到‎0.01km）？‎ ‎（2）火箭从点到点的平均速度是多少（精确到‎0.1km/s）？ ‎ ‎7. 经过江汉平原的沪蓉(上海—成都)高速铁路即将动工.工程需要测量汉江某一段的宽度.如图①，一测量员在江岸边的A处测得对岸岸边的一根标杆B在它的正北方向，测量员从A点开始沿岸边向正东方向前进‎100米到达点C处，测得. ‎ ‎ （1）求所测之处江的宽度（）；‎ ‎ （2）除(1)的测量方案外，请你再设计一种测量江宽的方案，并在图②中画出图形.‎ A C B 图①‎ 图②‎ 类型3. 综合问题 例1.已知：在△ABC中 ，AD为∠BAC的平分线，以C为圆心，CD为半径的半圆交 ‎ BC的延长线于点E，交AD于点F，交AE于点M，且∠B＝∠CAE，FE:FD＝4:3． ⑴ 求证：AF＝DF； ⑵ 求∠AED的余弦值；‎ ‎⑶ 如果BD＝10，求△ABC的面积． ‎ 例2.已知：如图，△ABC内接于⊙O，点D在OC的延长线上，sinB=，∠CAD=30°．‎ ‎ （1）求证：AD是⊙O的切线；（2）若OD⊥AB，BC=5，求AD的长．‎ 例3. 如图，已知⊙O的直径AB垂直于弦CD于E，连结AD、BD、OC、OD，且OD＝5。‎ ‎（1）若，求CD的长；‎ ‎（2）若 ∠ADO：∠EDO＝4：1，求扇形OAC（阴影部分）的面积（结果保留）。‎ 巩固练习：‎ ‎1. 在图1和图2中，已知OA=OB，AB=24，⊙O的直径为10．‎ ‎ （1）如图1，AB与⊙O相切于点C，试求OA的值；‎ ‎（2）如图2，若AB与⊙O相交于D、E两点，且D、E均为AB的三等分点，试求tanA的值．‎ ‎2.已知在Rt△ABC中，∠C=90°，AD是∠BAC的角平分线，以AB上一点O为圆心，AD为弦 作⊙O．‎ ‎ （1）在图中作出⊙O；（不写作法，保留作图痕迹）‎ ‎ （2）求证：BC为⊙O的切线；‎ ‎ （3）若AC=3，tanB=，求⊙O的半径长．‎ ‎3. 已知：如图：BC是半圆O的直径，D、E是半圆O上两点，，CE的延长线与BD的延长线交于点A，过点E作EF⊥BC于点F，交CD与点G。‎ ‎（1）求证：AE=DE ‎（2）若，,求DG；‎ ‎4. 已知：如图，△ABC内接于⊙O，AD是⊙O的直径，点E、F分别在AB、AC的延长线上，EF交⊙O于点M、N，交AD于点H，H是OD的中点，D是弧MN的中点，EH－HF=2，设∠ACB=a，tana=，EH和HF是方程x2-(k+2)x+4k=0的两个实数根。‎ ‎（1）求EH和HF的长；‎ ‎（2）求BC的长。‎