2020九年级数学上册 第二十四章 圆 垂径定理源于生活同步辅导素材 （新版）新人教版 2页

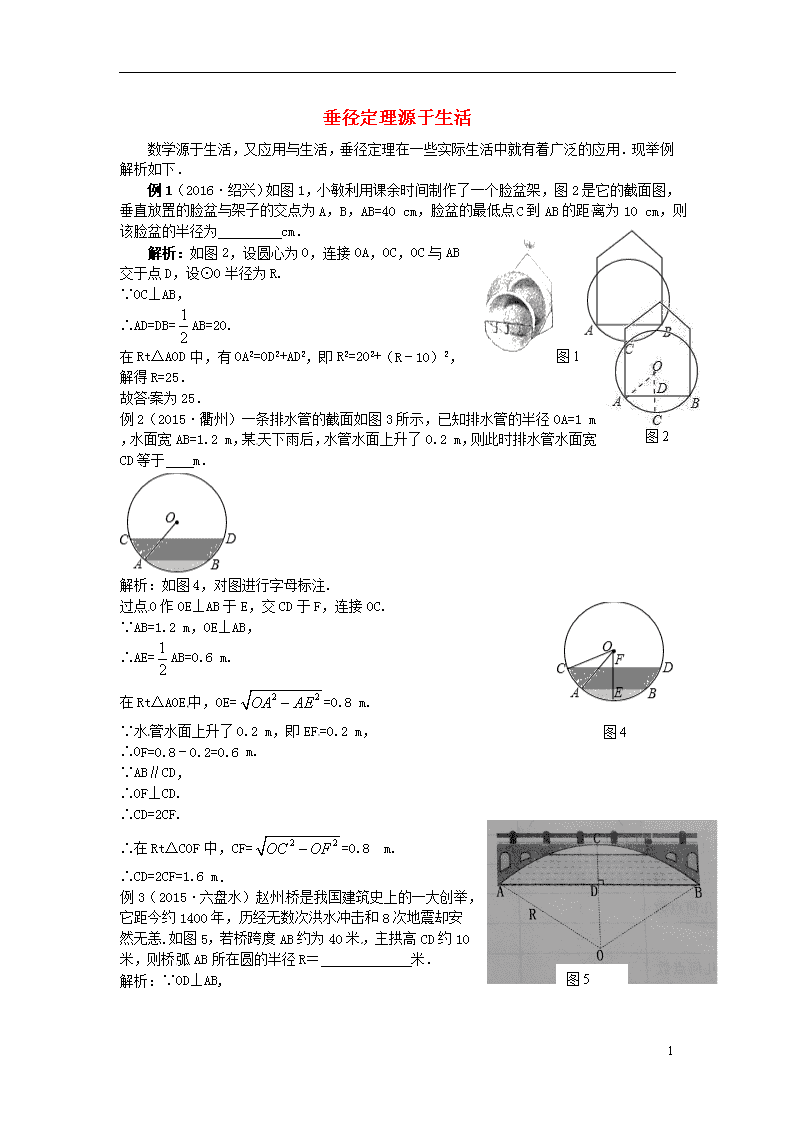
垂径定理源于生活 数学源于生活，又应用与生活，垂径定理在一些实际生活中就有着广泛的应用．现举例解析如下．‎ 图1‎ 例1（2016·绍兴）如图1，小敏利用课余时间制作了一个脸盆架，图2是它的截面图，垂直放置的脸盆与架子的交点为A，B，AB=‎40 cm，脸盆的最低点C到AB的距离为‎10 cm，则该脸盆的半径为　 　cm．‎ 解析：如图2，设圆心为O，连接OA，OC，OC与AB交于点D，设⊙O半径为R.‎ 图2‎ ‎∵OC⊥AB，‎ ‎∴AD=DB=AB=20.‎ 在Rt△AOD中，有OA2=OD2+AD2，即R2=202+（R﹣10）2，‎ 解得R=25．‎ 故答案为25．‎ 例2（2015·衢州）一条排水管的截面如图3所示，已知排水管的半径OA=1 m，水面宽AB=1.2 m，某天下雨后，水管水面上升了0.2 m，则此时排水管水面宽CD等于　　m．‎ 解析：如图4，对图进行字母标注.‎ 图4‎ 过点O作OE⊥AB于E，交CD于F，连接OC.‎ ‎∵AB=‎1.2 m，OE⊥AB，‎ ‎∴AE=AB=‎0.6 m.‎ 在Rt△AOE中，OE==0.8 m.‎ ‎∵水管水面上升了‎0.2 m，即EF=‎0.2 m，‎ ‎∴OF=0.8﹣0.2=‎0.6 m.‎ ‎∵AB∥CD，‎ ‎∴OF⊥CD.‎ 图5‎ ‎∴CD=2CF.‎ ‎∴在Rt△COF中，CF==‎0.8 m.‎ ‎∴CD=2CF=‎1.6 m．‎ 例3（2015·六盘水）赵州桥是我国建筑史上的一大创举，它距今约1400年，历经无数次洪水冲击和8次地震却安然无恙.如图5，若桥跨度AB约为‎40米，主拱高CD约‎10米，则桥弧AB所在圆的半径R＝ 米．‎ 解析：∵OD⊥AB,‎ 2‎ ‎∴AD=AB=20．‎ 在Rt△AOD中，得R2=202+（R﹣10）2，解得R=25（米）．‎ 点评：解决垂径定理的应用问题，常把半弦长、半径、圆心到弦的距离转换到同一直角三角形中，然后通过勾股定理列方程求解，常见辅助线是过圆心作弦的垂线． ‎ 2‎