江西专版2020中考数学复习方案第一单元数与式第03课时整式与因式分解课件 32页

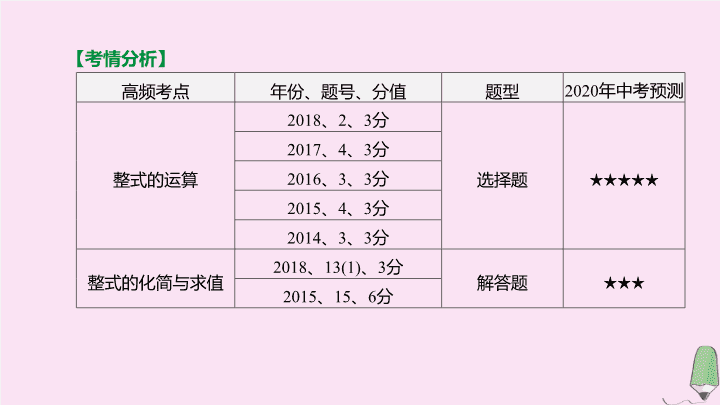
第 3 课时 整式与因式分解 第一单元　数与式 【 考情分析 】 高频考点 年份、题号、分值 题型 2020 年中考预测 整式 的运算 2018 、 2 、 3 分 选择题 ★★★★★ 2017 、 4 、 3 分 2016 、 3 、 3 分 2015 、 4 、 3 分 2014 、 3 、 3 分 整式 的化 简与求值 2018 、 13(1) 、 3 分 解答题 ★★★ 2015 、 15 、 6 分 （续表） 高频考点 年份、题号、分值 题型 2020 年中考预测 因式分解 2019 、 7 、 3 分 填空题 ★★ 2016 、 8 、 3 分 2013 、 7 、 3 分 考点一　整式的概念 内容 单项式 多项式 定义 　 数或字母的 ① 　　　 组成的式子叫做单项式 . 单独的一个数或一个字母也是单项式   　 几个单项式的 ② 　　 叫做多项式   次数 　 一个单项式中 , 所有字母的指数的和叫做这个单项式的次数 　 多项式中 , 次数最高项的次数 , 叫做这个多项式的次数 系数 　 单项式中的数字因数叫做这个单项式的系数 项 　 多项式中 , 每个单项式叫做多项式的项 积 和 考点二　同类项、合并同类项 1 . 同类项 : 所含字母 ③ 　　　　 , 并且相同字母的指数也 ④ 　　　　 的项叫做同类项 . 几个常数项也是同类项 .  2 . 合并同类项 : 合并同类项后 , 所得项的系数是合并前各同类项的系数的和 , 且字母连同它的指数不变 . 相同 相同 【 温馨提示 】 (1) 同类项与系数无关 , 与字母的排列顺序无关 , 如 -7 xy 与 yx 是同类项 . (2) 只有同类项才能合并 , 如 x 2 与 x 3 不能合并 . 考点三　整式的运算 类别 法则 整式的 加减 　 整式的加减实质就是 ⑤ 　　　　　　 . 一般地 , 几个整式相加减 , 如果有括号就先去括号 , 然后再合并同类项   幂的 运算 同底数幂 相乘 a m · a n = ⑥ 　　　　 ( m , n 都是整数 )  幂的 乘方 ( a m ) n = ⑦ 　　　　 ( m , n 都是整数 )  积的 乘方 ( ab ) n = ⑧ 　　　 ( n 为整数 )  同底数幂 相除 a m ÷ a n = ⑨ 　　　　 ( a ≠0, m , n 都为整数 )  合并同类项 a m + n a mn a n b n a m - n ( 续表 ) 类别 法则 整式 的乘法 单项式与单项式相乘 　 把它们的系数、同底数幂分别相乘 , 对于只在一个单项式里含有的字母 , 则连同它的指数作为积的一个因式 单项式与多项式 相乘 m ( a + b + c ) = ⑩ 　　　　　   多项式与多项式 相乘 ( m + n )( a + b ) = ⑪ 　　　 　　   整式 的除法 单项式除以单项式 　 单项式除以单项式 , 把系数与同底数幂分别相除作为商的因式 , 对于只在被除式里含有的字母 , 则连同它的指数作为商的一个因式 多项式除以 单项式 ( am + bm )÷ m=a + b ma + mb + mc ma + mb + na + nb ( 续表 ) 类别 法则 乘法 公式 平方差公式 ( a + b )( a - b ) = ⑫ 　　　   完全平方公式 ( a ± b ) 2 = ⑬ 　　　　　   常用恒 等变形 (1) a 2 + b 2 = ⑭ 　　　　　 = ⑮ 　　　　　 ;  (2)( a - b ) 2 = ⑯ 　　　　 -4 ab  a 2 - b 2 a 2 ±2 ab + b 2 ( a + b ) 2 -2 ab ( a - b ) 2 +2 ab ( a + b ) 2 　 1 . 定义 : 把一个多项式化为几个整式的 ⑰ 　　　　 的形式 , 这样的式子变形叫做这个多项式的因式分解 .  考点四　因式分解 积 2 . 方法 (1) 提公因式法 用字母表示 : ma + mb + mc=m ( a + b + c ) . 公因式的确定 : 取各项系数的最大公约数 , 取各项相同的因式及其最低次幂 . (2) 公式法 3 . 因式分解的一般步骤 一提 ( 提公因式 ), 二套 ( 运用公式 ), 三检查 ( 检查因式分解是否彻底 ) . 考向一　代数式的构建与运用 1 . 某校购进价格为 a 元的排球 100 个 , 价格为 b 元的篮球 50 个 , 则该校一共需支付 ( 　　 ) A . (100 a +50 b ) 元 B . (100 a -50 b ) 元 C . (50 a +100 b ) 元 D . (50 a +100 b ) 元 2 . [2019· 南充 ] 原价为 a 元的书包 , 现按 8 折出售 , 则售价为 　　　　 元 .  A 3 . [2019· 广东 ] 如图 3-1 ①所示的图形是一个轴对称图形 , 且每个角都是直角 , 长度如图①所示 , 小明按如图②所示方法玩拼图游戏 , 两两相扣 , 相互间不留空隙 , 那么小明用 9 个这样的图形 ( 图① ) 拼出来的图形的总长度是 　　　　 . ( 结果用含 a , b 的代数式表示 )  [ 答案 ] a +8 b 　 [ 解析 ] 只有 1 个轴对称图形时长度为 a , 用 2 个轴对称图形时的总长度为 a + b , 用 3 个轴对称图形时的总长度为 a +2 b …… 用 9 个轴对称图形时的总长度为 a +8 b. 图 3-1 考向二　整式的概念及运算 C A A 6 . [2017· 江西 4 题 ] 下列运算正确的是 ( 　　 ) A . (- a 5 ) 2 =a 10 B . 2 a ·3 a 2 = 6 a 2 C . -2 a + a= -3 a D . -6 a 6 ÷2 a 2 = -3 a 3 7 . [2016· 江西 3 题 ] 下列运算正确的是 ( 　　 ) A .a 2 + a 2 =a 4 B . (- b 2 ) 3 = - b 6 C . 2 x ·2 x 2 = 2 x 3 D . ( m - n ) 2 =m 2 - n 2 B 8 . [2014· 江西 3 题 ] 下列运算正确的是 ( 　　 ) A .a 2 + a 3 =a 5 B . (-2 a 2 ) 3 = -6 a 6 C . (2 a +1)(2 a -1) = 2 a 2 -1 D . (2 a 3 - a 2 )÷ a 2 = 2 a -1 D D 10 . [2019· 重庆 A 卷 ] 按如图 3-2 所示的运算程序 , 能使输出 y 值为 1 的是 ( 　　 ) A .m= 1, n= 1 B .m= 1, n= 0 C .m= 1, n= 2 D .m= 2, n= 1 [ 答案 ] D 　 [ 解析 ] 若 m= 1, n= 1, 则 y= 2 m +1 = 3; 若 m= 1, n= 0, 则 y= 2 n -1 = -1; 若 m= 1, n= 2, 则 y= 2 m +1 = 3; 若 m= 2, n= 1, 则 y= 2 n -1 = 1 . 故选 D . 图 3-2 11 . [2019· 绵阳 ] 已知 4 m =a ,8 n =b , 其中 m , n 为正整数 , 则 2 2 m +6 n = ( 　　 ) A .ab 2 B .a + b 2 C .a 2 b 3 D .a 2 + b 3 A 12 . [2019· 无锡 ] 计算 :( a +3) 2 = 　　 　　 .  考向三　整式的化简与求值 a 2 +6 a +9 2 [ 答案 ]11 15 . [2019· 常州 ] 如果 a - b -2 = 0, 那么代数式 1+2 a -2 b 的值是 　　　　 .  5 16 . [2018· 江西 13(1) 题 ] 计算 :( a +1)( a -1)-( a -2) 2 . 解 : 原式 =a 2 -1-( a -2) 2 =a 2 -1-( a 2 -4 a +4) =a 2 -1- a 2 +4 a -4 = 4 a -5 . 18 . 先化简 , 再求值 :( x +3)( x -3)-( x -1) 2 , 其中 x= -2 . 解 : 原式 =x 2 -9-( x 2 -2 x +1) =x 2 -9- x 2 +2 x -1 = 2 x -10 . 当 x= -2 时 , 原式 = -2×2-10 = -14 . 20 . 已知 a + b= 5, ab= 3, 求 : (1) a 2 b + ab 2 的值 ; (2) a 2 + b 2 的值 ; (3)( a 2 - b 2 ) 2 的值 . 解 :(1) 原式 =ab ( a + b ) = 3×5 = 15 . (2) 原式 = ( a + b ) 2 -2 ab = 5 2 -2×3 = 25-6 = 19 . (3) 原式 = ( a - b ) 2 ( a + b ) 2 = 25( a - b ) 2 = 25[( a + b ) 2 -4 ab ] = 25×(25-4×3) = 25×13 = 325 . 21 . [2019· 潍坊 ] 下列因式分解正确的是 ( 　　 ) A . 3 ax 2 -6 ax= 3( ax 2 -2 ax ) B . - x 2 + y 2 = (- x + y )(- x - y ) C .a 2 +2 ab +4 b 2 = ( a +2 b ) 2 D . - ax 2 +2 ax - a= - a ( x -1) 2 考向四　因式分解 D 22 . [2019· 株洲 ] 下列各选项中因式分解正确的是 ( 　　 ) A .x 2 -1 = ( x -1) 2 B .a 3 -2 a 2 + a=a 2 ( a -2) C . -2 y 2 +4 y= 2 y ( y +2) D .m 2 n -2 mn + n=n ( m -1) 2 23 . 若多项式 5 x 2 +17 x -12 可因式分解成 ( x + a )·( bx + c ), 其中 a , b , c 均为整数 , 则 a + c 的值为 ( 　　 ) A . 1 B . 7 C . 11 D . 13 D A 24 . [2019· 江西 7 题 ] 因式分解 : x 2 -1 = 　　　 　 .  25 . [2019· 苏州 ] 因式分解 : x 2 - xy= 　　　　 .  26 . [2019· 温州 ] 分解因式 : m 2 +4 m +4 = 　　　 　 .  27 . [2016· 江西 8 题 ] 分解因式 : ax 2 - ay 2 = 　 　　　 .  (x+1)(x-1) x ( x - y ) ( m +2) 2 a ( x + y )( x - y ) 【 方法点析 】 因式分解就是将一个多项式分解成几个整式的积的形式 . 因式分解的一般步骤 : 先提取公因式 , 再运用公式 , 注意检查每个因式是否能继续分解 . 因式分解常见的错误 :(1) 提公因式只提字母部分 , 系数部分忘记提出 ;(2) 当某项就是公因式时 , 提取后忘记补 1;(3) 因式分解不彻底 , 提公因式后的括号内还能提公因式的忘记再提出 .