2019九年级数学上册 第二十四章圆周角 6页

圆周角 课题：24.1.4 圆周角（1）‎ 课时 ‎ 1 课 时 教学设计 课 标 要 求 ‎ 探索同弧所对的圆周角与圆心角之间的关系，了解并证明圆周角定理及其推论：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半；半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．‎ 教 材 及 学 情 分 ‎ 析 1、 ‎ 教材分析：‎ ‎ 学生在学习本章之前，已通过折叠、对称、平移、旋转、推理证明等方式认识了许多图形的性质，积累了大量的空间与图形的经验．本章是在学习了这些直线型图形的有关性质的基础上，进一步来探索一种特殊的曲线──圆的有关性质．通过本章的学习，对学生今后继续学习数学，尤其是逐步树立分类讨论的数学思想、归纳的数学思想起着良好的铺垫作用．本章的学习是高中的数学学习，尤其是圆锥曲线的学习的基础性工程．‎ 2、 学情分析 ‎ 九年级学生已具备一定知识储备和认知能力。但学生的基础较差，中等、差等生较多，优等生较少。课堂上，多数学生表现欲不强，发言不积极，怕回答错问题；学生应用知识灵活解决问题的能力较差，在几何证明题中，不会抓住已知条件进行论证推理。因此，在教学中，注重学生学习方法的培养，通过学生实践、探究、合作交流来完成本节课的教学。‎ 课 时 教 学 目 标 ‎1．了解圆周角的概念．‎ ‎2．理解圆周角的定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．‎ ‎ 3．理解圆周角定理的推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．‎ ‎4．熟练掌握圆周角的定理及其推理的灵活运用．‎ 重点 ‎ 圆周角的定理、圆周角的定理的推导及运用它们解题 难点 ‎ 运用数学分类思想证明圆周角的定理 教法学法 ‎ 探究法 归纳法 练习法 6‎ 指导 教具 准备 ‎ 课件 教学过程提要 环节 学生要解决的问 题或完成的任务 师生活动 设计意图 引 入 新 课 一、 复习：‎ ‎1、圆心角 ‎2、圆心角、弦、弧之间的关系 一、导入新课 :请同学们口答下面两个问题．‎ ‎ 1．什么叫圆心角？‎ ‎2．圆心角、弦、弧之间有什么内在联系呢？‎ 点评：1．我们把顶点在圆心的角叫圆心角．‎ ‎2．在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对的其余各组量都分别相等。‎ ‎ 巩固上节课所学的内容 6‎ 教 学 过 程 ‎ ‎ 二、探究圆周角定理 ‎1、画图度量：同弧所对的圆周角和圆心角的度数 ‎2、结论:同弧所对的圆周角是圆心角度数的一半 ‎2、证明结论的成立 4、 圆周角定理：‎ 四、用知识解决问题 ‎ 3、导入： 刚才讲的，顶点在圆心上的角，有一组等量的关系，如果顶点不在圆心上，它在其它的位置上？如在圆周上，是否还存在一些等量关系呢？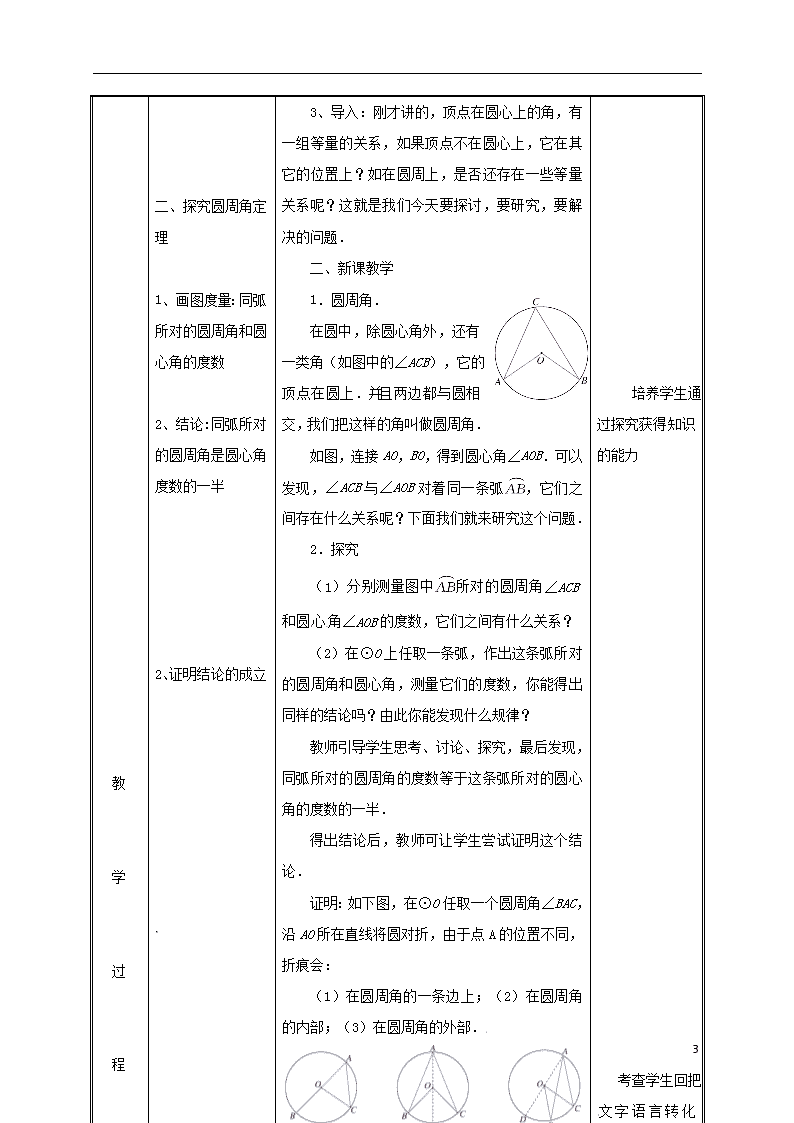这就是我们今天要探讨，要研究，要解决的问题．‎ 二、新课教学 ‎1．圆周角．‎ 在圆中，除圆心角外，还有一类角（如图中的∠ACB），它的顶点在圆上．并且两边都与圆相交，我们把这样的角叫做圆周角．‎ 如图，连接AO，BO，得到圆心角∠AOB．可以发现，∠ACB与∠AOB对着同一条弧，它们之间存在什么关系呢？下面我们就来研究这个问题．‎ ‎2．探究 ‎（1）分别测量图中所对的圆周角∠ACB和圆心角∠AOB的度数，它们之间有什么关系？‎ ‎（2）在⊙O上任取一条弧，作出这条弧所对的圆周角和圆心角，测量它们的度数，你能得出同样的结论吗？由此你能发现什么规律？‎ 教师引导学生思考、讨论、探究，最后发现，同弧所对的圆周角的度数等于这条弧所对的圆心角的度数的一半．‎ 得出结论后，教师可让学生尝试证明这个结论．‎ 证明：如下图，在⊙O任取一个圆周角∠BAC，沿AO所在直线将圆对折，由于点A的位置不同，折痕会：‎ ‎（1）在圆周角的一条边上；（2）在圆周角的内部；（3）在圆周角的外部．‎ 我们来分析第（1）种情况，如图（1），圆心O在∠BAC的一条边上．‎ 对于第（2）（3）种情况，可以通过添加辅助线，如图（2）（3），将它们转化为第（1）种情况，从而得到相同的结论（请你自己证明）．‎ 圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半．‎ 几何语言表示：‎ ‎ ∵ ∠BAC与∠BOC同对弧BC ‎∴ ∠BAC=1/2∠BOC 圆周角定理的推论：同弧或等弧所对的圆周角相等．半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．‎ 几何语言表示：‎ ‎∵AB是直径 ‎∴∠ACB=90度 ‎ ‎ ‎ 培养学生通过探究获得知识的能力 ‎ ‎ ‎ 考查学生回把文字语言转化成文字语言 6‎ 教 学 过 程 五、练习：‎ 三、 讲解例题： ‎ 用所学问题解决问题 ‎ 巩固所学知识 培养学生一题多解的能力 6‎ 小 结 ‎ 1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.‎ ‎ 2.半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是圆的直径 ‎ 3.在同圆(或等圆)中，同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半；相等的圆周角所对的弧相等。‎ ‎ 4.利用圆周角定理解题应注意哪些问题？‎ 板 书 设 计 ‎ 24.1.圆周角 ‎1．圆周角：顶点在圆上，并且两边都与圆相交的角。‎ ‎2．圆周角的定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都相等这条弧所对的圆心角的一半．‎ ‎3．半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径． ‎ 作 业 设 计 绩优学案：p83页 ‎ 1、必做题：1——8题 ‎ 2、选做题：9题 6‎ 教 学 反 思 6‎