圆周角和圆心角的关系(1课时)学案 3页

‎§3.3 圆周角和圆心角的关系（第一课时）‎ 学习目标:‎ ‎　　（1）理解圆周角的概念,掌握圆周角的两个特征、定理的内容及简单应用；‎ ‎　　（2）继续培养学生观察、分析、想象、归纳和逻辑推理的能力；‎ ‎　　（3）渗透由“特殊到一般”，由“一般到特殊”的数学思想方法．‎ 学习重点: 圆周角的概念和圆周角定理 学习难点: 圆周角定理的证明中由“一般到特殊”的数学思想方法和完全归纳法的数学思想．‎ 学习方法:指导探索法.‎ 学习过程:‎ 一、举例：‎ ‎1、已知⊙O中的弦AB长等于半径，求弦AB所对的圆周角和圆心角的度数．‎ ‎2、如图，OA、OB、OC都是圆O的半径，∠AOB=2∠BOC．求证：∠ACB=2∠BAC ‎3、如图，已知圆心角∠AOB=100°，求圆周角∠ACB、∠ADB的度数？‎ ‎4、一条弦分圆为1：4两部分，求这弦所对的圆周角的度数？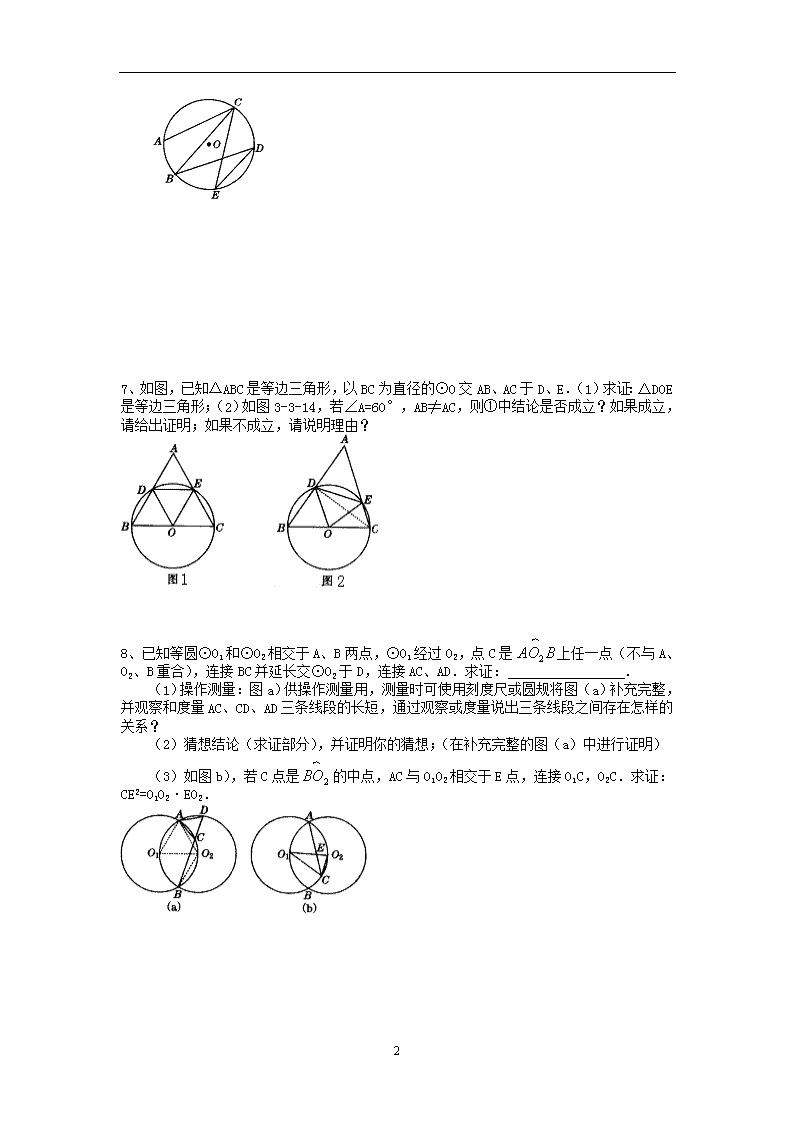‎ ‎5、已知AB为⊙O的直径，AC和AD为弦，AB=2，AC=，AD=1，求∠CAD的度数．‎ ‎6、如图，A、B、C、D、E是⊙O上的五个点，则图中共有 个圆周角，分别是 ．‎ 3‎ ‎7、如图，已知△ABC是等边三角形，以BC为直径的⊙O交AB、AC于D、E．（1）求证：△DOE是等边三角形；（2）如图3-3-14，若∠A=60°，AB≠AC，则①中结论是否成立？如果成立，请给出证明；如果不成立，请说明理由？‎ ‎8、已知等圆⊙O1和⊙O2相交于A、B两点，⊙O1经过O2，点C是上任一点（不与A、O2、B重合），连接BC并延长交⊙O2于D，连接AC、AD．求证： ．‎ ‎（1）操作测量：图a）供操作测量用，测量时可使用刻度尺或圆规将图（a）补充完整，并观察和度量AC、CD、AD三条线段的长短，通过观察或度量说出三条线段之间存在怎样的关系？‎ ‎（2）猜想结论（求证部分），并证明你的猜想；（在补充完整的图（a）中进行证明）‎ ‎（3）如图b），若C点是的中点，AC与O1O2相交于E点，连接O1C，O2C．求证：CE2=O1O2·EO2．‎ 3‎ 二、课外练习：‎ ‎1、⊙O的弦AB等于半径，那么弦AB所对的圆周角一定是（ ）．‎ ‎　　（A）30°　（B）150°　（C）30°或150°　（D）)60°‎ ‎　　2、△ABC中，∠B＝90°，以BC为直径作圆交AC于E，若BC=12，AB=12 ，则 的度数为（ ）．‎ ‎　　（A）60°　（B）80°　（C）100°　（D）)120°‎ ‎　　3、如图，△ABC是⊙O的内接等边三角形，D是AB上一点，AB与CD交于E点，则图中60°的角共有( )个．‎ ‎　　（A）3　（B）4　（C）5　（D）6‎ ‎　　‎ ‎4、如图，△ABC内接于⊙O，∠OBC=25°，则∠A的度数为（ ）‎ ‎　　（A）70°　（B）65°　（C）60°　（D）)50°‎ ‎　　‎ ‎5、圆内接三角形三个内角所对的弧长为3:4:5，那么这个三角形内角的度数分别为__________．‎ ‎　‎ ‎　6、如图，AB是⊙O的直径，CD⊥AB于D，AD=9cm，DB=4cm，求CD和AC的长．‎ ‎7、已知：如图，△ABC是⊙O的内接三角形，⊙O的直径BD交AC于E，AF⊥BD于F，延长AF交BC于G．求证：‎ 3‎