2020年中考三轮冲刺复习培优同步练习：《四边形》（解析版） 50页

三轮冲刺复习培优同步练习：《四边形》‎ ‎1．在平面直角坐标系中，O为原点，点A（，0），点B（0，1），点E是边AB中点，把△ABO绕点A顺时针旋转，得△ADC，点O，B旋转后的对应点分别为D，C．记旋转角为α．‎ ‎（Ⅰ）如图①，当点D恰好在AB上时，求点D的坐标；‎ ‎（Ⅱ）如图②，若α＝60°时，求证：四边形OECD是平行四边形；‎ ‎（Ⅲ）连接OC，在旋转的过程中，求△OEC面积的最大值（直接写出结果即可）．‎ ‎2．如图，在长方形ABCD中，AB＝4cm，BE＝5cm，点E是AD边上的一点，AE、DE分别长acm、bcm，满足（a﹣3）2+|2a+b﹣9|＝0．动点P从B点出发，以2cm/s的速度沿B→C→D运动，最终到达点D．设运动时间为ts．‎ ‎（1）a＝　 　cm，b＝　 　cm；‎ ‎（2）t为何值时，EP把四边形BCDE的周长平分？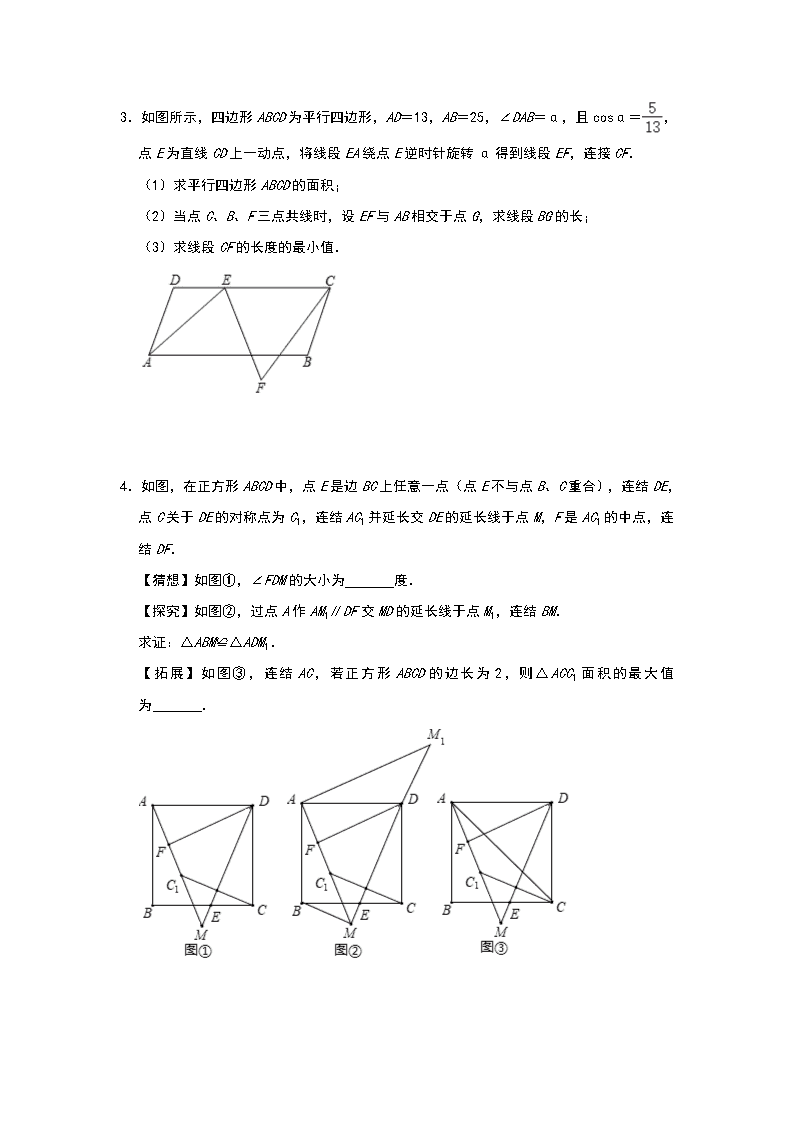‎ ‎（3）另有一点Q从点E出发，按照E→D→C的路径运动，且速度为1cm/s，若P、Q两点同时出发，当其中一点到达终点时，另一点随之停止运动．求t为何值时，△BPQ的面积等于6cm2．‎ ‎3．如图所示，四边形ABCD为平行四边形，AD＝13，AB＝25，∠DAB＝α，且cosα＝，点E为直线CD上一动点，将线段EA绕点E逆时针旋转α得到线段EF，连接CF．‎ ‎（1）求平行四边形ABCD的面积；‎ ‎（2）当点C、B、F三点共线时，设EF与AB相交于点G，求线段BG的长；‎ ‎（3）求线段CF的长度的最小值．‎ ‎4．如图，在正方形ABCD中，点E是边BC上任意一点（点E不与点B、C重合），连结DE，点C关于DE的对称点为C1，连结AC1并延长交DE的延长线于点M，F是AC1的中点，连结DF．‎ ‎【猜想】如图①，∠FDM的大小为　 　度．‎ ‎【探究】如图②，过点A作AM1∥DF交MD的延长线于点M1，连结BM．‎ 求证：△ABM≌△ADM1．‎ ‎【拓展】如图③，连结AC，若正方形ABCD的边长为2，则△ACC1面积的最大值为　 　．‎ ‎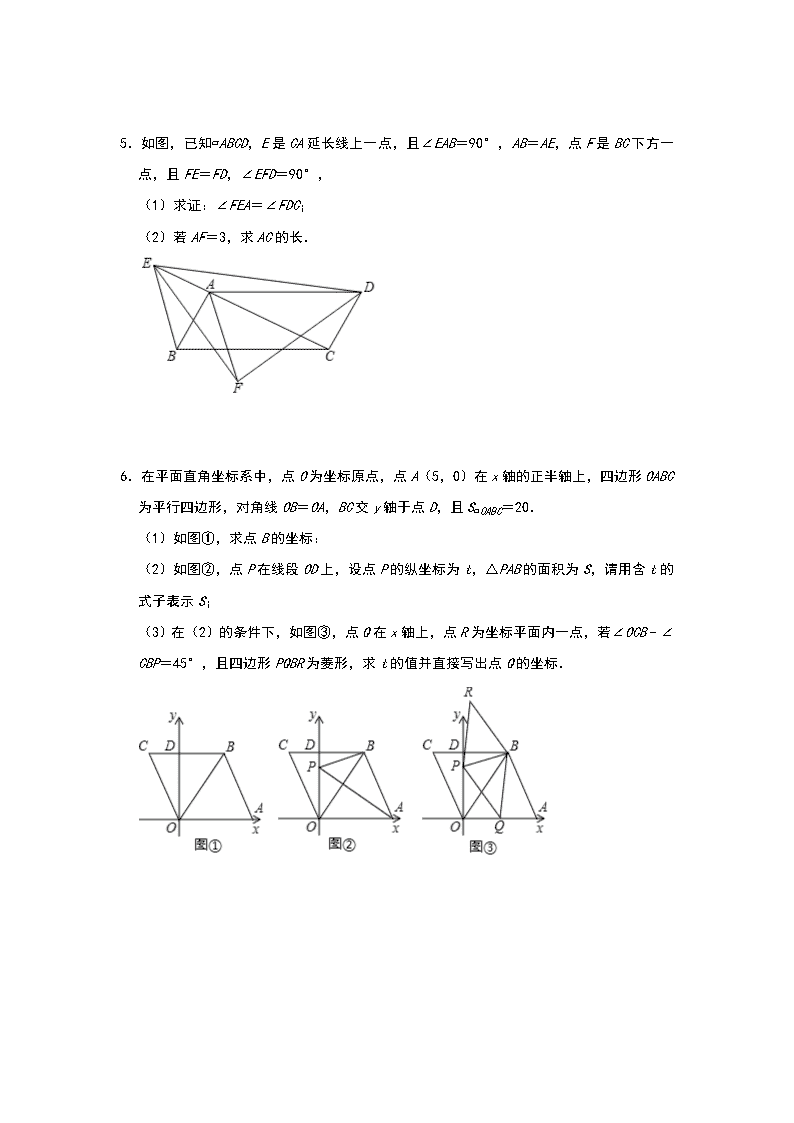5．如图，已知▱ABCD，E是CA延长线上一点，且∠EAB＝90°，AB＝AE，点F是BC下方一点，且FE＝FD，∠EFD＝90°，‎ ‎（1）求证：∠FEA＝∠FDC；‎ ‎（2）若AF＝3，求AC的长．‎ ‎6．在平面直角坐标系中，点O为坐标原点，点A（5，0）在x轴的正半轴上，四边形OABC为平行四边形，对角线OB＝OA，BC交y轴于点D，且S▱OABC＝20．‎ ‎（1）如图①，求点B的坐标：‎ ‎（2）如图②，点P在线段OD上，设点P的纵坐标为t，△PAB的面积为S，请用含t的式子表示S；‎ ‎（3）在（2）的条件下，如图③，点Q在x轴上，点R为坐标平面内一点，若∠OCB﹣∠CBP＝45°，且四边形PQBR为菱形，求t的值并直接写出点Q的坐标．‎ ‎7．已知在四边形ABCD中，AD∥BC，AB⊥BC，AD＝2，AB＝4，BC＝6．‎ ‎（1）如图1，P为AB边上一点，以PD，PC为边作平行四边形PCQD，过点Q作QH⊥BC，交BC的延长线于H．求证：△ADP≌△HCQ；‎ ‎（2）若P为AB边上任意一点，延长PD到E，使DE＝PD，再以PE，PC为边作平行四边形PCQE．请问对角线PQ的长是否存在最小值？如果存在，请求出最小值；如果不存在，请说明理由．‎ ‎（3）如图2，若P为DC边上任意一点，延长PA到E，使AE＝nPA（n为常数），以PE，PB为边作平行四边形PBQE．请探究对角线PQ的长是否也存在最小值？如果存在，请求出最小值；如果不存在，请说明理由．‎ ‎8．如图①，在平行四边形ABCD中，AB＝8，BC＝6，∠ABC＝60°．AE平分∠BAD交CD于点F．动点P从点A出发沿AD向点D以每秒1个单位长度的速度运动．过点P作PQ⊥AD，交射线AE于点Q，以AP、AQ为邻边作平行四边形APMQ，平行四边形APMQ与△ADF重叠部分面积为S．当点P与点D重合时停止运动，设P点运动时间为t秒．（t＞0）‎ ‎（1）用含t的代数式表示QF的长．‎ ‎（2）当点M落到CD边上时，求t的值．‎ ‎（3）求S与t之间的函数关系式．‎ ‎（4）连结对角线AM与PQ交于点G，对角线AC与BD交于点O（如图②）．直接写出当GO与△ABD的边平行时t的值．‎ ‎9．如图①，正方形ABCD的边长为2，点P是正方形ABCD内一点，连结PA，PB，PD，△PAB为等边三角形．‎ ‎（1）求点P到边AD，AB的距离之和；‎ ‎（2）如图②，连结BD交PA于点E，求△PBD的面积以及的值．‎ ‎10．如图，已知∠MON＝90°，A，B分别是边OM和ON上的点，四边形ACDB和四边形OEFC都是正方形．‎ ‎（1）当OA＝2，OB＝1时，求OC的长．‎ ‎（2）当OB＝1，点A在直线OM上运动时，求OC的最小值．‎ ‎（3）设S△CDF＝y，OA＝x，求y关于x的函数关系式．‎ ‎11．已知：如图①，在Rt△ABC中，∠ACB＝90°，BC＝8，AB＝10，点P，E，F分别是AB，AC，BC上的动点，且AP＝2CE＝2BF，连结PE，PF，以PE，PF为邻边作平行四边形PFQE．‎ ‎（1）当点P是AB的中点时，试求线段PF的长．‎ ‎（2）在运动过程中，设CE＝m，若平行四边形PFQE的面积恰好被线段BC或射线AC分成1：3的两部分，试求m的值．‎ ‎（3）如图②，设直找FQ与直线AC交于点N，在运动过程中，以点Q，N，E为顶点的三角形能否构成直角三角形？若能，请直接写出符合要求的CE的长；若不能，请说明理由．‎ ‎12．定义：有三条边相等的四边形称为三等边四边形．‎ ‎（1）如图①，平行四边形ABCD中，对角线CA平分BCD．将线段CD绕点C旋转一个角度α（0°＜α＜∠B）至CE，连结AE．‎ ‎①求证：四边形ABCE是三等边四边形；‎ ‎②如图②，连结BE，DE．求证：∠BED＝∠ACB．‎ ‎（2）如图③，在（1）的条件下，设BE与AC交于点G，∠ABE＝3∠EBC，AB＝10，cos∠BAC＝，求以BG，GE和DE为边的三角形的面积．‎ ‎13．如图，长方形ABCD在平面直角坐标系中，AD∥BC∥x轴，AB∥DC∥y轴，x轴与y轴夹角为90°，点M，N分别在xy轴上，点A（1，8），B（1，6），C（7，6），D（7，8）．‎ ‎（1）连接线段OB、OD、BD，求△OBD的面积；‎ ‎（2）若长方形ABCD在第一象限内以每秒0.5个单位长度的速度向下平移，经过多少秒时，△OBD的面积与长方形ABCD的面积相等请直接写出答案；‎ ‎（3）见备用图，连接 OB，OD，OD交BC于点E，∠BON的平分线和∠BEO的平分线交于点F．‎ ‎①当∠BEO的度数为n，∠BON的度数为m时，求∠OFE的度数．‎ ‎②请直接写出∠OFE和∠BOE之间的数量关系．‎ ‎14．将一个矩形纸片OABC放置在平面直角坐标系中，点O（0，0），点A（8，0），点C（0，6）．P是边OC上的﹣一点（点P不与点O，C重合），沿着AP折叠该纸片，得点O的对应点O'．‎ ‎（Ⅰ）如图①，当点O'落在边BC上时，求点O'的坐标；‎ ‎（Ⅱ）若点O'落在边BC的上方，O'P，O'A与分别与边BC交于点D，E．‎ ‎①如图②，当∠OAP＝30°时，求点D的坐标；‎ ‎②当CD＝O'D时，求点D的坐标（直接写出结果即可）．‎ ‎15．在等腰梯形ABCD中，AD∥BC，AB＝DC＝5，AD＝6，BC＝12．‎ ‎（1）梯形ABCD的面积等于　 　．‎ ‎（2）如图1，动点P从D点出发沿DC以每秒1个单位的速度向终点C运动，动点Q从C点出发沿CB以每秒2个单位的速度向B点运动．两点同时出发，当P点到达C点时，Q点随之停止运动．当PQ∥AB时，P点离开D点多少时间？‎ ‎（3）如图2，点K是线段AD上的点，M、N为边BC上的点，BM＝CN＝5，连接AN、DM，分别交BK、CK于点E、F，记△ADG和△BKC重叠部分的面积为S，求S的最大值．‎ ‎16．【探索规律】‎ 如图①，在△ABC中，点D，E，F分别在AB，BC，AC上，且DF∥BC，EF∥AB．设△ADF 的边DF上的高为h1，△EFC的边CE上的高为h2．‎ ‎（1）若△ADF、△EFC的面积分别为3，1，则＝　 　；‎ ‎（2）设△ADF、△EFC、四边形BDFE的面积分别为S1，S2，S，求证：S＝2；‎ ‎【解决问题】‎ ‎（3）如图②，在△ABC中，点D，E分别在AB，AC上，点F，G在BC上，且DE∥BC，DF∥BG．若△ADE、△DBF、△EGC的面积分别为3，7，5，求△ABC的面积．‎ ‎17．已知：如图，在四边形ABCD中，AB∥CD，∠ABC＝90°，AB＝AD＝10cm，CD＝4cm．点P从点A出发，沿AB方向匀速运动，速度为2cm/s；同时点Q从点C出发，沿DC方向在DC的延长线上匀速运动，速度为1cm/s；当点P到达点B时，点Q停止运动．过点P作PE∥BD，交AD于点E．连接EQ，BQ．设运动时间为t（s）（0＜t＜5），解答下列问题：‎ ‎（1）连接PQ，当t为何值时，PQ∥AD？‎ ‎（2）设四边形PBQE的面积为y（cm2），求y与t的函数关系式；‎ ‎（3）在运动过程中，是否存在某一时刻t，使四边形PBQE的面积为四边形ABQD面积的，若存在，求出t的值；若不存在，请说明理由；‎ ‎（4）在运动过程中，是否存在某一时刻t，使EQ⊥BD？若存在，求出t的值；若不存在，请说明理由．‎ ‎18．已知菱形ABCD中，AB＝4，∠BAD＝120°，点P是直线AB上任意一点，连接PC，在∠PCD内部作射线CQ与对角线BD交于点Q（与B、D不重合），且∠PCQ＝30°．‎ ‎（1）如图，当点P在边AB上，且BP＝3时，求PC的长；‎ ‎（2）当点P在射线BA上，且BP＝n（0≤n＜8）时，求QC的长；（用含n的式子表示）‎ ‎（3）连接PQ，直线PQ与直线BC相交于点E，如果△QCE与△BCP相似，请直接写出线段BP的长．‎ ‎19．如图，在Rt△ABC中，∠ACB＝90°，AC＝12，AB＝20．点P从点B出发，以每秒5个单位长度的速度沿BC向终点C运动，同时点M从点A出发，以相同速度沿AB向终点B运动．过点P作PQ⊥AB于点Q，连结PQ，以PQ、MQ为邻边作矩形PQMN，当点P运动到终点时，整个运动停止，设矩形PQMN与△ABC重叠部分图形的面积为S（S＞0），点P的运动时间为l秒．‎ ‎（1）①BC的长为　 　；‎ ‎②用含l的代数式表示线段PQ的长为　 　．‎ ‎（2）当QM的长度为10时，求t的值；‎ ‎（3）求S与t的函数关系式；‎ ‎（4）当过点Q和点N的直线垂直于Rt△ABC的一边时，直接写出t的值．‎ ‎20．在正方形ABCD中，E，F分别在AD，DC上，且AE＝DF，AF交BD于G．‎ ‎（1）如图1，求证：BE⊥AF．‎ ‎（2）如图2，在边AB上取一点K，使AK＝AE．过K作KS∥AF交BD于S，求证：G是SD中点．‎ ‎（3）在（2）的条件下，如果AB＝8，BE是∠ABD的平分线，求△BSK的面积．‎ 参考答案 ‎1．解：（Ⅰ）∵A（，0），点B（0，1），‎ ‎∴OA＝，OB＝1，‎ 在△AOB中，∠AOB＝90°，tan∠BAO＝＝，‎ ‎∴∠BAO＝30°．‎ ‎∴AB＝2OB＝2，‎ 由旋转性质得，DA＝OA＝，‎ 过D作DM⊥OA于M，如图①所示：‎ 则在Rt△DAM中，DM＝AD＝，AM＝DM＝，‎ ‎∴OM＝AO﹣OM＝﹣，‎ ‎∴D（﹣，）．‎ ‎（Ⅱ）延长OE交AC于F，如图②所示：‎ 在Rt△AOB 中，点E为AB的中点，∠BAO＝30°，‎ ‎∴OE＝BE＝AE．‎ 又∠ABO＝60°，‎ ‎∴△BOE是等边三角形，‎ ‎∴OE＝OB，‎ ‎∴∠BOE＝60°，‎ ‎∴∠EOA＝30°，‎ 由旋转性质，DC＝OB，‎ ‎∴OE＝DC．‎ ‎∵α＝60°，‎ ‎∴∠OAD＝60°，‎ 由旋转性质知，∠DAC＝∠OAB＝30°，∠DCA＝∠OBA＝60°，‎ ‎∴∠OAC＝∠OAD+∠DAC＝90°，‎ ‎∴∠OFA＝90°﹣∠EOA＝90°﹣30°＝60°，‎ ‎∴∠DCA＝∠OFA，‎ ‎∴OE∥DC．‎ ‎∴四边形OECD是平行四边形．‎ ‎（III）由旋转的性质得：在旋转的过程中，点C在以点A为圆心，以AB为半径的圆上，如图③所示：‎ 过点A作AG⊥OE交OE的延长线于G，‎ 当G、A、C三点共线时，△OEC面积最大，‎ ‎∵点E是边AB中点，∠AOB＝90°，AB＝2，‎ ‎∴OE＝BE＝AE＝AB＝1＝OB，‎ ‎∴△OBE是等边三角形，‎ ‎∴∠OEB＝60°，‎ ‎∴∠AEG＝∠OEB＝60°，‎ 在Rt△AEG中，∠AGE＝90°，AE＝1，sin∠AEG＝，‎ ‎∴AG＝AE×isn∠AEG＝1×＝，‎ ‎∴CG＝AG+AC＝AG+AB＝+2，‎ ‎∴△OEC面积的最大值＝OE×CG＝×1×（+2）＝+1．‎ ‎2．解：（1）∵（a﹣3）2+|2a+b﹣9|＝0，‎ ‎∴a﹣3＝0，2a+b﹣9＝0，‎ ‎∴a＝3，b＝3；‎ 故答案为：3，3；‎ ‎（2）∵AE＝3cm，DE＝3cm，‎ ‎∴AD＝6cm＝BC，‎ ‎∴C四边形BCDE＝BC+CD+DE+EB＝18cm，‎ ‎∵EP把四边形BCDE的周长平分，‎ ‎∴BE+BP＝9cm，‎ ‎∴点P在BC上，BP＝4cm，‎ ‎∴t＝＝2s；‎ ‎（3）解：①点P在BC上（0＜t≤3），‎ ‎∵S△BPQ＝×2t×4＝6，‎ ‎∴t＝；‎ ‎②相遇前，点P在CD上（3＜t≤），‎ ‎∵S△BPQ＝×[（4﹣（t﹣3）﹣（2t﹣6）]×6＝6，‎ ‎∴t＝；‎ ‎③相遇后，点P在CD上（＜t≤5），‎ ‎∵S△BPQ＝×[（（t﹣3）+（2t﹣6）﹣4]×6＝6，‎ ‎∴t＝5；‎ ‎∴综上所述，当t＝s或s或5s时，△BPQ的面积等于6cm2．‎ ‎3．解（1）如图1，作DK⊥AB于点K，‎ ‎∵将线段EA绕点E逆时针旋转α得到线段EF，‎ ‎∴∠AEF＝α，AE＝EF，‎ 在Rt△DAK中，‎ ‎∵cos∠DAK＝cosα＝，且AD＝13，‎ ‎∴AK＝5，‎ ‎∴DK＝＝＝12，‎ ‎∴S平行四边形ABCD＝AB×DK＝25×12＝300；‎ ‎（2）如图2，延长CD至H，作∠AHD＝α，‎ ‎∵∠AHD＝∠ADH＝α，‎ ‎∴AH＝AD＝13，‎ 过点A作AM⊥DH于点M，‎ 由（1）知AM＝12，‎ ‎∴DM＝＝5，‎ ‎∴DH＝10，‎ ‎∵∠FEH＝∠DEA+∠α＝∠F+α，‎ ‎∴∠DEA＝∠F，‎ 在△AEH和△EFC中，‎ ‎，‎ ‎∴△AEH≌△EFC（AAS），‎ ‎∴EH＝CF，CE＝AH＝13，‎ ‎∴DE＝CD﹣CE＝12，BF＝CF﹣BC＝22﹣13＝9，‎ ‎∵BG∥CE，‎ ‎∴△FBG∽△FCE，‎ ‎∴，‎ 即，‎ ‎∴BG＝；‎ ‎（3）如图3，延长CD至P，使∠P＝∠ADP＝α，过点F作FM∥BC，交CD于点M，过点FN⊥CD，交CD于点N，‎ 由（2）可知∠AEP＝∠EFM，‎ 在△EAP和△FEM中．‎ ‎，‎ ‎∴△EAP≌△FEM（AAS），‎ ‎∴EM＝AP＝13，FM＝EP，‎ 设DE＝x，则FM＝EP＝10+x，CM＝25﹣（13+x）＝12﹣x，‎ ‎∴FN＝FM•sinα＝（10+x），MN＝FM•cosα＝（10+x），‎ ‎∴CN＝CM+MN＝12﹣x+（10+x）＝，‎ 在Rt△CFN中，CF2＝CN2+NF2＝（208x2﹣416x+56836），‎ 对称轴x＝﹣＝1，‎ ‎∴当x＝1时，CF的值最小，CF的最小值为．‎ ‎4．解：（1）由对称得：CD＝C'D，∠CDE＝∠C'DE，‎ 在正方形ABCD中，AD＝CD，∠ADC＝90°，‎ ‎∴AD＝C'D，‎ ‎∵F是AC'的中点，‎ ‎∴DF⊥AC'，∠ADF＝∠C'DF，‎ ‎∴∠FDM＝∠FDC'+∠EDC'＝∠ADC＝45°；‎ 故答案为：45；‎ ‎（2）∵DF⊥AC1，‎ ‎∴∠DFM＝90°，‎ ‎∵AM1∥DF ‎∴∠MAM'＝90°，‎ 在正方形ABCD中，DA＝BA，∠BAD＝90°，‎ ‎∴∠DAM1＝∠BAM，‎ 由（1）可知：∠FDM＝45°‎ ‎∵∠DFM＝90°‎ ‎∴∠AMD＝45°，‎ ‎∴∠M1＝45°，‎ ‎∴AM＝AM1，‎ 在：△ABM和△ADM1中，‎ ‎∵，‎ ‎∴△ABM≌△ADM1（SAS）；‎ ‎（3）如图，过C1作C1G⊥AC于G，则＝AC•C1G，‎ 在Rt△ABC中，AB＝BC＝2，‎ ‎∴AC＝＝2，即AC为定值，‎ 当C1G最大值，△AC1C的面积最大，‎ 连接BD交AC于O，当C1在BD上时，C1G最大，此时G与O重合，‎ ‎∵CD＝C1D＝2，OD＝AC＝，‎ ‎∴C'G＝C1D﹣OD＝2﹣，‎ ‎∴＝AC•C1G＝×2（2﹣）＝2﹣，‎ 故答案为：2﹣．‎ ‎5．（1）证明：设AC与DF交于点O，如图1所示：‎ ‎∵∠EAB＝90°，‎ ‎∴∠BAC＝90°，‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴AB＝CD，AB∥CD，‎ ‎∴∠ACD＝∠BAC＝90°，‎ ‎∴∠FDC+∠COD＝90°，‎ ‎∵∠EFD＝90°，‎ ‎∴∠FEA+∠FOE＝90°，‎ 又∵∠FOE＝∠COD，‎ ‎∴∠FEA＝∠FDC；‎ ‎（2）解：连接CF，如图2所示：‎ ‎∵AB＝AE，AB＝CD，‎ ‎∴AE＝CD，‎ 在△AEF和△CDF中，，‎ ‎∴△AEF≌△CDF（SAS），‎ ‎∴AF＝CF，∠AFE＝∠CFD，‎ ‎∴∠AFC＝∠EFD＝90°，‎ ‎∴△ACF是等腰直角三角形，‎ ‎∴AC＝AF＝3．‎ ‎6．解：（1）∵点A（5，0），OB＝OA，‎ ‎∴OA＝OB＝5，‎ ‎∵S▱OABC＝OA×OD＝5OD＝20，‎ ‎∴OD＝4，‎ ‎∵四边形OABC为平行四边形，‎ ‎∴BC∥AO，BC＝AO＝5，‎ ‎∴∠BDO＝90°，‎ ‎∴DB＝＝＝3，‎ ‎∴点B（3，4）；‎ ‎（2）∵点P的纵坐标为t，‎ ‎∴OP＝t，‎ ‎∴DP＝4﹣t，‎ ‎∴S＝×（3+5）×4﹣×3×（4﹣t）﹣×5×t＝﹣t+10；‎ ‎（3）如图，‎ 由（1）知，B（3，4），OA＝5，BC∥OA，‎ ‎∴C（﹣2，4），‎ ‎∴CD＝2‎ 取OD的中点E，则DE＝OD＝2，‎ ‎∴DE＝CD，‎ ‎∴∠DCE＝45°，‎ ‎∴∠OCB﹣∠OCE＝45°，‎ ‎∵∠OCB﹣∠CBP＝45°，‎ ‎∴∠OCE＝∠CBP，‎ 过点E作EF⊥OC于F，‎ ‎∴∠CFE＝90°＝∠BDP，‎ ‎∴△CFE∽△BDP，‎ ‎∴，‎ 在Rt△CDE中，CD＝DE＝2，‎ ‎∴CE＝2，‎ 在Rt△ODC中，CD＝2，OD＝4，‎ ‎∴OC＝2，‎ ‎∵CE是△OCD的中线，‎ ‎∴S△OCE＝S△CDO＝××2×4＝2‎ ‎∵S△OCE＝OC•EF＝×EF＝2，‎ ‎∴EF＝，‎ 在Rt△CFE中，根据勾股定理得，CF＝，‎ ‎∴，‎ ‎∴DP＝1，‎ ‎∴OP＝OD﹣DP＝3，‎ ‎∴t＝3，‎ ‎∴P（0，3），‎ 设Q（m，0），‎ ‎∵B（3，4），‎ ‎∴PQ2＝m2+9，BQ2＝（m﹣3）2+16，‎ ‎∵四边形PQBR为菱形，‎ ‎∴PQ＝BQ，‎ ‎∴m2+9＝（m﹣3）2+16，‎ ‎∴m＝，‎ 即Q（，0）．‎ ‎7．解：（1）∵AD∥BC，‎ ‎∴∠ADC＝∠DCH，‎ ‎∴∠ADP+∠PDC＝∠DCQ+∠QCH，‎ ‎∵四边形PCQD是平行四边形，‎ ‎∴PD∥CQ，PD＝CQ，‎ ‎∴∠PDC＝∠DCQ，‎ ‎∴∠ADP＝∠QCH，‎ 在△ADP和△HCQ中，‎ ‎，‎ ‎∴△ADP≌△HCQ（AAS）；‎ ‎（2）存在最小值，最小值为10，‎ 如图1，作QH⊥BC，交BC的延长线于H，设PQ与DC相交于点G，‎ ‎∵PE∥CQ，‎ ‎∴△DPG∽△CQG，‎ ‎∴ ＝ ＝ ，‎ 由（1）可知，∠ADP＝∠QCH，‎ ‎∴Rt△ADP∽Rt△QCH，‎ ‎∴ ＝ ＝ ，‎ ‎∴CH＝2AD＝4，‎ ‎∴BH＝BC+CH＝6+4＝10，‎ ‎∴当PQ⊥AB时，PQ的长最小，即为10；‎ ‎（3）存在最小值，最小值为（ n+4 ），‎ 如图2，作QH∥DC，交CB的延长线于H，作CK⊥CD，交QH的延长线于K，‎ ‎∵PE∥BQ，AE＝nPA，‎ ‎∴＝＝，‎ ‎∵AD∥BC，‎ ‎∴∠ADP+∠DCH＝90°，‎ ‎∵CD∥QK，‎ ‎∴∠QHC+∠DCH＝180°，‎ ‎∴∠QHC＝∠ADQ，‎ ‎∵∠PAD+∠PAG＝∠QBH+∠QBG＝90°，∠PAG＝∠QBG，‎ ‎∴∠PAD＝∠QBH，‎ ‎∴△ADP∽△BHQ，‎ ‎∴＝＝，‎ ‎∴BH＝2n+2，‎ ‎∴CH＝BC+BH＝6+2n+2＝2n+8，‎ 过点D作DM⊥BC于M，又∠DAB＝∠ABM＝90°，‎ ‎∴四边形ABMD是矩形，‎ ‎∴BM＝AD＝2，DM＝AB＝4，‎ ‎∴MC＝BC﹣BM＝6﹣2＝4＝DM，‎ ‎∴∠DCM＝45°，‎ ‎∴∠HCK＝45°，‎ ‎∴CK＝CH•cos45°＝ （ 2n+8 ）＝（ n+4 ），‎ ‎∴当PQ⊥CD时，PQ的长最小，最小值为（ n+4 ）．‎ ‎8．解：（1）如图1中，‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴AD∥BC，∠D＝∠ABC，AD＝BC＝6，‎ ‎∵∠ABC＝60°，‎ ‎∴∠DAB＝120°，∠D＝60°，‎ ‎∵AE平分∠DAB，‎ ‎∴∠DAQ＝60°，‎ ‎∴△ADF是等边三角形，‎ ‎∴AF＝AD＝6，‎ ‎∵PQ⊥AD，‎ ‎∴∠APQ＝90°，‎ ‎∴AQ＝2AP＝2t，‎ ‎∴FQ＝AF﹣AQ＝6﹣2t；‎ ‎（2）如图2中，‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴AB∥CD，‎ ‎∴∠D＝180°﹣∠DAB＝60°，‎ ‎∵PM∥AE，MQ∥AD，‎ ‎∴∠DPM＝∠DAQ＝60°，四边形APMQ是平行四边形，‎ ‎∴△DPM是等边三角形，PM＝AQ＝2PA＝2t，‎ ‎∴DP＝PM，‎ ‎∴6﹣t＝2t，‎ ‎∴t＝2．‎ ‎（3）①当0＜t≤2时，如图1中，重叠部分是平行四边形APMQ，S＝AP•PQ＝t2．‎ ‎②如图3中，当2＜t≤3时，重叠部分五边形APSTQ，‎ S＝t2﹣（3t﹣6）2＝﹣t2+9t﹣9；‎ ‎③如图4中，当3＜t≤6时，重叠部分是四边形PSFA．‎ S＝S△DAF﹣S△DSP＝×62﹣•（6﹣t）2＝﹣t2+3t．‎ 综上所述，S＝；‎ ‎（4）如图5中，当GO∥AB时，∵AG＝GM，‎ ‎∴点M在线段CD上，此时t＝2s．‎ 如图6中，当GO∥AD时，则B、C、Q共线，‎ 可得△ABQ是等边三角形，AB＝AQ＝BQ＝8，‎ ‎∴AQ＝2t＝8，‎ ‎∴t＝4s，‎ 综上所述，t＝2s或4s时，GH与三角形ABD的一边平行或共线．‎ ‎9．解：（1）如图①，过P作PM⊥AD于M，PN⊥AB于N，‎ ‎∵四边形ABCD是正方形，‎ ‎∴∠DAB＝90°，‎ ‎∴∠PMA＝∠DAB＝∠PNB＝90°，‎ ‎∴四边形ANPM是矩形，‎ ‎∴PM＝AN，AM＝PN，‎ ‎∵△ABP是等边三角形，‎ ‎∴AN＝AB＝1，PN＝，‎ ‎∴PM＝AN＝1，‎ ‎∴PM+PN＝+1，‎ 即点P到边AD，AB的距离之和为+1；‎ ‎（2）S△PBD＝S四边形ABPD﹣S△ABD＝AD（PM+PN）﹣AD•AB＝×2×（1+）﹣×2×2＝﹣1；‎ 如图②，过P作PG⊥BD于G，过A作AH⊥BD于H，‎ ‎∴∠PGE＝∠AHE＝90°，‎ ‎∵∠PEG＝∠AEH，‎ ‎∴△PGE∽△AHE，‎ ‎∴＝，‎ ‎∵＝＝＝＝+1，‎ ‎∴＝+1．‎ ‎10．解：（1）如图1所示，过点C作CG⊥OM于点G，‎ ‎∵四边形ACDB是正方形，‎ ‎∴AB＝AC，∠BAC＝90°，‎ ‎∵∠MON＝90°，∠AGC＝90°，‎ ‎∴∠BAO+∠ABO＝90°，∠BAO+∠CAG＝90°，‎ ‎∴∠ABO＝∠CAG，‎ ‎∴△AOB≌△AGC（AAS）．‎ ‎∵OA＝2，OB＝1，‎ ‎∴CG＝OA＝2，AG＝OB＝1，‎ ‎∴OG＝3，‎ ‎∴在Rt△OGC中，由勾股定理得：‎ OC＝＝．‎ ‎（2）如图2所示，由题意可得点C在直线l：y＝x﹣1上运动，‎ ‎∴OC的最小值为当OC与直线l垂直时，此时OC＝，‎ ‎∴OC的最小值为．‎ ‎（3）如图3所示，延长OC至点H，使CH＝OC，连接AH，过点C作CG⊥OM，‎ ‎∵CD＝CA，CH＝CF，∠DCF＝∠ACH＝90°+∠ACF，‎ ‎∴△DCF≌△ACH（SAS），‎ 由（1）知△AOB≌△AGC（AAS），‎ ‎∴CG＝OA，‎ ‎∵C是OH的中点，‎ ‎∴S△ACH＝S△OAC，‎ ‎∵S△CDF＝y，OA＝x，‎ ‎∴y＝S△OAH ‎＝S△OAC ‎＝x2．‎ ‎∴y关于x的函数关系式为y＝x2．‎ ‎11．解：（1）如图①，作PH⊥BC于点H，‎ ‎∵∠ACB＝90°，BC＝8，AB＝10，‎ ‎∴AC＝6．‎ ‎∵AP＝2CE＝2BF，‎ ‎∵点P是AB的中点，‎ ‎∴PA＝PB＝5．‎ ‎∴CE＝BF＝，PH＝3，BH＝CH＝4，‎ ‎∴FH＝．‎ ‎∴PF＝＝．‎ ‎（2）如图②，平行四边形PFQE的面积恰好被线段BC分成1：3的两部分时，则EM＝PF．‎ ‎∵PH⊥BC，‎ ‎∴∠PHF＝90°＝∠ACB，‎ ‎∴PH∥AC，‎ ‎∴△CEM∽△HPF，△PBH∽△ABC，‎ ‎∴PH＝2CE＝2m，＝．‎ ‎∴＝，‎ ‎∴m＝．‎ 如图③，平行四边形PFQE的面积恰好被线段AC分成1：3的两部分时，则FD＝QD，QN＝PG，‎ ‎∴CF＝PG．‎ ‎∵△APG∽△ABC，‎ ‎∴＝．‎ ‎∴＝，‎ ‎∴m＝．‎ ‎∴m的值为或．‎ ‎（3）如图④，当∠QNE＝90°时，则点N与点C重合，设CE＝x，‎ ‎∵△PBH∽△ABC，‎ ‎∴＝，‎ ‎∴＝，‎ ‎∴x＝．‎ 如图⑤，当∠QNE＝90°时，则点P与点B重合，‎ 则2x＝10，‎ ‎∴x＝5．‎ 如图⑥，当∠QNE＝90°时，‎ ‎∵△FPR∽△PES，‎ ‎∴＝，‎ ‎∴＝，‎ ‎∴x＝．‎ 经检验，x值符合题意．‎ 综上，CE的长为或5或．‎ ‎12．解：（1）①证明：如图①，‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴AB∥CD，‎ ‎∴∠BAC＝∠ACD，‎ ‎∵CA平分∠BCD，‎ ‎∴∠BCA＝∠ACD，‎ ‎∴∠BAC＝∠BCA，‎ ‎∴AB＝BC，‎ ‎∴平行四边形ABCD是菱形，‎ ‎∴AB＝BC＝CD，‎ ‎∵CE＝CD，‎ ‎∴AB＝BC＝CE，‎ ‎∴四边形ABCE是三等边四边形．‎ ‎②证明：如图②，延长EC至点H，‎ ‎∵CE＝CD，‎ ‎∴∠CDE＝∠CED，‎ ‎∴∠HCD＝∠CDE+∠CED＝2∠CED，‎ ‎∵BC＝CE，‎ ‎∴∠CBE＝∠CEB，‎ ‎∴∠HCB＝∠CBE+∠CEB＝2∠CEB，‎ ‎∴∠HCD﹣∠HCB＝2（∠CED﹣∠CEB），‎ 即∠BCD＝2∠BED，‎ ‎∵四边形ABCD是菱形，‎ ‎∴∠BCD＝2∠ACB，‎ ‎∴∠BED＝∠ACB．‎ ‎（2）如图③，连接BD，DG，BD与AC交于点O，过点G作GP⊥BC于点P，‎ ‎∵四边形ABCD是菱形，‎ ‎∴BD⊥AC，AO＝AC，BD＝2BO，∠DBC＝∠ABC，‎ 在Rt△ABO中，AB＝10，cos∠BAC＝，‎ ‎∴AO＝AB＝6，‎ ‎∴OC＝AO＝6，BO＝＝8，‎ ‎∴BD＝2BO＝16，‎ ‎∵∠ABE＝3∠EBC，‎ ‎∴∠ABC＝4∠EBC，‎ ‎∵∠DBC＝∠ABC，‎ ‎∴∠DBC＝2∠EBC，‎ ‎∴∠DBE＝∠EBC，‎ ‎∵GO⊥BD，GP⊥BC，‎ ‎∴GO＝GP，BP＝BO＝8，‎ ‎∴PC＝BC﹣BP＝10﹣8＝2，‎ 在Rt△GPC中，GC2﹣GP2＝PC2，‎ ‎∴（OC﹣OG）2﹣OG2＝PC2，‎ 即（6﹣OG）2﹣OG2＝4，‎ ‎∴OG＝，GC＝，‎ ‎∴BG＝＝，‎ ‎∵∠BED＝∠ACB，∠DBE＝∠EBC，‎ ‎∴△BED∽△BCG，‎ ‎∴，‎ ‎∴BE＝＝16×10÷＝6，‎ DE＝＝16×＝2，‎ ‎∵AC垂直平分BD，‎ ‎∴DG＝BG＝，‎ ‎∴∠GDB＝∠GBD，‎ ‎∴∠GDE＝∠BDE﹣∠GDB＝∠BGC﹣∠GBD＝∠GOB＝90°，‎ ‎∴S△GDE＝DG•DE＝＝，‎ ‎∴以BG，GE和DE为边的三角形的面积是．‎ ‎13．解：（1）如图1，延长DA交y轴于H，如图1所示：‎ 则AH⊥y轴．‎ ‎∵A（1，8），B（1，6），C（7，6），D（7，8）‎ ‎∴OH＝8，DH＝7，AH＝1，AD＝6，AB＝2，‎ ‎∴S△OBD＝S△ODH﹣S△ABD﹣S梯形AHOB＝×OH×DH﹣×AB×AD﹣×（AB+OH）×AH＝×8×7﹣×2×6﹣×（2+8）×1＝17；‎ ‎（2）∵S长方形ABCD＝2×6＝12，‎ ‎∴S△OBD＝S△ODH﹣S△ABD﹣S梯形AHOB＝12，‎ ‎∴×（8﹣0.5t）×7﹣×2×6﹣×（2+8﹣0.5t）×1＝12，‎ ‎∴t＝；‎ ‎（3）①如图2，延长CB交y轴于P，延长EF交y轴于点G，‎ ‎∵EF平分∠BEO，OF平分∠NOB，‎ ‎∴∠GOF＝∠NOB＝m，∠BEF＝∠BEO＝n，‎ ‎∵∠EFO＝∠GOF+∠FGO，∠FGO＝∠GPE+∠BEF，‎ ‎∴∠EFO＝∠GOF+∠GPE+∠BEF＝m+n+90°；‎ ‎②∵EF平分∠BEO，OF平分∠NOB，‎ ‎∴∠GOF＝∠NOB，∠BEF＝∠BEO，‎ ‎∵∠EFO＝∠GOF+∠FGO，∠FGO＝∠GPE+∠BEF，‎ ‎∴∠EFO＝∠GOF+∠GPE+∠BEF＝90°+∠NOB+∠BEO，‎ ‎∵∠BOE＝90°﹣∠BON﹣∠BEO，‎ ‎∴2∠EFO+∠BOE＝270°．‎ ‎14．解：（Ⅰ）∵点A（8，0），点C（0，6），OABC为矩形，‎ ‎∴AB＝OC＝6，OA＝CB＝8，∠B＝90°．‎ 根据题意，由折叠可知△AOP≌△AO'P，‎ ‎∴O'A＝OA＝8．‎ 在Rt△AO'B中，BO'＝＝2．‎ ‎∴CO'＝BC﹣BO'＝8﹣2．‎ ‎∴点O'的坐标为（8﹣2，6）．‎ ‎（Ⅱ）①∵∠OAP＝30°，‎ ‎∴∠OPA＝60°，‎ ‎∵∠OPA＝∠O'PA，‎ ‎∴∠CPD＝180°﹣∠OPA﹣∠O'PA＝60°．‎ ‎∵OA＝8，‎ ‎∴OP＝OA•tan30°＝．‎ ‎∴CP＝6﹣OP＝6﹣．‎ ‎∴CD＝CP•tan60°＝6﹣8．‎ ‎∴点D的坐标为（6﹣8，6）．‎ ‎②连接AD，如图：‎ 设CD＝x，则BD＝BC﹣CD＝8﹣x，O'D＝CD＝x，‎ 根据折叠可知AO'＝AO＝8，∠PO'A＝∠POA＝90°，‎ ‎∴在Rt△ADO'中，AD2＝AO'2+DO'2＝82+x2＝x2+64；‎ 在Rt△ABD中，AD2＝BD2+AB2＝（8﹣x）2+62＝x2﹣16x+100；‎ ‎∴x2+64＝x2﹣16x+100，‎ 解得：x＝，‎ ‎∴CD＝，‎ ‎∴D（，6）．‎ ‎15．解：（1）如图1，作AE⊥BC于E，DF⊥BC于F，则AE∥DF，‎ ‎∵AD∥BC，AE⊥BC，‎ ‎∴四边形ADFE是矩形，‎ ‎∴AE＝DF，AD＝EF＝6，‎ 在Rt△ABE和Rt△DCF中，‎ ‎，‎ ‎∴Rt△ABE≌Rt△DCF（HL），‎ ‎∴BE＝CF，‎ ‎∴BE＝CF＝＝3，‎ 由勾股定理得，AE＝＝＝4，‎ 梯形ABCD的面积＝×（AD+BC）×AE＝×（12+6）×4＝36，‎ 故答案为：36；‎ ‎（2）如图3，过D作DE∥AB，交BC于点E，‎ ‎∵AD∥BC，DE∥AB，‎ ‎∴四边形ABED为平行四边形，‎ ‎∴BE＝AD＝6，‎ ‎∴EC＝6，‎ 当PQ∥AB时，PQ∥DE，‎ ‎∴△CQP～△CED，‎ ‎∴，即＝，‎ 解得，t＝；‎ ‎（3）如图2，过G作GH⊥BC，延长HG交AD于I，过E作EX⊥BC，延长XE交AD于Y，过F作FU⊥BC于U，延长UF交AD于W，‎ ‎∵BM＝CN＝5，‎ ‎∴MN＝12﹣5﹣5＝2，‎ ‎∴BN＝CM＝7，‎ ‎∵MN∥AD，‎ ‎∴△MGN～△DGA，‎ ‎∴＝，即＝，‎ 解得，HG＝1，‎ 设AK＝x，‎ ‎∵AD∥BC，‎ ‎∴△BEN～△KEA，‎ ‎∴＝，即＝，‎ 解得，EX＝，‎ 同理：FU＝，‎ S＝S△BKC﹣S△BEN﹣S△CFM+S△MNG ‎＝×12×4﹣×7×﹣×7×+×2×1‎ ‎＝，‎ 当x＝3时，S的最大值为25﹣＝5.4．‎ ‎16．解：（1）∵DF∥BC，EF∥AB，‎ ‎∴∠AFD＝∠ACB，∠DAF＝∠EFC，‎ ‎∴△ADF∽△FEC，‎ ‎∵△ADF、△EFC的面积分别为3，1，‎ ‎∴，‎ ‎∴，‎ ‎∵△ADF的边DF上的高为h1，△EFC的边CE上的高为h2，‎ ‎∴；‎ 故答案为：．‎ ‎（2）证明：如图①，设AD＝a，BD＝b，DB与EF间的距离为h，‎ ‎∵EF∥AB，DF∥BC，‎ ‎∴四边形DBFE是平行四边形，‎ ‎∴BD＝EF＝b，‎ 由（1）知△ADF∽△FEC，‎ ‎∴，‎ ‎∵S1＝ah，‎ ‎∴S2＝，‎ ‎∴S1S2＝，‎ ‎∴bh＝2，‎ ‎∵S＝bh，‎ ‎∴S＝2．‎ ‎（3）如图②，过点D作DM∥AC交BC于点M，‎ ‎∴∠DMF＝∠ECG，‎ ‎∵DE∥BC，DF∥BG，‎ ‎∴四边形DFGE为平行四边形，‎ ‎∴∠DF＝EG，∠DFM＝∠EGC，‎ ‎∴△DFM≌△EGC（AAS），‎ ‎∴S△DFM＝S△EGC＝5，‎ ‎∵S△DBF＝7，‎ ‎∴S△BDM＝7+5＝12，‎ ‎∵DE∥BM，DM∥AC，‎ ‎∴∠ADE＝∠DBM，∠BDM＝∠BAE，‎ ‎∴△DAE∽△BDM，‎ ‎∴＝，‎ ‎∴，‎ ‎∴，‎ 同理，△ADE∽△ABC，‎ ‎∴S△ABC＝9S△ADE＝9×3＝27．‎ ‎17．解：（1）当PQ∥AD时，∵DC∥AB，‎ ‎∴四边形APQD是平行四边形，‎ ‎∴AP＝DQ，即2t＝4+t，‎ 解得，t＝4，‎ ‎∴当t为4s时，PQ∥AD；‎ ‎（2）过点D作DF⊥AB于F，过点E作EM⊥AB于M，延长ME交CD的延长线于点N，‎ ‎∴∠DFA＝∠DFB＝90°，∠EMA＝∠EMB＝90°，‎ ‎∵AB∥CD，‎ ‎∴∠CDF＝90°，∠CNM＝90°，‎ ‎∵∠ABC＝90°，‎ ‎∴四边形DFBC、NMFD是矩形，‎ ‎∴BF＝DC＝4，‎ ‎∴AF＝6，‎ ‎∴DF＝＝8，‎ ‎∴MN＝BC＝DF＝8，‎ ‎∵PE∥BD，‎ ‎∴，‎ ‎∵AB＝AD，‎ ‎∴AE＝AP＝2t，‎ ‎∵∠A＝∠A，∠EMA＝∠DFA，‎ ‎∴△AEM∽△ADF，‎ ‎∴，即，‎ ‎∴，‎ ‎∴，‎ ‎∴y＝S四边形PBQE＝S梯形ABQD﹣S△AEP﹣S△QED ‎＝＝‎ ‎＝﹣t2+t+40，‎ ‎∴y与的函数关系式为：y═﹣t2+t+40（0＜t＜5）；‎ ‎（3）假设存在某一时刻t，四边形PBQE的面积为四边形ABQD面积的，‎ 则﹣t2+t+40＝××（4+t+10）×8，‎ 解得，t1＝4，t2＝﹣（不合题意，舍去），‎ 答：当t＝4时，四边形PBQE的面积为四边形ABQD面积的；‎ ‎（4）若存在某一时刻t，使EQ⊥BD，垂足为O，‎ ‎∴∠DOE＝∠DOQ＝90°，‎ ‎∵AB∥CD，‎ ‎∴∠BDC＝∠DBA，‎ ‎∵AB＝AD，‎ ‎∴∠BDA＝∠DBA，‎ ‎∴∠BDC＝∠BDA，‎ ‎∴DE＝DQ，‎ ‎∴4+t＝10﹣2t，‎ ‎∴t＝2，‎ ‎∴当t为2s时，EQ⊥BD．‎ ‎18．解：（1）如图1中，作PH⊥BC于H．‎ ‎∵四边形ABCD是菱形，‎ ‎∴AB＝BC＝4，AD∥BC，‎ ‎∴∠A+∠ABC＝180°，‎ ‎∵∠A＝120°，‎ ‎∴∠PBH＝60°，‎ ‎∵PB＝3，∠PHB＝90°，‎ ‎∴BH＝PB•cos60°＝，PH＝PB•sin60°＝，‎ ‎∴CH＝BC﹣BH＝4﹣＝，‎ ‎∴PC═＝＝．‎ ‎（2）如图1中，作PH⊥BC于H，连接PQ，设PC交BD于O．‎ ‎∵四边形ABCD是菱形，‎ ‎∴∠ABD＝∠CBD＝30°，‎ ‎∵∠PCQ＝30°，‎ ‎∴∠PBO＝∠QCO，‎ ‎∵∠POB＝∠QOC，‎ ‎∴△POB∽△QOC，‎ ‎∴，‎ ‎∴，‎ ‎∵∠POQ＝∠BOC，‎ ‎∴△POQ∽△BOC，‎ ‎∴∠OPQ＝∠OBC＝30°＝∠PCQ，‎ ‎∴PQ＝QC，‎ ‎∴PC＝QC，‎ 在Rt△PHB中，BP＝n，‎ ‎∴BH＝n，PH＝n，‎ ‎∵PC2＝PH2+CH2，‎ ‎∴3QC2＝（n）2+（4﹣n）2，‎ ‎∴QC＝（0≤n＜8）．‎ ‎（3）①如图2中，若直线QP交直线BC于B点左侧的点E．‎ 此时∠CQE＝120°，‎ ‎∵∠PBC＝60°，‎ ‎∴△PBC中，不存在角与∠CQE相等，‎ 此时△QCE与△BCP不可能相似．‎ ‎②如图3中，若直线QP交直线BC于点C右侧的点E．‎ 则∠CQE＝∠B＝QBC+∠QCP＝60°＝∠CBP，‎ ‎∵∠PCB＞∠E，‎ ‎∴只可能∠BCP＝∠QCE＝75°，‎ 作CF⊥AB于F，则BF＝2，CF＝2，∠PCF＝45°，‎ ‎∴PF＝CF＝2，‎ 此时BP＝2+2，‎ ‎③如图4中，当点P在AB的延长线上时，‎ ‎∵△CBE与△CBP相似，‎ ‎∴∠CQE＝∠CBP＝120°，‎ ‎∴∠QCE＝∠CBP＝15°，‎ 作CF⊥AB于F．‎ ‎∵∠FCB＝30°，‎ ‎∴∠FCB＝45°，‎ ‎∴BF＝BC＝2，CF＝PF＝2，‎ ‎∴BP＝2﹣2．‎ 综上所述，满足条件的BP的值为2+2或2﹣2．‎ ‎19．解：（1）①∵∠ACB＝90°，AC＝12，AB＝20，‎ ‎∴BC＝＝＝16，‎ 故答案为：16；‎ ‎②∵sinB＝，‎ ‎∴，‎ ‎∴PQ＝3t，‎ 故答案为：3t；‎ ‎（2）在Rt△PQB中，BQ＝＝4t，‎ 当点M与点Q相遇，20＝4t+5t，‎ ‎∴t＝，‎ 当0＜t＜时，MQ＝AB﹣AM﹣BQ，‎ ‎∴20﹣4t﹣5t＝10，‎ ‎∴t＝，‎ 当＜t≤时，MQ＝AM+BQ﹣AB，‎ ‎∴4t+5t﹣20＝10，‎ ‎∴t＝，‎ ‎∵＞，‎ ‎∴不合题意舍去，‎ 综上所述：当QM的长度为10时，t的值为；‎ ‎（3）当0＜t＜时，S＝3t×（20﹣9t）＝﹣27t2+60t；‎ 当＜t≤时，如图，‎ ‎∵四边形PQMN是矩形，‎ ‎∴PN＝QM＝9t﹣20，PQ＝3t，PN∥AB，‎ ‎∴∠B＝∠NPE，‎ ‎∴tanB＝tan∠NPE，‎ ‎∴，‎ ‎∴NE＝＝﹣15，‎ ‎∴S＝3t×（9t﹣20）﹣×（9t﹣20）×（﹣15）＝﹣；‎ ‎（4）如图，若NQ⊥AC，‎ ‎∴NQ∥BC，‎ ‎∴∠B＝∠MQN，‎ ‎∴tanB＝tan∠MQN，‎ ‎∴，‎ ‎∴＝，‎ ‎∴t＝，‎ 如图，若NQ⊥BC，‎ ‎∴NQ∥AC，‎ ‎∴∠A＝∠BQN，‎ ‎∴tanA＝tan∠BQN，‎ ‎∴，‎ ‎∴，‎ ‎∴t＝‎ 综上所述：当t＝或时，过点Q和点N的直线垂直于Rt△ABC的一边．‎ ‎20．（1）证明：设BE与AF交于点H，如图1所示：‎ ‎∵四边形ABCD是正方形，‎ ‎∴AB∥CD，∠BAE＝∠ADF＝90°，AB＝AD，‎ 在△BAE和△ADF中，，‎ ‎∴△BAE≌△ADF（SAS），‎ ‎∴∠ABE＝∠DAF，‎ ‎∴∠DAF+∠AEB＝∠ABE+∠AEB＝90°，‎ ‎∴∠AHE＝90°，‎ ‎∴BE⊥AF；‎ ‎（2）证明：∵KS∥AF，‎ ‎∴，‎ ‎∵AB∥CD，‎ ‎∴△DGF∽△BGA，‎ ‎∴，‎ ‎∵AK＝AE，AE＝DF，‎ ‎∴AK＝DF，‎ ‎∴＝，‎ ‎∴GS＝DG，‎ ‎∴G是SD中点；‎ ‎（3）解：作EP⊥BD于P，如图2所示：‎ ‎∵BE是∠ABD的平分线，EA⊥AB，‎ ‎∴AE＝PE，‎ ‎∵四边形ABCD是正方形，‎ ‎∴AD＝AB＝8，∠BAD＝90°，∠ABD＝∠ADB＝45°，‎ ‎∴BD＝AB＝8，‎ ‎∵EP⊥BD，‎ ‎∴△PDE是等腰直角三角形，‎ ‎∴PD＝PE，DE＝PE＝PD，‎ ‎∴AE＝PE＝PD，‎ ‎∵AE+DE＝AD＝8，‎ ‎∴AE+AE＝8，‎ 解得：AE＝8﹣8，‎ ‎∴DF＝AE＝AK＝8﹣8，‎ ‎∴BK＝AB﹣AK＝8﹣（8﹣8）＝16﹣8，‎ ‎∵AB∥CD，‎ ‎∴△DGF∽△BGA，‎ ‎∴＝＝＝+1，‎ ‎∴DG＝＝＝8﹣8，‎ ‎∴BS＝BD﹣2DG＝8﹣2（8﹣8）＝16﹣8，‎ 作SN⊥AB于N，则△BNS是等腰直角三角形，‎ ‎∴SN＝BN＝BS＝8﹣8，‎ ‎∴△BSK的面积＝BK×SN＝×（16﹣8）×（8﹣8）＝96﹣128．‎