图形的位似教案2 3页

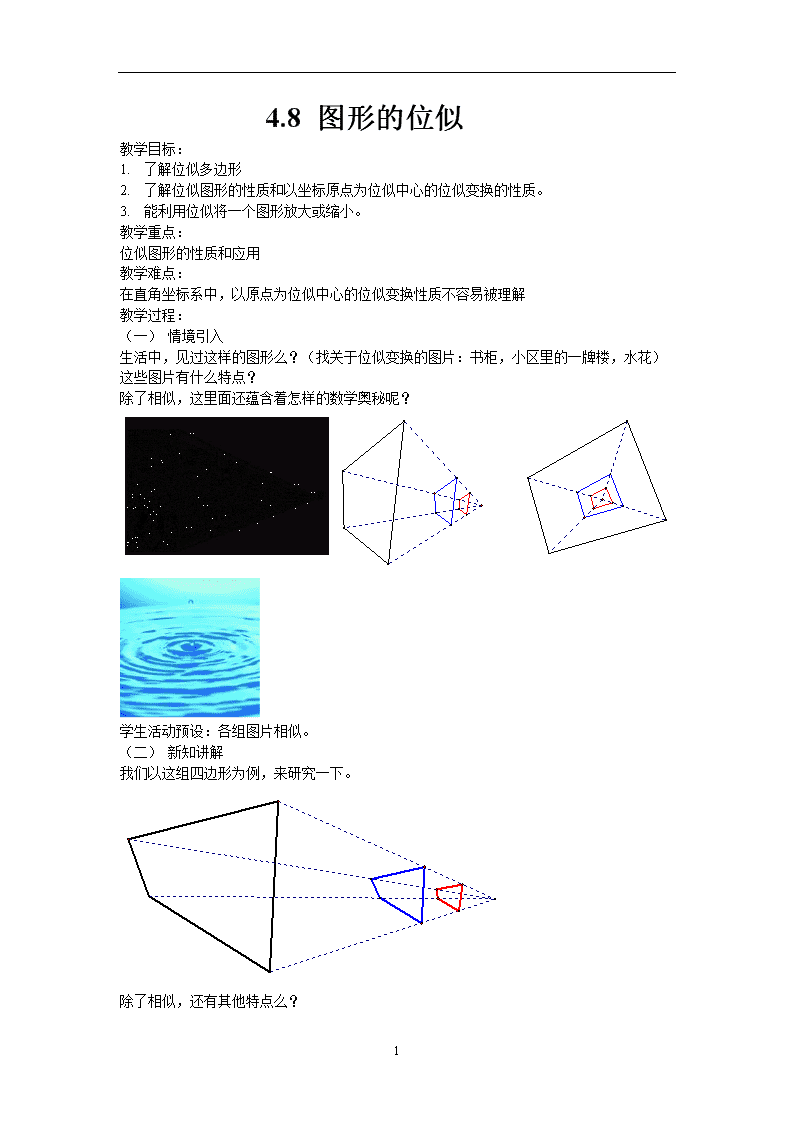
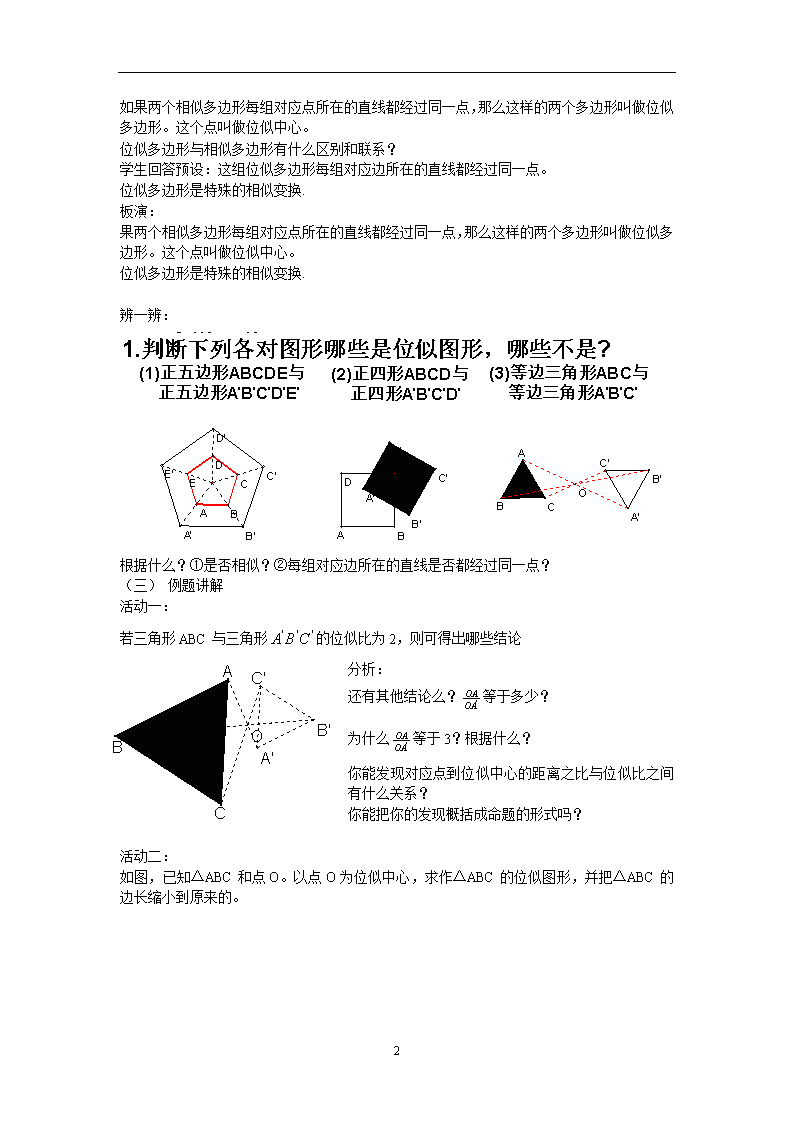
‎4.8 图形的位似 教学目标：‎ 1. 了解位似多边形 2. 了解位似图形的性质和以坐标原点为位似中心的位似变换的性质。‎ 3. 能利用位似将一个图形放大或缩小。‎ 教学重点：‎ 位似图形的性质和应用 教学难点：‎ 在直角坐标系中，以原点为位似中心的位似变换性质不容易被理解 教学过程：‎ （一） 情境引入 生活中，见过这样的图形么？（找关于位似变换的图片：书柜，小区里的一牌楼，水花）‎ 这些图片有什么特点？‎ 除了相似，这里面还蕴含着怎样的数学奥秘呢？‎ 学生活动预设：各组图片相似。‎ （二） 新知讲解 我们以这组四边形为例，来研究一下。‎ 除了相似，还有其他特点么？‎ 3‎ 如果两个相似多边形每组对应点所在的直线都经过同一点，那么这样的两个多边形叫做位似多边形。这个点叫做位似中心。‎ 位似多边形与相似多边形有什么区别和联系？‎ 学生回答预设：这组位似多边形每组对应边所在的直线都经过同一点。‎ 位似多边形是特殊的相似变换.‎ 板演：‎ 果两个相似多边形每组对应点所在的直线都经过同一点，那么这样的两个多边形叫做位似多边形。这个点叫做位似中心。‎ 位似多边形是特殊的相似变换.‎ 辨一辨：‎ 根据什么？①是否相似？②每组对应边所在的直线是否都经过同一点？‎ （一） 例题讲解 活动一：‎ 若三角形ABC与三角形的位似比为2，则可得出哪些结论 分析：‎ 还有其他结论么？等于多少？‎ 为什么等于3？根据什么？‎ 你能发现对应点到位似中心的距离之比与位似比之间有什么关系？‎ 你能把你的发现概括成命题的形式吗？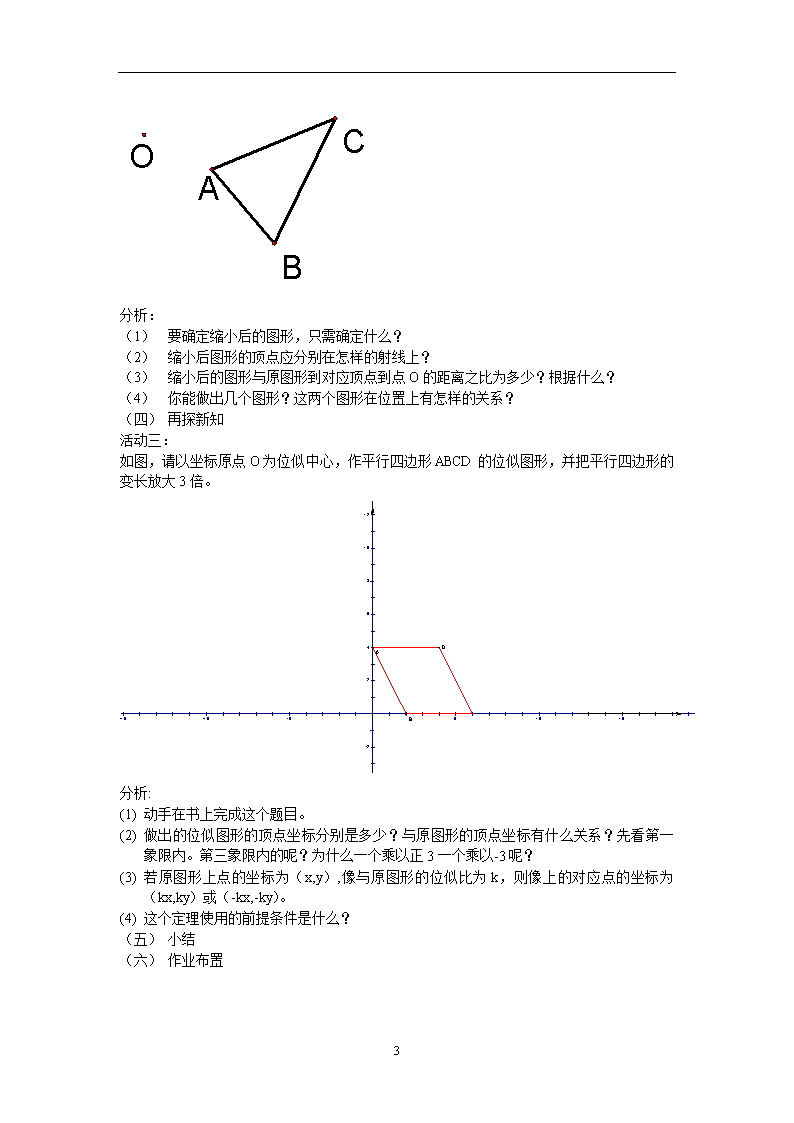‎ 活动二：‎ 如图，已知△ABC和点O。以点O为位似中心，求作△ABC的位似图形，并把△ABC的边长缩小到原来的。‎ 3‎ 分析：‎ （1） 要确定缩小后的图形，只需确定什么？‎ （2） 缩小后图形的顶点应分别在怎样的射线上？‎ （3） 缩小后的图形与原图形到对应顶点到点O的距离之比为多少？根据什么？‎ （4） 你能做出几个图形？这两个图形在位置上有怎样的关系？‎ （一） 再探新知 活动三：‎ 如图，请以坐标原点O为位似中心，作平行四边形ABCD的位似图形，并把平行四边形的变长放大3倍。‎ 分析:‎ (1) 动手在书上完成这个题目。‎ (2) 做出的位似图形的顶点坐标分别是多少？与原图形的顶点坐标有什么关系？先看第一象限内。第三象限内的呢？为什么一个乘以正3一个乘以-3呢？‎ (3) 若原图形上点的坐标为（x,y）,像与原图形的位似比为k，则像上的对应点的坐标为（kx,ky）或（-kx,-ky）。‎ (4) 这个定理使用的前提条件是什么？‎ （二） 小结 （三） 作业布置 3‎