2013山东威海中考数学试题 12页

2013 年威海市初中学业考试 数学 （满分 120 分，考试时间 120 分钟） 一、选择题（本大题共 12 小题，每小题 3 分，共 36 分，在每小题给出的四个选项中，只有一 个是正确的，每小题选对得 3 分，选错、不选或多选，均不得分） 1．（ 2013 山东威海，1，3 分）花粉的质量很小，一粒某种植物花粉的质量约为 0.000037 毫克， 已知 1 克=1000 毫克，那么 0.000037 毫克可以用科学计数法表示为（ ） A．3.7×10-5 克 B．3.7×10-6 克 C．3.7×10-7 克 D．3.7×10-8 克 【答案】D 2．（ 2013 山东威海，2，3 分）下列各式化简结果为无理数的是（ ） A． 3 -27 B． ( 2 -1)0 C． 8 D． 2-2（ ） 【答案】C 3．（ 2013 山东威海，3，3 分）下列运算正确的是（ ） A．3x2+4x2=7x4 B．2x3  3x3=6x3 C．x6 x3=x2 D．(x2)4=x8 【答案】D 4．（2013 山东威海，4，3 分）若 m-n = -1，则（m-n）2-2m+2n 的值是（ ） A．3 B．2 C．1 D．-1 【答案】A 5．（ 2013 山东威海，5，3 分）下图是由 6 个同样大小的正方体摆成的几何体.将正方体①移走 后，所得几何体（ ） A．主视图改变，左视图改变 B．俯视图不变，左视图不变 C．俯视图改变，左试图改变 D．主视图改变，左视图不变 【答案】D 6．（ 2013 山东威海，6，3 分）已知关于 x 的一元二次方程（x+1）2-m=0 有两个实数根.则 m 的取值范围是（ ） A． m  3- 4 B． m 0 C． m 1 D． m 2 【答案】B 7．（ 2013 山东威海，7，3 分）不等式 20 21 x x    的解集在数轴上表示为（ ） 【答案】B 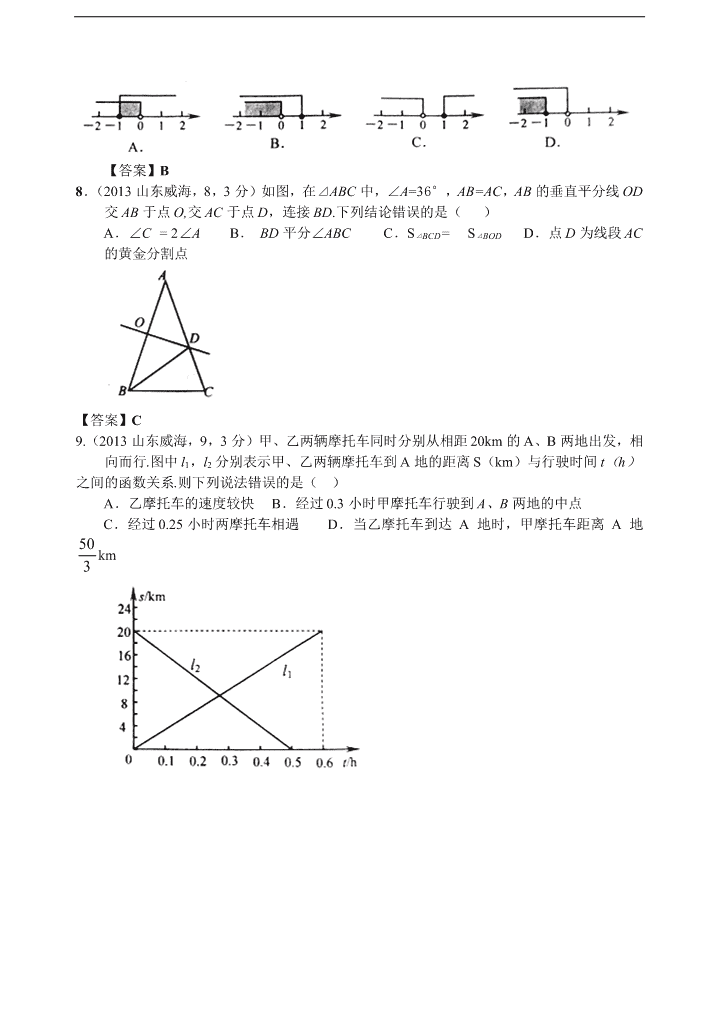8．（ 2013 山东威海，8，3 分）如图，在⊿ABC 中，∠A=36°，AB=AC，AB 的垂直平分线 OD 交 AB 于点 O,交 AC 于点 D，连接 BD.下列结论错误的是（ ） A．∠C = 2∠A B． BD 平分∠ABC C．S⊿BCD= S⊿BOD D．点 D 为线段 AC 的黄金分割点 【答案】C 9.（2013 山东威海，9，3 分）甲、乙两辆摩托车同时分别从相距 20km 的 A、B 两地出发，相 向而行.图中 l1，l2 分别表示甲、乙两辆摩托车到 A 地的距离 S（km）与行驶时间 t（h） 之间的函数关系.则下列说法错误的是（ ） A．乙摩托车的速度较快 B．经过 0.3 小时甲摩托车行驶到 A、B 两地的中点 C．经过 0.25 小时两摩托车相遇 D．当乙摩托车到达 A 地时，甲摩托车距离 A 地 50 3 km 【答案】C 10．（ 2013 山东威海，10，3 分）如图，在⊿ABC 中，∠ACB=90°，BC 的垂直平分线 EF 交 BC 于点 D，交 AB 于点 E，且 BE=BF.添加一个条件，仍不能证明四边形 BECF 为正方形的是 （ ） A． BC=AC B．CF⊥BF C． BD=DF D． AC=BF 【答案】D 11．（ 2013 山东威海，11，3 分）一个不透明的袋子里装着质地、大小都相同的 3 个红球和 2 个绿球，随机从中摸出一球，不再放回袋中，充分搅匀后再随机摸出一球.两次都摸到红球的 概率是（ ） A． 3 10 B． 9 25 C． 9 20 D． 3 5 【答案】A 12．（ 2013 山东威海，12，3 分）如图，在平面直角坐标系中，∠AOB=90°，∠OAB=30°， 反比例函数 y1= m x 的图像经过点 A,反比例函数 2 ny x 的图像经过点 B，则下列关于 m，n 的关系正确的是（ ） A．m=-3n B．m=- 3 n C．m=- 3 3 n D．m= 【答案】A 二、填空题（本大题共 6 小题，每小题 3 分，共 18 分.只要填出最后结果） 13（2013 山东威海，13，3 分）.将一副直角三角板如图摆放,点 C 在 EF 上,AC 经过点 D,已知 ∠A=∠EDF=90°,AB=AC, ∠A=30°, ∠BCE=40°,则∠CDF= . 【答案】25° 14. （2013 山东威海，14，3 分）分解因式：-3x2+2x- 3 1 = . 【答案】 21- 3x-13 （ ） 15. （2013 山东威海，15，3 分）如图，AC⊥CD,垂足为点 C，BD⊥CD,垂足为点 D, AB 与 CD 交于点 O，若 AC=1，BD=2，CD=4，则 AB= . 【答案】5 16（2013 山东威海，16，3 分）.若关于 x 的方程 1 5 10 2 xm xx   无解,则 m= . 【答案】-8 17. （2013 山东威海，17，3 分）如图①,将四边形纸片 ABCD 沿两组对边中点连线剪切为四 部分，将这四部分密铺可得到如图②所示的平行四边形.若要使密铺后的平行四边形为矩形,则 四边形 ABCD 需要满足的条件是 。 【答案】AC=BD 18. （2013 山东威海，18，3 分）如图,在平面直角坐标系中,点 A,B,C 的坐标分别为 (1,0),(0,1),(-1,0).一个电动玩具从坐标原点 O 出发,第一次跳跃到点 P1,使得点 P1 与点 O 关于点 A 成中心对称;第二次跳跃到点 P2,使得点 P2 与点 P1 关于点 B 成中心对称; 第三次跳跃 到点 P3,使得点 P3 与点 P2 关于点 C 成中心对称; 第四次跳跃到点 P4,使得点 P4 与点 P3 关于点 A 成中心对称; 第五次跳跃到点 P5,使得点 P5 与点 P4 关于点 B 成中心对称;.…照此规律重复下 去，则点 P2013 的坐标为 . 【答案】(0,-2) 三.解答题 19. （2013 山东威海，19，7 分）先化简,再求值: 2 2 1 x +2x+1-1x-1 x -1  ,其中 x= 2-1 【答案】解:原式= 21-x+1 x+1) x-1 x+1 （ （ ）(x-1)= 2 2 ( 1)( 1) 1 ( 1) x x x xx    = 2 1 x x   把 21x 代入上式， 2 2 1 2 3 2 3 2 1122 1 1 2 x x           20. （2013 山东威海，20，8 分）如图，CD 为⊙O 的直径，CD⊥AB，垂足为 F，AO⊥BC, 垂足为点 E,AO=1. （1）求∠C 的大小 （2）求阴影部分的面积 【答案】解:(1)∵CD 为⊙O 的直径, CD⊥AB ∴ ∠C= 1 2 ∠AOD ∵∠AOD=∠COE, ∴∠C= ∠COE ∵AO⊥BC ∴∠C=30° (2)连接 OB.由（1）知∠C=30° ∴ ∠AOD=60° ∴ ∠AOB=120° 在 Rt△AOF 中，AO=1，∠AOF=60° ∴AF= 3 2 ，OF= 1 2 . ∴AB= 3 ∴S 阴影=S 扇形 OAB-S⊿OAB= 2120 1 1 1 31 - 3= -360 2 2 3 4   21．（ 2013 山东威海，21，9 分）某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩 的原始分满分均为 100 分.前六名选手的得分如下: 序号 项目 1 2 3 4 5 6 笔试成绩/分 85 92 84 90 84 80 面试成绩/分 90 88 86 90 80 85 根据规定，笔试成绩和面试成绩分别按一定的百分比折合成综合成绩（综合成绩的满分仍 为 100 分） （1）这 6 名选手笔试成绩的中位数是 分，众数是 分； （2）现得知 1 号选手的综合成绩为 88 分，求笔试成绩和面试成绩各占的百分比； （3）求出其余 5 名选手的综合成绩，并以综合成绩排序确定前两名人选. 【答案】解（1）84.5, 84 （2）设笔试成绩和面试成绩所占的百分比分别为 x，y，由题意得 1 85 90 88 xy xy    解这个方程组，得 0.4 0.6 x y    ∴笔试成绩和面试成绩所占的百分比分别为 40%和 60% （3）2 号选手的综合成绩=92×0.4+88×0.6=89.6（分） 3 号选手的综合成绩=84×0.4+86×0.6=85.2（分） 4 号选手的综合成绩=90×0.4+90×0.6=90（分） 5 号选手的综合成绩=84×0.4+80×0.6=81.6（分） 6 号选手的综合成绩=80×0.4+85×0.6=83（分） ∴综合成绩最高的两名选手是 4 号和 2 号 22．（ 2013 山东威海，22，9 分）如图，已知抛物 y=x2+bx+c 与 x 轴交于点 A、B，AB=2，与 y 轴交于点 C，对称轴为直线 x=2. （1）求抛物线的函数表述式； （2）设 P 为对称轴上一动点，求△APC 周长的最小值； （3）设 D 为抛物线上一点，E 为对称轴上一点，若以点 A、B、D、E 为顶点的四边形是菱形， 则点 D 的坐标为 . 【答案】解：（1）∵AB=2，对称轴为直线 x=2 ∴ A 点的坐标为（1,0）， B 点的坐标为（3,0） ∵抛物 y=x2+bx+c 与 x 轴交于点 A、B ∴1,3 是方程 x2+bx+c=0 的两个根. 由根与系数的关系，得 1+3=-b，1×3=c ∴b=-4，c=3 ∴抛物线的函数表达式为 y=x2-4x+3 （2）连接 AC，BC，BC 交对称轴于点 P，连接 PA. 由（1）知抛物线的函数表达式为 y=x2-4x+3，点 A、B 的坐标分别为（1,0），（ 3,0） ∴ 点 C 的坐标为（0,3）. ∴ BC= 223 +3 =3 2 ，AC= 223 +1 = 10. ∵点 A、B 关于对称轴 x=2 对称，∴PA=PB ∴PA+PC=PB+PC 此时，PB+PC=BC ∴当 P 点在对称轴上运动时，PA+PC 的最小值等于 BC ∴△APC 周长的最小值=AC+AP+PC=3 2+ 10 （3）（ 2，-1） 23．（ 2013 山东威海，23，10 分）要在一块长 52m，宽 48m 的矩形绿地上，修建同样宽的两 条互相垂直的甬路.下面分别是小亮和小颖的设计方案. （1） 求小亮设计方案中甬路的宽度 x （2） 求小颖设计方案中四块绿地的总面积（友情提示：小颖设计方案中的 x 与小亮设计 方案中 x 的取值相同） 【答案】解：（1）根据小亮的设计方案列方程,得: (52-x)（48-x）=2300. 解这个方程，得：x1=2，x2=98（舍去） ∴小亮设计方案中甬路的宽度为 2m. （2） 作 AI⊥CD，HJ⊥EF，垂足分别为 I,J ∵AB∥CD，∠1=60° ∴ ∠ADI=60° ∵BC∥AD, ∴四边形 ADCB 为平行四边形. ∴BC=AD. 由（1）得 x=2， ∴BC=HE=2=AD 在 Rt⊿ADI 中，AI=2sin60°= 3 . ∵∠HEJ=60° ∴HJ=2sin60°= ∴小颖设计方案中四块绿地的总面积=52×48-52×2-48×2+（ 3 ）2=2299（m2） 24．（ 2013 山东威海，24，11 分）操作发现 将一副直角三角板如图①摆放，能够发现等腰直角三角板 ABC 的斜边 BC 与含 30°角的 直角三角板 DEF 的长直角边 DE 重合 问题解决 将图①中的等腰直角三角板 ABC 绕点 B 顺时针旋转 30°，点 C 落在 BF 上.AC 与 BD 交 于点 O，连接 CD，如图② (1)求证：△CDO 是等腰三角形； （2）若 DF=8，求 AD 的长 【答案】解：（1）由图①知 BC=DE，∴∠BDC=∠BCD ∵∠DEF=30°，∴ ∠BDC=∠BCD=75° ∵∠ACB=45° ∴∠DOC=30°+45°=75° ∴∠DOC=∠BDC ∴△CDO 是等腰三角形 （2）作 AG⊥BC，垂足为点 G.DH⊥BF，垂足为点 H 在 Rt△DHF 中，∠F=60°，DF=8，∴DH=4 3 ，HF=4 在 Rt△BDF 中，∠F=60°，DF=8，∴BD=8 ，BF=16 ∴ BC=BD=8 3 ∵AG⊥BC, ∠ABC=45° ∴AG=DH ∵AG∥DH, ∴四边形 AGHD 为矩形. ∴ AD=GH=BF-BG -HF=16-4 -4=12-4 25．（2013 山东威海，25，12 分）如图，在平面直角坐标系中，直线 y= 1 2 x+ 3 2 与直线 y=x 交于点 A，点 B 在直线 y= x+ 上，∠BOA=90°,.抛物线 y=ax2+bx+c 过点 A,O ,B,顶点 为 E. （1） 求点 A，B 的坐标 （2） 求抛物线的函数表达式及顶点 E 的坐标； （3） 设直线 y=x 与抛物线的对称轴交与点 C,直线 BC 交抛物线于点 D，过点 E 作 FE∥x 轴，交直线 AB 于点 F，连接 OD，CF，CF 交 x 轴于点 M. (3)试判断 OD 与 CF 是否平行，并说明理由 【答案】解：（1）由直线 y= x+ 与直线 y=x 交于点 A，得 13 22 yx yx   解这个方程组得 3 3 x y    ∴ 点 A 的坐标为（3,3） 作 AG⊥x 轴，垂足为点 G.，作 BH⊥x 轴，垂足为点 H ∵∠BOA=90°，∴ ∠BOH+∠AOG=90° ∵∠OAG+∠AOG=90° ∴∠OAG=∠BOH ∵∠BHO=∠AGO=90° ∴⊿BHO ∽⊿OGA ∴ BH OH OG AG . ∵OG=AG=3， ∴BH=OH 设点 B 的坐标为（-m，m），代入 y= 1 2 x+ 3 2 ，得 m= 13()22m. 解，得 m=1，,∴点 B 的坐标为（-1,1） （2）∵抛物线 y=ax2+bx+c 经过原点 O , ∴C=0 由抛物线过点 A（3,3）， B（-1,1）两点，可得 9 3 3 1 ab ab    解，得 1 2 1 2 a b     ∴抛物线的表达式为 211 22y x x ∴抛物线顶点 E 坐标为（ 11,28 ）. （3） OD∥CF 由（2）可知，抛物线的对称轴为直线 1 2x  ， ∵直线 y=x 与抛物线的对称轴交与点 C, ∴点 C 的坐标为（ 11,22 ）. 设直线 BC 的表达式为 y kx b，把 B（-1 , 1），C（ ）代入，得 1 11 22 kb kb     解，得 1 3 2 3 k b     ∴直线 BC 的表达式为 12 33yx   ∵直线 BC 与抛物线交于点 B，点 D， ∴ 21 2 1 1 3 3 2 2x x x    .解得 21 4 ,13xx   把 1 4 3x  代入 ，得 1 2 9y  .∴点 D 的坐标为（ 42,39 ）. 作 DN⊥x 轴，垂足为点 N ∴tan∠DON= DN ON = 1 6 ∵FE∥x 轴，点 E 坐标为（ 11,28 ），∴点 F 的纵坐标为 1 8 把.y= 代入 y= 1 2 x+ 3 2 ，得 x+ = .解，得 13 4x  . ∴点 F 的坐标为（ 13 1,48）. ∴EF= 1 13 15 2 4 4 ∵CE= 1 1 5 2 8 8 ∴tan∠CFE= 1 6 CE EF  .∴∠CFE=∠DON. 又 FE∥x 轴, ∴∠CMN=∠CFE ∴∠CMN=∠DON ∴ OD∥CF