二次函数y=ax2+bx+c的图象教案4 6页

‎2.4 二次函数的图象 ‎【教学目标】‎ ‎ 1．会用描点法画出二次函数的图象，进一步了解抛物线的概念．‎ ‎ 2．了解抛物线的顶点、开口方向、对称轴的关概念．‎ ‎ 3．会求二次函数的最大值或最小值．‎ ‎ 4．理解二次函数，函数值随自变量的变化规律.‎ ‎ 5．会用二次函数的性质解决有关简单的实际问题.‎ ‎【重点、难点】‎ ‎ 重点：会画二次函数的图象，及理解二次函数的关性质.‎ ‎ 难点：会用二次函数的有关性质解决一些简单的实际问题.‎ ‎【知识要点 ‎ 1．二次函数的图象画法．‎ ‎ 方法一，用“列表、描点、连线”方法来画；‎ ‎ 方法二，将二次函数的图象向上或向下平移个单位.当时，向上平移个单位；当时，向下平移-个单位.‎ ‎ 2．二次函数的性质 ‎ 二次函数的性质，见下表：‎ 函 数 图 象 ‎ ‎ 开口 方向 顶点 坐标 对称轴 函数变化 最大（小）值 向上 ‎（0，c）‎ 轴 时，随增大而增大； 时，随增大而减小.‎ 当时，‎ ‎.‎ 向下 ‎（0，c）‎ 轴 时，随增大而减小； 时，随增大而增大.‎ 当时，‎ ‎.‎ ‎ 3．利用二次函数的性质解有关简单的实际问题.‎ ‎ （1）根据题意建立二次函数关系式，并注意其定义域；‎ 6‎ ‎ （2）应用二次函数的性质解决相关的实际问题.‎ 引入：．在同一坐标系中画出图象y=x，y=x+1，y=x－3，并说出它们的位置关系。‎ 通过作图我们可以得出如下的结论：‎ 性质1： y=ax+c的图象与y=ax的图象形状---------‎ ‎ ①其对称轴为----轴 ‎ ②顶点坐标为（-------,--------）‎ ‎ ③当a>0时，开口-----，图象y=ax有最---点；当x=0时，y有最---值为----；当a<0时，开口---，图象有最----点，当x=0时，y有最大值为c ‎ ④当c>0时，是由y=ax向-----平移c个单位，当c<0时，是由y=ax向----平移|c|个单位。简称“--------------------”‎ ‎【经典例题】‎ 例1．（1）抛物线y=－的顶点坐标是 ，对称轴是 。‎ ‎（2）y=2x－8的顶点坐标是 ，对称轴是 ，开口方向 ，当x= 时，y有最 值为 ，这是由y=2x 得到的。‎ ‎（3）y=－8x沿y轴向上平移4个单位得y= ，其对称轴为 ，顶点坐标为 。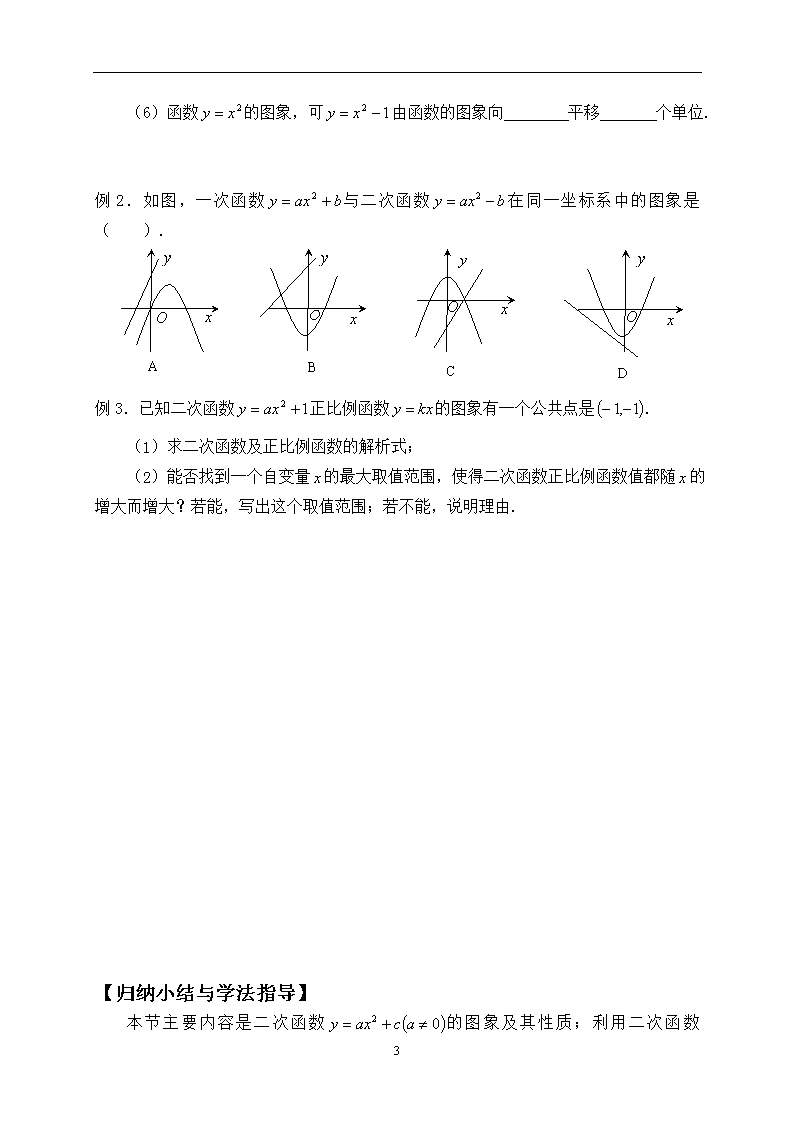‎ ‎（4）与抛物线y=－形状相同，开口方向相同，而顶点在抛物线y=－的顶点上方3个单位的抛物线所对应的函数是： ‎ ‎（5）已知函数y=ax与 函数y=－+c的图象形状相同，且将抛物线y=ax沿对称轴平移2个单位就得到与抛物线y=－+c完全重合，则a= ，c= ‎ 6‎ ‎ （6）函数的图象，可由函数的图象向 平移 个单位.‎ 例2．如图，一次函数与二次函数在同一坐标系中的图象是（ ）.‎ C D B A 例3．已知二次函数正比例函数的图象有一个公共点是.‎ ‎ （1）求二次函数及正比例函数的解析式；‎ ‎ （2）能否找到一个自变量的最大取值范围，使得二次函数正比例函数值都随的增大而增大？若能，写出这个取值范围；若不能，说明理由.‎ ‎【归纳小结与学法指导】‎ ‎ 本节主要内容是二次函数的图象及其性质；利用二次函数 6‎ 的图象及性质解决一些简单的实际问题.‎ ‎ 学习二次函数的图象及性质要与二次函数的图象及性质进行类比，这样便于理解和掌握，实际上二次函数的图象可由二次函数的图象向上或向下平移而得到.它们的性质除顶点以外，其他性质都相同.‎ ‎【课堂练习】‎ 一．选择题：‎ ‎ 1．已知二次函数，自变量在什么范围内，（ ）.‎ ‎ A、 B、 C、 D、为一切实数 ‎ 2．函数的性质有（ ）.‎ ‎ A、当为任何实数时，值总为正 ‎ B、当值增加时，值也增加 ‎ C、它的图象关于轴对称 ‎ D、它的图象在第一、三象限内 ‎ 3．在平面直角坐标系中，抛物线与直线相交于两点，已知点的坐标是，则点坐标是（ ）.‎ ‎ A、 B、 C、 D、‎ ‎ 4．下列四个函数：①；②；③；④.其中，在自变量的允许值范围内，随增大而增大的函数的个数为（ ）个.‎ ‎ A、1 B、2 C、3 D、4‎ ‎ 5．在半径4cm的圆中，挖去一个半径为cm的圆面，剩下圆环的面积为，则与的函数关系为（ ）.‎ ‎ A、 B、‎ ‎ C、 D、‎ A ‎ 6．已知关于的函数关系式为（为正常数，为时间），则函数图象为（ ）.‎ B C D 6‎ ‎7．函数y=ax与y=ax－3的图象大致为( )‎ y x ‎0‎ y x ‎0‎ y x ‎0‎ y x ‎0‎ A B C D 二．填空题：‎ ‎ 1．若抛物线开口向下，则= .‎ ‎ 2．若抛物线顶点位于轴上方，则 .‎ ‎ 3．把函数的图象沿轴对折，得到图象的函数解析式为 .‎ ‎ 4．直线与抛物线在第一象限内的交点坐标是 .‎ ‎ 5．一个长方形周长是50cm，一边长是cm，这个长方形的面积与的函数关系式是 .‎ 三．解答题：‎ ‎ 1．已知是抛物线上的点，求证：点在抛物线上.‎ ‎ 2．函数与直线的图象交于点，求：（1）和的值；‎ ‎ （2）求抛物线的开口方向、对称轴、顶点坐标.‎ ‎ 3．直线经过两点，它与二次函数的图象相交于两点，二次函数与的图象的开口大小和方向完全相同，并且 6‎ 的顶点坐标为，求的面积.‎ ‎【作业】‎ ‎1．抛物线的开口方向是 ，对称轴是 ，顶点坐标是 ；抛物线的对称轴是直线 ，顶点坐标是 ；‎ ‎2．在同一坐标系中，函数，，的图象的共同特点是（ ）‎ A.都是关于x轴对称，抛物线开口向上 ‎ B.都是关于y轴对称，抛物线开口向下 C.都是关于原点对称，抛物线的顶点都是原点 D.都是关于y轴对称，抛物线的顶点都是原点 ‎4．抛物线的开口向 ，对称轴是 ，顶点坐标是 ，它可以看作是由抛物线向 平移 个单位得到的．‎ ‎5．函数，当x 时，函数值y随x的增大而减小．当x 时，函数取得最 值y= ．‎ ‎6．如果将二次函数的图象沿y轴向上平移1个单位，那么所得图象的函数解析式是 .‎ ‎7．若抛物线的顶点在y轴的负半轴上，则m＝　　　　　　　．‎ ‎8．写出一个二次函数的解析式，使它的顶点恰好在直线y=x+2 上，且开口向下，你写的函数是 ‎ x A x x x y y y y B C D o o o o ‎9．在同一直角坐标系中，一次函数y＝ax＋c和二次函数y＝ax2＋c的图象大致为（ ）‎ ‎10．函数的图象与轴的交点坐标是 （ ）‎ A.（2，0） B.（，0） C.（0，4） D.（0，）‎ ‎11．一条抛物线的开口方向和对称轴都与相同，顶点纵坐标是-2，且抛物线经过点 ‎（1，1），求这条抛物线的函数关系式． ‎ 6‎