2020年云南省丽江市宁蒗县中考数学模拟试卷 解析版 21页

‎2020年云南省丽江市宁蒗县中考数学模拟试卷 一．填空题（共6小题，满分18分，每小题3分）‎ ‎1．（3分）化简：＝　 　．‎ ‎2．（3分）若+在实数范围内有意义，则实数x的取值范围是　 　．‎ ‎3．（3分）如图，在直角△ABC和直角△DBE中，∠ABC＝∠DBE＝90°，∠A＝∠D，若AB＝DB＝5，BE＝3，则CD的长为　 　．‎ ‎4．（3分）如图，在矩形ABCD中，BD是对角线，延长AD到E，使DE＝BD，连接BE．若∠EBC＝27°，则∠ABD＝　 　度．‎ ‎5．（3分）若函数y＝xm﹣1+2是一次函数，则m＝　 　．‎ ‎6．（3分）甲、乙两射击运动员的相同次数射击训练成绩的平均数和方差分别为，＝＝8，S2甲＝1.1，S2乙＝48，则成绩较为稳定的运动员是　 　．‎ 二．选择题（共8小题，满分32分，每小题4分）‎ ‎7．（4分）下列各式中，是最简二次根式的是（　　）‎ A． B． C． D．‎ ‎8．（4分）下列四组线段中，可以构成直角三角形的是（　　）‎ A．1，4，9 B．1，，2 C．1，，2 D．5，11，12‎ ‎9．（4分）如图，矩形ABCD中，AB＝8，BC＝4．点G，E分别在边AB，CD上，点F，H在对角线AC上．若四边形EFGH是菱形，则AG的长是（　　）‎ A．5 B．6 C．2 D．3‎ ‎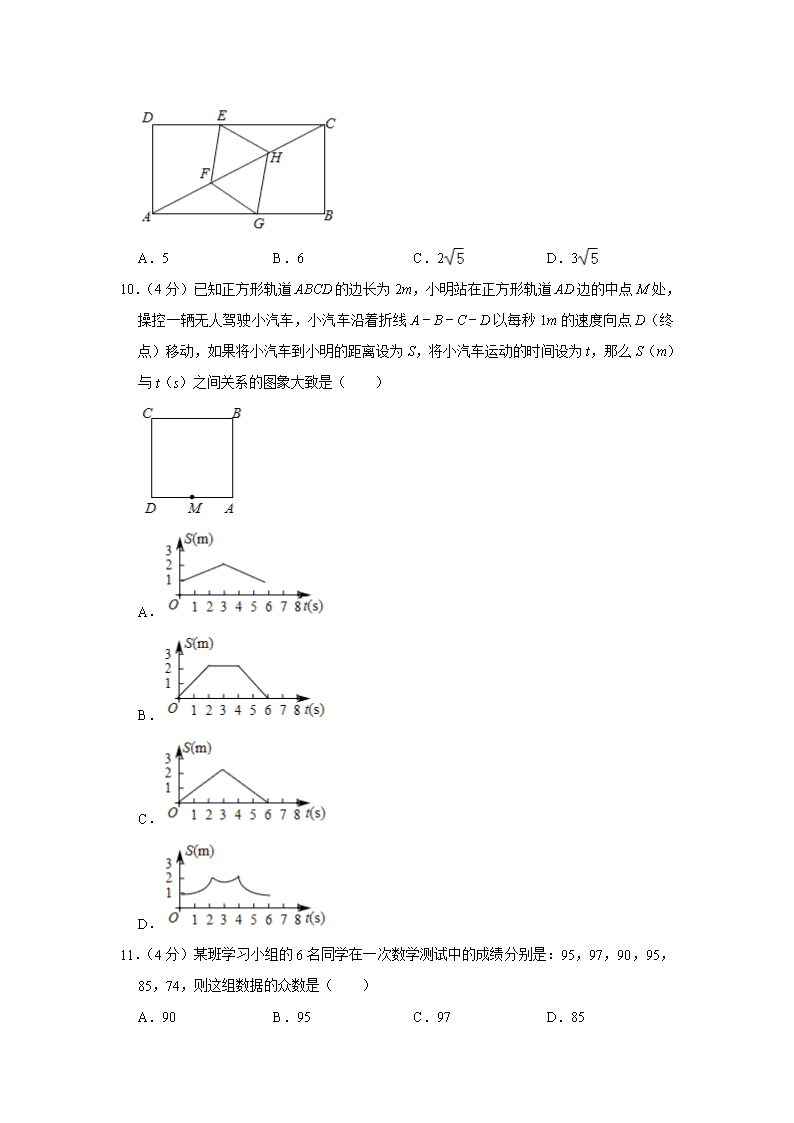10．（4分）已知正方形轨道ABCD的边长为2m，小明站在正方形轨道AD边的中点M处，操控一辆无人驾驶小汽车，小汽车沿着折线A﹣B﹣C﹣D以每秒1m的速度向点D（终点）移动，如果将小汽车到小明的距离设为S，将小汽车运动的时间设为t，那么S（m）与t（s）之间关系的图象大致是（　　）‎ A． ‎ B． ‎ C． ‎ D．‎ ‎11．（4分）某班学习小组的6名同学在一次数学测试中的成绩分别是：95，97，90，95，85，74，则这组数据的众数是（　　）‎ A．90 B．95 C．97 D．85‎ ‎12．（4分）如图，菱形ABCD的的边长为6，∠ABC＝60°，对角线BD上有两个动点E、F（点E在点F的左侧），若EF＝2，则AE+CF的最小值为（　　）‎ A．2 B．4 C．6 D．8‎ ‎13．（4分）一次函数y＝3x﹣6的图象经过（　　）‎ A．第一、二、三象限 B．第一、二、四象限 ‎ C．第二、三、四象限 D．第一、三、四象限 ‎14．（4分）下列运算正确的是（　　）‎ A．x3•x2＝x5 B．x3+x2＝x5 C．（x3）3＝x6 D．x6÷x2＝x3‎ 三．解答题（共9小题，满分70分）‎ ‎15．（5分）计算（+2）2+（+2）（﹣2）；‎ ‎16．（5分）一块木板如图所示，已知AB＝4，BC＝3，DC＝12，AD＝13，∠B＝90°，求此木板的面积．‎ ‎17．（8分）先化简，再求值：+x﹣4y﹣，其中x＝，y＝4．‎ ‎18．（9分）已知一次函数y1＝kx+b的图象经过点（﹣1，﹣3）．且与正比例函数y2＝x的图象相交于点（4，a）．‎ ‎（1）求a的值；‎ ‎（2）求一次函数y1＝kx+b的表达式；‎ ‎（3）请你画出这两个函数的图象，并判断当x取何值时，y1＞y2；‎ ‎（4）求这两个函数图象与x轴围成的三角形的面积．‎ ‎19．（8分）某蛋白粉生产厂购进了甲、乙两种包装机进行蛋白粉封装，封装的标准质量为400g．质检员对甲、乙两种包装机封装的若干蛋白粉进行了抽样调查，对数据进行分类整理分析（蛋白粉质量用x表示（单位：g），共分成四组A：390≤x＜395，B：395≤x＜400，C：400≤x＜405，D：405≤x＜410），并给出了下列信息：‎ 从甲、乙包装机封装的蛋白粉中各随机抽取10桶，测得实际质量x（单位：g）如下：‎ 甲包装机分装蛋白粉中B组的数据是：396，398，398，398．‎ 乙：400，404，396，403，400，405，397，399，400，398．‎ 甲、乙包装机封装蛋白粉的质量数据分析表 包装机器 甲 乙 平均数 ‎399.3‎ ‎400.2‎ 中位数 b ‎400‎ 众数 ‎398‎ c 方差 ‎20.4‎ ‎7.96‎ 请回答下列问题：‎ ‎（1）a＝　 　，b＝　 　，c＝　 　．‎ ‎（2）请根据以上数据判断蛋白粉包装机封装情况比较好的是　 　（填甲或乙），说明你的理由（一条理由即可）．‎ ‎（3）若甲、乙两种机器封装的这批蛋白粉各有500桶，估计这批蛋白粉的质量属于C类的数量有多少？‎ ‎20．（5分）如图，在平行四边形ABCD中，对角线AC，BD交于点O，过点O作直线EF⊥AB，分别交AB，CD于点E，F．‎ ‎（1）求证：OE＝OF；‎ ‎（2）若AC＝18，EF＝10，求AE的长．‎ ‎21．（7分）如图，小明将升旗的绳子拉到旗杆底端，并在绳子上打了一个结，然后将绳子拉到离旗杆底端9米处，发现此时绳子底端距离打结处约3米，请算出旗杆的高度．‎ ‎22．（11分）某班同学分三组进行数学活动，对七年级400名同学最喜欢喝的饮料情况，八年级300名同学零花钱的最主要用途情况，九年级300名同学完成家庭作业时间情况进行了全面调查，并分别用扇形图、频数分布直方图、表格来描述整理得到的数据．‎ 时间 ‎1小时左右 ‎1.5小时左右 ‎2小时左右 ‎2.5小时左右 人数 ‎50‎ ‎80‎ ‎120‎ ‎50‎ 根据以上信息，请回答下列问题：‎ ‎（1）七年级400名同学中最喜欢喝“冰红茶”的人数是多少；‎ ‎（2）补全八年级300名同学中零花钱的最主要用途情况频数分布直方图；‎ ‎（3）九年级300名同学中完成家庭作业的平均时间大约是多少小时？（结果保留一位小数）‎ ‎23．（12分）一块矩形纸片，利用割补的办法可以拼成一块与它面积相等的平行四边形（如图1所示）：‎ 请你根据图1作法的提示，利用图2画出一个平行四边形，使该平行四边形的面积等于所给的矩形面积．‎ 要求：（1）画出的平行四边形有且只有一个顶点与B点重合；‎ ‎（2）写出画图步骤；‎ ‎（3）写出所画的平行四边形的名称．‎ ‎2020年云南省丽江市宁蒗县中考数学模拟试卷 参考答案与试题解析 一．填空题（共6小题，满分18分，每小题3分）‎ ‎1．（3分）化简：＝　2　．‎ ‎【分析】直接利用二次根式的性质化简得出答案．‎ ‎【解答】解：＝2，‎ 故答案为：2．‎ ‎2．（3分）若+在实数范围内有意义，则实数x的取值范围是　x≥1且x≠3　．‎ ‎【分析】根据二次根式有意义的条件可得x﹣1≥0，根据分式有意义的条件可得x﹣3≠0，再解即可．‎ ‎【解答】解：由题意得：x﹣1≥0，且x﹣3≠0，‎ 解得：x≥1且x≠3，‎ 故答案为：x≥1且x≠3．‎ ‎3．（3分）如图，在直角△ABC和直角△DBE中，∠ABC＝∠DBE＝90°，∠A＝∠D，若AB＝DB＝5，BE＝3，则CD的长为　2　．‎ ‎【分析】根据全等三角形的判定与性质可求BD，再根据线段的和差关系可求CD．‎ ‎【解答】解：在Rt△ABC和Rt△DBE中，‎ ‎，‎ ‎∴Rt△ABC≌Rt△DBE（ASA），‎ ‎∴BC＝BE＝3，‎ ‎∴CD＝BD﹣BC＝5﹣3＝2．‎ 故答案为：2．‎ ‎4．（3分）如图，在矩形ABCD中，BD是对角线，延长AD到E，使DE＝BD，连接BE．若∠EBC＝27°，则∠ABD＝　36　度．‎ ‎【分析】由矩形的性质可得AD∥BC，∠ABC＝90°，由平行线的性质和等腰三角形的性质可得∠EBC＝∠DBE＝∠E＝27°，即可求解．‎ ‎【解答】解：∵四边形ABCD是矩形，‎ ‎∴AD∥BC，∠ABC＝90°，‎ ‎∴∠EBC＝∠E＝27°，‎ ‎∵DE＝BD，‎ ‎∴∠DBE＝∠E＝27°，‎ ‎∴∠ABD＝∠ABC﹣∠DBE﹣∠EBC＝36°，‎ 故答案为：36．‎ ‎5．（3分）若函数y＝xm﹣1+2是一次函数，则m＝　2　．‎ ‎【分析】依据一次函数的定义可得到关于m的方程，从而可求得m的值．‎ ‎【解答】解：由题意得，m﹣1＝1，‎ 解得m＝2．‎ 故答案为：2．‎ ‎6．（3分）甲、乙两射击运动员的相同次数射击训练成绩的平均数和方差分别为，＝＝8，S2甲＝1.1，S2乙＝48，则成绩较为稳定的运动员是　甲　．‎ ‎【分析】方差越小成绩越稳定，据此可得答案．‎ ‎【解答】解：∵S2甲＝1.1，S2乙＝48，‎ ‎∴S2甲＜S2乙，‎ ‎∴成绩较为稳定的运动员是甲，‎ 故答案为：甲．‎ 二．选择题（共8小题，满分32分，每小题4分）‎ ‎7．（4分）下列各式中，是最简二次根式的是（　　）‎ A． B． C． D．‎ ‎【分析】利用最简二次根式定义判断即可．‎ ‎【解答】解：A.，故本选项不合题意；‎ B.，故本选项不合题意；‎ C.是最简二次根式，故本选项符合题意；‎ D.，故本选项不合题意．‎ 故选：C．‎ ‎8．（4分）下列四组线段中，可以构成直角三角形的是（　　）‎ A．1，4，9 B．1，，2 C．1，，2 D．5，11，12‎ ‎【分析】根据勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个是直角三角形判定则可．如果有这种关系，这个就是直角三角形．‎ ‎【解答】解：A、∵12+42≠92，∴该三角形不符合勾股定理的逆定理，故不可以构成直角三角形；‎ B、∵12+（）2≠22，∴该三角形不符合勾股定理的逆定理，故不可以构成直角三角形；‎ C、∵12+（）2＝22，∴该三角形符合勾股定理的逆定理，故可以构成直角三角形；‎ D、∵52+112≠122，∴该三角形不符合勾股定理的逆定理，故不可以构成直角三角形．‎ 故选：C．‎ ‎9．（4分）如图，矩形ABCD中，AB＝8，BC＝4．点G，E分别在边AB，CD上，点F，H在对角线AC上．若四边形EFGH是菱形，则AG的长是（　　）‎ A．5 B．6 C．2 D．3‎ ‎【分析】连接EG交AC于O，易证得△CEO≌△AOG（AAS），可得OA＝OC，由勾股定理求得AC的长，求得OA的长，证△AOG∽△ABC，利用相似三角形的对应边成比例，即可求得答案．‎ ‎【解答】解：连接GE交AC于O，如图：‎ ‎∵四边形EFGH是菱形，‎ ‎∴GE⊥AC，OG＝OE，‎ ‎∵四边形ABCD是矩形，‎ ‎∴∠B＝∠D＝90°，AB∥CD，‎ ‎∴∠ACD＝∠CAB，‎ 在△CEO与△AOG中，，‎ ‎∴△CEO≌△AOG（AAS），‎ ‎∴AO＝CO，‎ ‎∵AC＝＝＝4，‎ ‎∴AO＝AC＝2，‎ ‎∵∠CAB＝∠CAB，∠AOG＝∠B＝90°，‎ ‎∴△AOG∽△ABC，‎ ‎∴＝，‎ 即＝，‎ ‎∴AG＝5；‎ 故选：A．‎ ‎10．（4分）已知正方形轨道ABCD的边长为2m，小明站在正方形轨道AD边的中点M处，操控一辆无人驾驶小汽车，小汽车沿着折线A﹣B﹣C﹣D以每秒1m的速度向点D（终点）移动，如果将小汽车到小明的距离设为S，将小汽车运动的时间设为t，那么S（m）与t（s）之间关系的图象大致是（　　）‎ A． ‎ B． ‎ C． ‎ D．‎ ‎【分析】求出小汽车在AB、BC上运动时，MQ的表达式即可求解．‎ ‎【解答】解：设小汽车所在的点为点Q，‎ ‎①当点Q在AB上运动时，AQ＝t，‎ 则MQ2＝MA2+AQ2＝1+t2，‎ 即MQ2为开口向上的抛物线，则MQ为曲线，‎ ‎②当点Q在BC上运动时，‎ 同理可得：MQ2＝22+（1﹣t+2）2＝4+（3﹣t）2，‎ MQ为曲线；‎ 故选：D．‎ ‎11．（4分）某班学习小组的6名同学在一次数学测试中的成绩分别是：95，97，90，95，85，74，则这组数据的众数是（　　）‎ A．90 B．95 C．97 D．85‎ ‎【分析】直接根据众数的概念求解可得．‎ ‎【解答】解：这组数据中出现次数最多的是95，出现2次，‎ 所以这组数据的众数为95，‎ 故选：B．‎ ‎12．（4分）如图，菱形ABCD的的边长为6，∠ABC＝60°，对角线BD上有两个动点E、F（点E在点F的左侧），若EF＝2，则AE+CF的最小值为（　　）‎ A．2 B．4 C．6 D．8‎ ‎【分析】作AM⊥AC，连接CM交BD于F，根据菱形的性质和等边三角形的判定和性质以及勾股定理解答即可．‎ ‎【解答】解：如图，连接AC，作AM⊥AC，使得AM＝EF＝2，连接CM交BD于F，‎ ‎∵AC，BD是菱形ABCD的对角线，‎ ‎∴BD⊥AC，‎ ‎∵AM⊥AC，‎ ‎∴AM∥BD，‎ ‎∴AM∥EF，‎ ‎∵AM＝EF，AM∥EF，‎ ‎∴四边形AEFM是平行四边形，‎ ‎∴AE＝FM，‎ ‎∴AE+CF＝FM+FC＝CM，‎ 根据两点之间线段最短可知，此时AE+FC最短，‎ ‎∵四边形ABCD是菱形，AB＝6，∠ABC＝60°‎ ‎∴BC＝AB，‎ ‎∴△ABC是等边三角形，‎ ‎∴AC＝AB＝6，‎ 在Rt△CAM中，CM＝＝‎ ‎∴AE+CF的最小值为2．‎ 故选：A．‎ ‎13．（4分）一次函数y＝3x﹣6的图象经过（　　）‎ A．第一、二、三象限 B．第一、二、四象限 ‎ C．第二、三、四象限 D．第一、三、四象限 ‎【分析】根据题目中的函数解析式和一次函数的性质，可以判断该函数图象经过哪几个象限．‎ ‎【解答】解：∵一次函数y＝3x﹣6，‎ ‎∴该函数的图象经过第一、三、四象限，‎ 故选：D．‎ ‎14．（4分）下列运算正确的是（　　）‎ A．x3•x2＝x5 B．x3+x2＝x5 C．（x3）3＝x6 D．x6÷x2＝x3‎ ‎【分析】分别根据同底数幂的乘法法则，合并同类项法则，幂的乘方运算法则以及同底数幂的除法法则逐一判断即可．‎ ‎【解答】解：A．x3•x2＝x5，故本选项符合题意；‎ B．x3与x2不是同类项，所以不能合并，故本选项不合题意；‎ C．（x3）3＝x9，故本选项不合题意；‎ D．x6÷x2＝x4，故本选项不合题意．‎ 故选：A．‎ 三．解答题（共9小题，满分70分）‎ ‎15．（5分）计算（+2）2+（+2）（﹣2）；‎ ‎【分析】直接利用乘法公式计算得出答案．‎ ‎【解答】解：（+2）2+（+2）（﹣2）‎ ‎＝5+4+4+5﹣4‎ ‎＝10+4．‎ ‎16．（5分）一块木板如图所示，已知AB＝4，BC＝3，DC＝12，AD＝13，∠B＝90°‎ ‎，求此木板的面积．‎ ‎【分析】连接AC，利用勾股定理解出直角三角形ABC的斜边，通过三角形ACD的三边关系可确定它为直角三角形，木板面积为这两三角形面积之差．‎ ‎【解答】解：连接AC，‎ ‎∵在△ABC中，AB＝4，BC＝3，∠B＝90°，‎ ‎∴AC＝5，‎ ‎∵在△ACD中，AC＝5，DC＝12，AD＝13，‎ ‎∴DC2+AC2＝122+52＝169，AD2＝132＝169，‎ ‎∴DC2+AC2＝AD2，‎ ‎∴△ACD为直角三角形，AD为斜边，‎ ‎∴木板的面积为：S△ACD﹣S△ABC＝×5×12﹣×3×4＝24．‎ 答：此木板的面积为24．‎ ‎17．（8分）先化简，再求值：+x﹣4y﹣，其中x＝，y＝4．‎ ‎【分析】直接利用二次根式的性质化简，进而把已知数据代入得出答案．‎ ‎【解答】解：原式＝5+x•﹣4y•﹣•y ‎＝5+﹣4﹣‎ ‎＝，‎ 当x＝，y＝4时，‎ 原式＝＝．‎ ‎18．（9分）已知一次函数y1＝kx+b的图象经过点（﹣1，﹣3）．且与正比例函数y2＝x的图象相交于点（4，a）．‎ ‎（1）求a的值；‎ ‎（2）求一次函数y1＝kx+b的表达式；‎ ‎（3）请你画出这两个函数的图象，并判断当x取何值时，y1＞y2；‎ ‎（4）求这两个函数图象与x轴围成的三角形的面积．‎ ‎【分析】（1）将点（4，a）代入正比例函数y2＝x即可求出a的值；‎ ‎（2）根据（1）所求，及一次函数y＝kx+b的图象经过两点（﹣1，﹣3）、（4，2），用待定系数法可求出函数关系式；‎ ‎（3）根据两点确定一直线画出这两个函数的图象，观察函数图象得到当x＞4时，一次函数y1＝kx+b的图象在正比例函数y2＝x的图象的上方，即y1＞y2；‎ ‎（4）先确定一次函数与x轴的交点坐标，然后根据三角形面积公式求解．‎ ‎【解答】解：（1）∵正比例函数y2＝x的图象过点（4，a），‎ ‎∴a＝×4＝2；‎ ‎（2）∵一次函数y1＝kx+b的图象经过两点（﹣1，﹣3）、（4，2），‎ ‎∴，解得，‎ ‎∴y＝x﹣2．‎ 故所求一次函数的解析式为y1＝x﹣2；‎ ‎（3）函数图象如图：‎ 由图象可知，当x＞4时，y1＞y2；‎ ‎（4）一次函数的表达式为：y1＝x﹣2，与x轴交于（2，0），‎ ‎∵正比例函数y＝x与一次函数y＝x﹣2的交点为（4，2），‎ ‎∴两个函数图象与x轴所围成的三角形面积为×2×2＝2．‎ ‎19．（8分）某蛋白粉生产厂购进了甲、乙两种包装机进行蛋白粉封装，封装的标准质量为400g．质检员对甲、乙两种包装机封装的若干蛋白粉进行了抽样调查，对数据进行分类整理分析（蛋白粉质量用x表示（单位：g），共分成四组A：390≤x＜395，B：395≤x＜400，C：400≤x＜405，D：405≤x＜410），并给出了下列信息：‎ 从甲、乙包装机封装的蛋白粉中各随机抽取10桶，测得实际质量x（单位：g）如下：‎ 甲包装机分装蛋白粉中B组的数据是：396，398，398，398．‎ 乙：400，404，396，403，400，405，397，399，400，398．‎ 甲、乙包装机封装蛋白粉的质量数据分析表 包装机器 甲 乙 平均数 ‎399.3‎ ‎400.2‎ 中位数 b ‎400‎ 众数 ‎398‎ c 方差 ‎20.4‎ ‎7.96‎ 请回答下列问题：‎ ‎（1）a＝　40　，b＝　398　，c＝　400　．‎ ‎（2）请根据以上数据判断蛋白粉包装机封装情况比较好的是　乙　（填甲或乙），说明你的理由（一条理由即可）．‎ ‎（3）若甲、乙两种机器封装的这批蛋白粉各有500桶，估计这批蛋白粉的质量属于C类的数量有多少？‎ ‎【分析】（1）甲包装机分装奶粉中B组的数据个数除以10得到a的值，利用中位数的定义，找出甲包装机分装奶粉中的数据中的第5个和第6个数即可得到b的值，利用众数的定义确定c的值；‎ ‎（2）利用方差和众数的意义进行判断；‎ ‎（3）用500分别乘以甲、乙包装机分装奶粉中C组数据的个数所占的百分比即可．‎ ‎【解答】解：（1）a%＝×100%＝40%，即a＝40，‎ 甲包装机分装奶粉中A组的数据有10×20%＝2（个），‎ 所以甲包装机分装奶粉中的数据中的第5个和第6个数都是398，所以b＝398；‎ 乙包装机分装奶粉中的数据的众数为400，即c＝400；‎ 故答案为：40、398、400；‎ ‎（2）奶粉包装机封装情况比较好的是乙．‎ 理由如下：乙的方差小，比较稳定；‎ 故答案为：乙；‎ ‎（3）500×30%+500×＝400，‎ 所以这批奶粉的质量属于C类的数量有400桶．‎ ‎20．（5分）如图，在平行四边形ABCD中，对角线AC，BD交于点O，过点O作直线EF⊥AB，分别交AB，CD于点E，F．‎ ‎（1）求证：OE＝OF；‎ ‎（2）若AC＝18，EF＝10，求AE的长．‎ ‎【分析】（1）根据平行四边形的性质得出AB∥CD，OA＝OC，利用全等三角形的判定和性质解答即可；‎ ‎（2）根据平行四边形的性质和勾股定理解答即可．‎ ‎【解答】证明：（1）∵四边形ABCD是平行四边形，‎ ‎∴AB∥CD，OA＝OC，‎ ‎∴∠FCO＝∠OAE，‎ ‎∵EF⊥AB，‎ ‎∴EF⊥CD，‎ ‎∴∠CFO＝∠AEO＝90°，‎ ‎∴△FCO≌△EAO（AAS），‎ ‎∴OE＝OF；‎ ‎（2）∵四边形ABCD是平行四边形，‎ ‎∴OA＝OC＝9，‎ ‎∵OE＝OF，‎ ‎∴OE＝5，‎ ‎∴AE＝．‎ ‎21．（7分）如图，小明将升旗的绳子拉到旗杆底端，并在绳子上打了一个结，然后将绳子拉到离旗杆底端9米处，发现此时绳子底端距离打结处约3米，请算出旗杆的高度．‎ ‎【分析】设旗杆的高度为x米，由勾股定理得出方程，解方程即可．‎ ‎【解答】解：设旗杆的高度为x米，‎ 根据勾股定理，得x2+92＝（x+3）2，‎ 解得：x＝12；‎ 答：旗杆的高度为12米 ‎22．（11分）某班同学分三组进行数学活动，对七年级400名同学最喜欢喝的饮料情况，八年级300名同学零花钱的最主要用途情况，九年级300名同学完成家庭作业时间情况进行了全面调查，并分别用扇形图、频数分布直方图、表格来描述整理得到的数据．‎ 时间 ‎1小时左右 ‎1.5小时左右 ‎2小时左右 ‎2.5小时左右 人数 ‎50‎ ‎80‎ ‎120‎ ‎50‎ 根据以上信息，请回答下列问题：‎ ‎（1）七年级400名同学中最喜欢喝“冰红茶”的人数是多少；‎ ‎（2）补全八年级300名同学中零花钱的最主要用途情况频数分布直方图；‎ ‎（3）九年级300名同学中完成家庭作业的平均时间大约是多少小时？（结果保留一位小数）‎ ‎【分析】（1）先求出喝红茶的百分比，再乘总数．‎ ‎（2）先让总数减其它三种人数，再根据数值画直方图．‎ ‎（3）用加权平均公式求即可．‎ ‎【解答】解：（1）冰红茶的百分比为100%﹣25%﹣25%﹣10%＝40%，冰红茶的人数为400×40%＝160（人），‎ 即七年级同学最喜欢喝“冰红茶”的人数是160人；‎ ‎（2）补全频数分布直方图如右图所示．‎ ‎（3）（小时）．‎ 答：九年级300名同学完成家庭作业的平均时间约为1.8小时．‎ ‎23．（12分）一块矩形纸片，利用割补的办法可以拼成一块与它面积相等的平行四边形（如图1所示）：‎ 请你根据图1作法的提示，利用图2画出一个平行四边形，使该平行四边形的面积等于所给的矩形面积．‎ 要求：（1）画出的平行四边形有且只有一个顶点与B点重合；‎ ‎（2）写出画图步骤；‎ ‎（3）写出所画的平行四边形的名称．‎ ‎【分析】根据平行四边形及矩形的性质，结合题意要求作出图形即可，注意语言的规范性．‎ ‎【解答】解：作图：如图所示 ‎（1）过点C作射线CE（不过A、D点）；‎ ‎（2）过点B作射线BF∥CE，且交DA的延长线于点F；‎ ‎（3）在CE上任取一点G，连接BG；‎ ‎（4）过点F作FE∥BG，交射线CE于点E，‎ 则四边形BGEF为所画的平行四边形．‎