五年级下册数学教案 4 表面积的变化 沪教版 (1) 6页

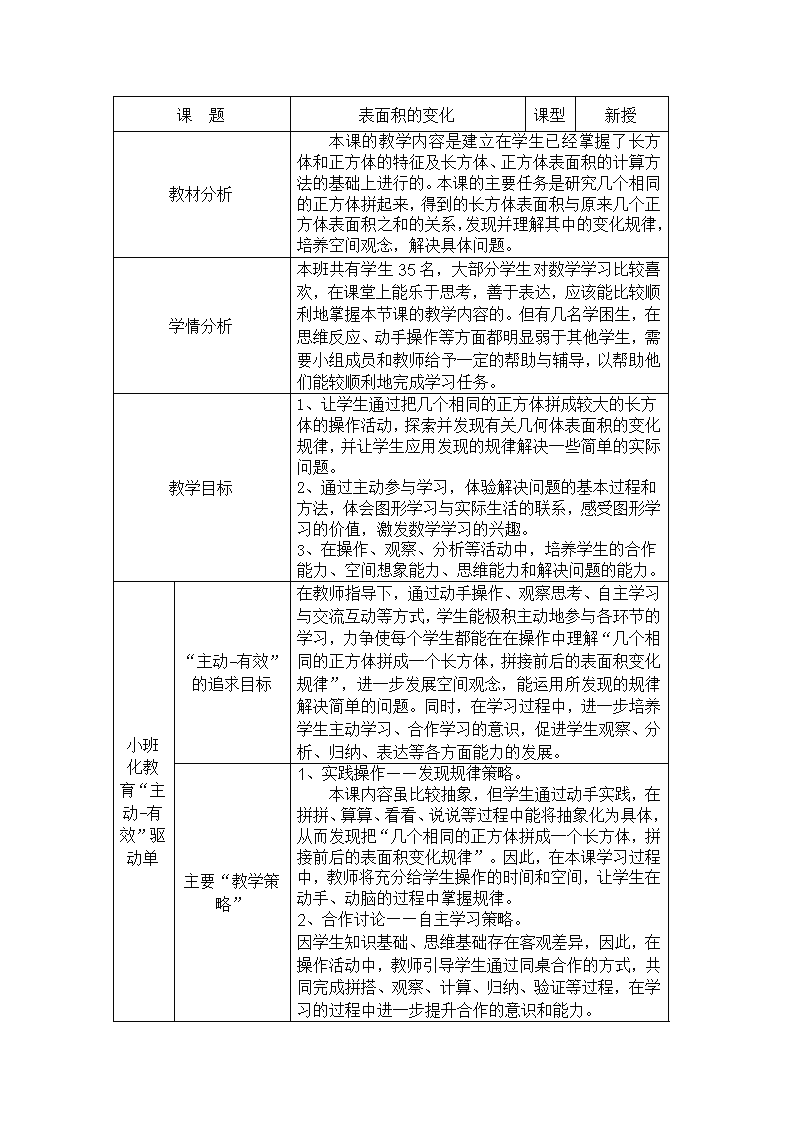
课 题 表面积的变化 课型 新授 教材分析 本课的教学内容是建立在学生已经掌握了长方 体和正方体的特征及长方体、正方体表面积的计算方 法的基础上进行的。本课的主要任务是研究几个相同 的正方体拼起来，得到的长方体表面积与原来几个正 方体表面积之和的关系，发现并理解其中的变化规 律，培养空间观念，解决具体问题。 学情分析 本班共有学生 35 名，大部分学生对数学学习比较喜 欢，在课堂上能乐于思考，善于表达，应该能比较顺 利地掌握本节课的教学内容的。但有几名学困生，在 思维反应、动手操作等方面都明显弱于其他学生，需 要小组成员和教师给予一定的帮助与辅导，以帮助他 们能较顺利地完成学习任务。 教学目标 1、让学生通过把几个相同的正方体拼成较大的长方 体的操作活动，探索并发现有关几何体表面积的变化 规律，并让学生应用发现的规律解决一些简单的实际 问题。 2、通过主动参与学习，体验解决问题的基本过程和 方法，体会图形学习与实际生活的联系，感受图形学 习的价值，激发数学学习的兴趣。 3、在操作、观察、分析等活动中，培养学生的合作 能力、空间想象能力、思维能力和解决问题的能力。 小班 化教 育“主 动-有 效”驱 动单 “主动-有效” 的追求目标 在教师指导下，通过动手操作、观察思考、自主学习 与交流互动等方式，学生能极积主动地参与各环节的 学习，力争使每个学生都能在在操作中理解“几个相 同的正方体拼成一个长方体，拼接前后的表面积变化 规律”，进一步发展空间观念，能运用所发现的规律 解决简单的问题。同时，在学习过程中，进一步培养 学生主动学习、合作学习的意识，促进学生观察、分 析、归纳、表达等各方面能力的发展。 主要“教学策 略” 1、实践操作——发现规律策略。 本课内容虽比较抽象，但学生通过动手实践，在 拼拼、算算、看看、说说等过程中能将抽象化为具体， 从而发现把“几个相同的正方体拼成一个长方体，拼 接前后的表面积变化规律”。因此，在本课学习过程 中，教师将充分给学生操作的时间和空间，让学生在 动手、动脑的过程中掌握规律。 2、合作讨论——自主学习策略。 因学生知识基础、思维基础存在客观差异，因此，在 操作活动中，教师引导学生通过同桌合作的方式，共 同完成拼搭、观察、计算、归纳、验证等过程，在学 习的过程中进一步提升合作的意识和能力。 教学重点、教学难点 探索多个相同正方体叠放后表面积的变化规律，在探 索活动中培养空间想象能力和解决实际问题的能力 等。 课前准备 1、以四人小组为单位，每小组准备 6 个 1 立方 厘米的正方体。明确分工：摆（组长）、看（四人）、 议（四人）、填（一组员）。 2、课堂练习卷。 3、多媒体课件 教学 环节 教 学 过 程 教 师 活 动 学生活动 设计意图 一、 复习 引入 二、 1、口答： 正方体体积怎么计算？（文字、字母） V 正=a3 表面积呢？（文字、字母） S 正=6a2 2、棱长为 1cm 的小正方体，他的体 积是多少？ 多媒体演示： 这里有 2 个棱长为 1cm 的小正方体， 他们的体积和是？ 现在将这2个棱长为1cm的小正方体 拼成一个长方体，体积有没有变化？ （横的、竖的都演示一下） 这里有 3 个棱长为 1cm 的小正方体， 他们的体积和是？ 现在将这3个棱长为1cm的小正方体 拼成一个长方体，体积有没有变化？ 4 个呢？5 个呢？…… 小结：我们已经知道，物体的体积不 因形状的改变、分拆或组合而发生变 化。（教师可补充演示一些通过形状 的改变使组合是不规则图形的例子） 那么新拼成的长方体的表面积与原 来正方体的表面积之和是否相等 呢？ 1、棱长为 1cm 的小正方体，一个面 学生口答 学 生 按要 求 计 算并回答 【复习长方体、 正方体表面积 和体积的计算 方法，为今天的 探 究 做 好 准 备。】 探究 的面积是多少？他的表面积呢？ 多媒体出示： 这里有 2 个棱长为 1cm 的小正方体， 他们的表面积和是？ 现在将这2个棱长为1cm的小正方体 拼成一个长方体，（横的、竖的都演 示一下）表面积是多少？计算一下。 有没有变化？ 反馈小结：小正方体拼接以后，表面 积发生了变化。板示：表面积的变化 2、老师告诉你们这变化是有规律的， 规律是什么呢？ 出示表格： 我们来动手拼一拼，把小正方体摆成 一行拼成一个长方体,然后填一填，想 一想。 拼的正方 体的个数 2 3 4 5 6 原来正方 体的表面 积之和 （cm2） 12 拼成后的 长方体的 表面积 （cm2） 10 减少的面 积（cm2） 2 重叠的次 数（次） 1 减少了原 来正方体 几个面的 面积（个） 2 用 自 己喜 欢 的 方 法 计算 重 组 后 的 长方 体 的 表 面 积并 发 现 变化。 学 生 独立 按 要 求动手拼一拼。 完成表格。思考 变化规律。 小 组 合作 交 流 讨论：表面积的 变 化 规律 是 什 么？ 集体交流小结。 A、两个正方体 拼 成 一个 长 方 体后，表面积减 少 了 原来 2 个 正 方 形面 的 面 积。 （小结板书：重 叠 1 次，减少 2 个面） B、拼成的长方 体 的 表面 积 比 原 来 两个 正 方 体 的 表面 积 之 和 减 少了 2 平 方厘米。 C、3 个小正方 体 拼 成一 个 长 方体后，它的表 面 积 减少 了 原 来 正 方体 4 个 通过初次操作， 发现存在这样 一个现象：两个 正方体拼成一 个长方体后，体 积不变，表面积 减 少 了 原 来 2 个正方形面的 面积。】 三、 运用 3、谁来总结一下表面积的变化规 律？ 将几个棱长为 1cm 的小正方体摆成 一行拼成一个长方体，表面积与原来 小正方体的表面积之和比，发生了变 化。每重叠一次，就减少两个面。（修 正板书： 每重叠一次，就减少两个面。 摆一行时： 重叠的次数=小正方体个数-1 减少的面的个数 =重叠次数×2） （一）基本题 1、猜想： 将 7 个体积为 1cm3 的小正方体摆成 一行，拼成一个长方体，表面积比原 来小正方体的表面积之和减少了多 少平方厘米？（猜后自己动手验证）。 2、P61 试一试。 （注意：3 个正方体拼成一个长方体， 减少了 4 个正方形的面，而一个正方 形的面的面积是 4 cm2，所以表面积 面的面积。（小 结板书：重叠 2 次 ， 减 少 4 个 面） D、4 个、5 个、 6 个个小正方体 拼 成 一个 长 方 体后，它的表面 积 减 少了 原 来 正方体 6 个、8 个、10 个面的 面积。（小结板 书：重叠 3 次， 减少 6 个面 重叠 4 次，减少 8 个面 重叠 5 次，减少 10 个面） 学 生 尝试 总 结 表 面 积的 变 化 规律。 【通过几次操 作，让学生经历 探究的过程，使 他们体会：不仅 仅是 2 个小正 方体拼成一个 长方体后有这 样的现象，若干 个小正方体拼 成一个长方体 后都存在这样 的现象。】 【尝试归纳结 论，帮助理解和 记忆。】 1 3 1 比原来小正方体的表面积之和减少 了 4×4=16 cm2。） 3、思考： 将下图切割成 3 个体积为 1cm3 的小 正方体，这 3 个小正方体的表面积之 和与原来长方体比，结果怎样？ （二）拓展 1、有 4 个体积为 1 cm3 的小正方体， 小胖搭成了下面几个不同的立体形 状，它们的表面积相等吗？为什么？ 什么情况下，搭成的立体形状的表面 积相等？ 2、将 27 个棱长为 1cm 的小正方体拼 搭成一个棱长为 3cm 大正方体，如果 要拿走其中的一个小正方体，剩下的 立体形状的表面积与原来大正方体 练 习 巩固 并 拓 展延伸。 【培养学生能 灵活运用规律， 解决问题的能 力。】 【通过练习，使 学生体会：若干 个相同的小正 方体拼成不同 形状的立体形 状，只要重叠面 的个数相同，表 面积就相等。】 【通过练习，使 学生体会：在不 同的位置上取 小正方体，表面 四、 总结 的表面积比，会有什么变化？（提示： 可以在不同的位置上取这个小正方 体。） 今天我们学习了什么？通过今天的 学习，你有哪些收获？ 附板书设计： 表面积的变化 每重叠一次，减少两个面。 摆一行时： 重叠的次数=小正方体个数-1 减少的面的个数 =重叠次数×2 积的变化不相 同。】