- 228.00 KB
- 2021-12-23 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
三角形三边的关系
教学目标:
1. 通过观察、操作、实验等活动,探索并发现 “三角形两边之和大于第三
边”这一规律。
2. 经历探究过程,培养学生自主探究、合作交流的能力
3. 在学习的过程中体会数学知识之间的的密切联系,培养合作意识和探索精
神,养成善于观察、勤于思考的良好学习习惯。
教学重点:
理解并掌握三角形三边的关系。
教学难点:
应用三角形三边的关系解决问题。
教学过程:
一、 导入
线段公理
在 A、B 两个点之间,我们连了若干条线,认真观察,哪一条连线最短?它
有什么特点?
教师总结:两点之间的连线,线段最短。
二、 探究新知
利用课件隐去多余的连线,只剩下下面这幅图。
①
②
④
⑤⑤
②
③ ③
④
A B
师:根据刚才讨论,我们知道从 A 点到 B 点的连线中,上面两条线段长度的和一
定大于下面的线段,所以 a+b>c。
2.三角形三边的关系。
(1)师:这两条连线组成我们学过的什么图形?那么我们可以把刚才找最短连
线的问题,转化成研究三角形三条边的长度问题。
师:通过比较两种路线的长度,你发现三角形三边之间有怎样的关系?
(2)揭示规律的必要性。[结合学生发言,板书:三角形两边之和大于第三边。]
(3)揭示规律的充分性。
师:还有别的两边之和大于第三边的情况吗?
同桌讨论,得出结论:a+c>b , c +b>a 。
师:刚才的探究结果,是基于老师屏幕上的三角形得出来的,那其他三角形
是否也有这个结果呢?
学生验证自己画的三角形三条边是否有这个结论。
师:我们一起验证了多个不同的三角形,都有这个结果,所以三角形两边之和大
于第三边。既然无论选哪两边的和与第三边比较,都得到这个结果,那么你认为
这个结论应该补充一个什么词呢?为什么要加这个词?这个词有什么含义?
[板书修正结论:三角形任意两边之和大于第三边]
三、 实验:探究围成三角形的条件
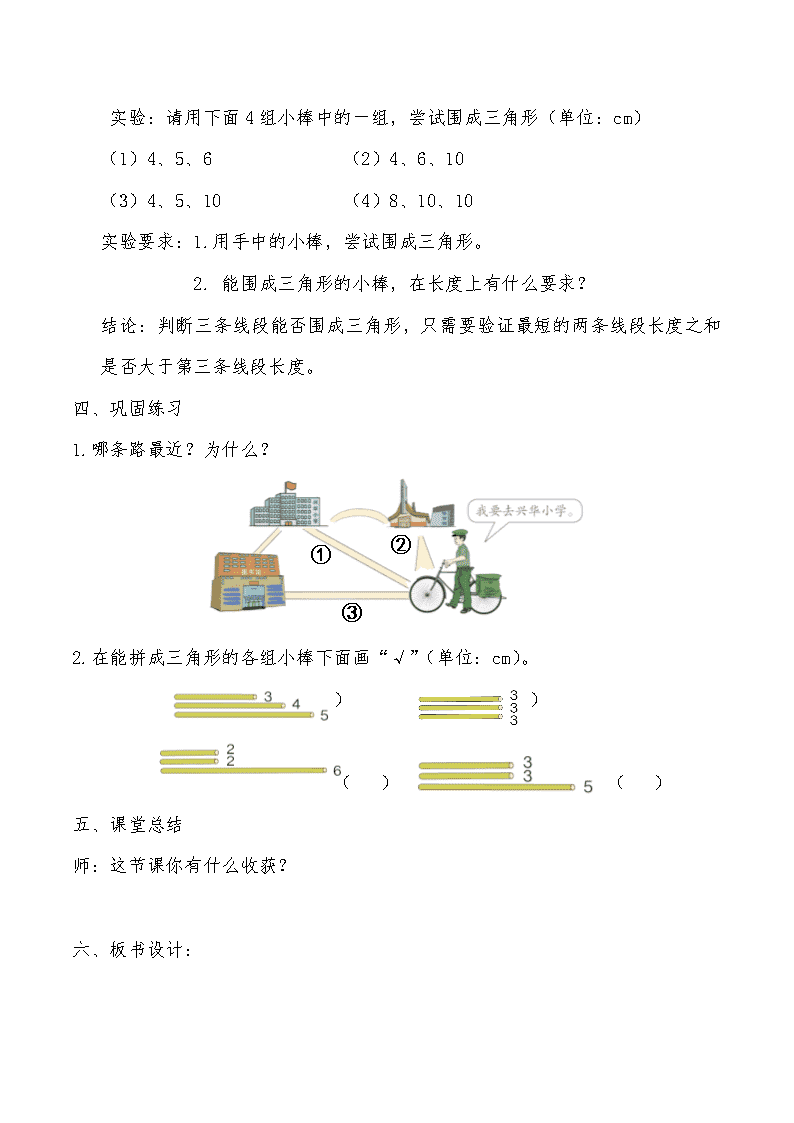
实验:请用下面 4 组小棒中的一组,尝试围成三角形(单位:cm)
C
A B
(1)4、5、6 (2)4、6、10
(3)4、5、10 (4)8、10、10
实验要求:1.用手中的小棒,尝试围成三角形。
2. 能围成三角形的小棒,在长度上有什么要求?
结论:判断三条线段能否围成三角形,只需要验证最短的两条线段长度之和
是否大于第三条线段长度。
四、巩固练习
1.哪条路最近?为什么?
2.在能拼成三角形的各组小棒下面画“√”(单位:cm)。
( ) ( )
( ) ( )
五、课堂总结
师:这节课你有什么收获?
六、板书设计:
√
(
(
((
① ②
③
任意两条线段的和大于第三条线段
C
A B
三角形的三边不等关系
两点之间的连线,线段最短
三角形任意两边之和大于第三边
a+b>c a+c>b b+c>a