人教版六年级下册数学教材分析 102页

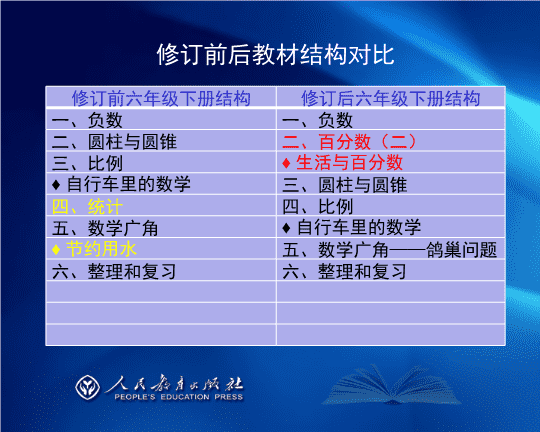
义务教育教科书 数学 六年级下册 教材介绍 小学数学室 修订前六 年级 下 册 结构 修订后六 年级 下 册 结构 一、负数 一、负数 二、圆柱与圆锥 二、百分数（二） 三、比例 ♦ 生活与百分数 ♦ 自行车里的数学 三、圆柱与圆锥 四、统计 四、比例 五、数学广角 ♦ 自行车里的数学 ♦ 节约用水 五、数学广角 —— 鸽巢问题 六、整理和复习 六、整理和复习 修订前后教材结构对比 第一单元 负数 一、教学内容 认识生活中的正、负数 课标要求 在熟悉的生活情境中，了解负数的意义，会用负数表示日常生活中的一些量。 二、与实验教材的主要区别 例 1 情境更加丰富，增加了学生理解正、负数意义的机会。 删去了正数、 0 、负数比较大小的内容。 更加强调结合具体的量认识正、负数的现实含义。 不再使用“数轴”这一名词。 三、具体编排 温度中的负数 收支中的负数 例 1 数轴上的负数 例 3 负数 例 2 实验教材 修订教材 支出 存入 利息 结余 300.00 1200.00 500.00 1700.00 12.35 1712.35 中国银行活期存折 符号、绝对值 一上 三下 五上 四、教学中需注意的问题 1 ．在具体生活情境中认识负数。 温度、收支、相对水位、海拔、时区、误差、负增长 …… 2 ． 结合现实素材对正、负号所表示的不同含 义加以区分 。 温度是 +2℃ ，温度是 -2℃ 。 温度上升 2℃ 用 +2℃ 表示，下降 2℃ 用 -2℃ 表示。 数轴上原点左边某点用 -1 表示，右边某点用 1 表示。 向东走 1m 用 +1m 表示，向右走 1m 用 -1m 表示。 顺时针、逆时针的角度表示。 25º -25º 3 ．把握好教学 要求 。 实验教材 第二单元 百分数（二） 一、教学内容 折扣 成数 税率 利率 二、与实验教材的主要区别 把实验教材六年级上册的百分数分成两段，把有关百分数的具体应用移至本册。 “成数”的内容由“你知道吗”变成正式教学内容。 新编了“购物中的实际问题”。 两段“百分数”的侧重点不同 六年级上册：百分数意义的理解、把分数相应数量关系迁移类推到百分数来解决一般性的百分数实际问题。 六年级下册：理解四类特殊百分数的现实含义，除了掌握一般性的数量关系以外，更需要学生 理解很多“数学之外”的知识，如税务知识、金融知识等 。 三、具体编排 折扣 成数 例 1 税率 例 3 百分数（二） 例 2 利率 例 4 解决实际问题 例 5 打七折 ——OFF 70% 三个变量 利率与存期的对应性 还有各种复杂的情形 不计算，知道哪个商场的折扣多吗？ 在 B 商场，相当于打了几折？ 什么时候两个商场折扣差别最小？什么时候差别最大？ 四、教学中需注意的问题 1 ．加强数学与实际生活的联系，培养学生应用数学的意识。 2 ．开放教学过程，培养学生综合应用数学的能力。 第三单元 圆柱与圆锥 一、教学内容 1. 圆柱 圆柱的认识 圆柱的表面积 圆柱的体积 2. 圆锥 圆锥的认识 圆锥的体积 二、与实验教材的主要区别 新编了一道“解决实际问题”的例题。 三、具体编排 圆柱与圆锥 圆柱 圆锥 圆柱的认识 例 1 、例 2 圆柱的表面积 例 3 、例 4 圆柱的体积 例 5 ～ 例 7 圆锥的认识 圆锥的体积 例 1 例 2 、例 3 r d=r d≤r r d=r d≤r d=r d≤r d=r d≤r 实际情境中表面积包括哪些部分？ 计算器的使用 积分的思想 基础知识：容积的概念、圆柱体积计算 基本技能：测量、计算等 基本思想：转化的思想、变中有不变的思想 基本活动经验：问题意识的培养、问题解决策略的培养 如何在本例教学中体现四基、四能？ 这是一个非常规问题，不是简单套用公式就可解决 发现问题 提出问题 分析问题 解决问题 环节一： 教师直接出示一个空的矿泉水瓶，提问：这个矿泉水瓶的容积是多少？ （ 学生可能无处 着 手，也可能会通过寻找标签上的“净含量”来代替矿泉水瓶的容积。 ） 教师可在肯定学生思路的基础上，引导学生回顾容积的概念，并找到解决问题的方向：假如瓶子里灌满了水，把这些水倒出来，用量杯或量筒测出水的体积就可以求出瓶子的容积。 环节二： 教师进一步提出要求 ： 要是没有这些工具，甚至连一个玻璃杯都没有，只提供水和直尺，怎么办？ 通过出示存了一部分水的瓶子，引导学生思考：此时瓶子的容积可由哪两部分组成？使学生观察到瓶子的容积由水的体积和空气的体积两部分组成，其中水的体积可以通过测量出水的高度和瓶子的底面直径并计算得到，可是空气部分是一个不规则的立体图形，无法直接求出体积。 环节三： 再让学生思考：能否将空气部分变成一个规则的立体图形呢？引导学生把瓶子倒置，利用水和空气的易变形性，把空气部分变成一个规则的立体图形。在瓶子倒置前后，水的体积不变，空气的体积不变，因此，瓶子的容积等于倒置前水的体积加上倒置后空气的体积，这两部分体积都可以通过测量相关数据求得。 圆锥体积的微积分求法 r h x 设任一平行于底面的截面，圆锥顶点到它的距离是 x ，则根据相似三角形的性质，可求出它的半径是 xr / h 。 它的面积是 π （ xr / h ） 2 = （ π r 2 / h 2 ） x 2 圆锥体积就是 = （ π r 2 / h 2 ）（ h 3 /3-0 3 ） = π r 2 h /3 2 2 2 四、教学中需注意的问题 加强数学知识与实际生活的联系，提高运用所学知识解决实际问题的意识与能力。 引导学生经历知识的探索过程，培养自主解决问题的能力。 3. 充分关注操作与想象相结合，发展学生的空间观念。 第四单元 比例 一、教学内容 比例的意义和基本性质 正比例和反比例 比例的应用 二、与实验教材的主要区别 “比例的基本性质”中增加了让学生用字母来表示比例基本性质的内容，以促进学生思维的一般化。 将标题“成正比例的量”“成反比例的量”改成“正比例”“反比例”，更加突出量与量之间的“关系”，充分体现函数思想。 改编了正比例的素材。 增加一道求比例尺的例题，同时，改编了应用比例尺画平面图的例题，降低了难度。 练习部分增加了一些有利于学生自主探究、有利于培养学生实践能力的综合性习题。 三、具体编排 比例 比例的意义和基本性质 正比例和反比例 比例的意义 例 1 比例的基本性质 例 4 例 5 、例 6 正比例 反比例 例 1 例 2 、例 3 解比例 例 2 比例的应用 比例尺 例 1 、例 2 、例 3 图形的放大与缩小 用比例解决问题 比例式中的对应性 2.4︰1.6 = 60︰40 2.4︰60 = 1.6︰40 40︰1.6 = 60︰2.4 40︰60 = 1.6︰2.4 1.6︰2.4 = 40︰60 1.6︰40 = 2.4︰60 60︰2.4 = 40︰1.6 60︰40 = 2.4︰1.6 解比例方法的多样性 为什么换素材？ 所用的还是原来的数量关系 四、教学中需注意的问题 1 ．应让学生理解变量、常量等概念，初步渗透函数思想。 从数到量，从计算到关系，从算术到代数。 同样是某一数量关系的掌握和运用，角度发生了变化。 C= π d ，所以当直径不变时，圆的周长与圆周率成正比例关系。 《 数学课程标准（ 2011 年版） 》 ：世界是运动变化的，函数是研究运动变化的重要数学模型，与实际的联系十分紧密，它来源于实际又服务于实际，从实际中抽象出函数的有关概念，又运用函数解决实际问题，这是学习函数的主要目标。在建立和运用函数模型的过程中， 变化和对应的思想 是重要的基础， 函数就是从数量的角度反映变化规律和对应关系的数学模型 。 函数思想 认识到这个世界是普遍联系的，各个量之间总是有互相依存的关系，即 “普遍联系” 的观点； 于“变化”中寻求“规律 ( 关系式 )” ，即 “模式化” 思想； 于“规律”中追求 “变化”“对应” 等思想； 根据“规律”判断发展趋势，预测未来，并把握未来，即 “预测” 的思想。于“变化”中把握“规律”，并根据规律做出预测，不仅仅是重要的数学思想，更是人类生存的基本原则。 函数的核心就是 “把握并刻画变化中的不变，其中变化的是‘过程’，不变的是‘规律’ ( 关系 )” 。学生愿意去发现规律，并能将规律表述出来的意识和能力，就是函数思想在教学中的渗透。 2 ．提高学生综合运用知识的能力。 比、比例、解方程、测量（长度、面积）、方位 …… 第五单元 数学广角 —— 鸽巢问题 一、教学内容 抽屉原理 抽屉原理的三种形式 把 m 个物体任意分放进 n 个空抽屉里（ m ＞ n ， n 是非 0 自然数），那么一定有一个抽屉中放进了至少 2 个物体。 把多于个 kn 物体任意分放进 n 个空抽屉里（ k 是正整数），那么一定有一个抽屉中放进了至少（ k +1 ）个物体 。 把无限多个物体任意分放进个空抽屉，那么一定有一个抽屉中放进了无限多个物体。 二、与实验教材的主要区别 增加了扑克牌魔术的主题图。 对例 2 的数据进行了调整。 三、具体编排 4 支铅笔放进 3 个笔筒 7 本书放进 3 个抽屉 在 4 个红球和 4 个蓝球中摸出 2 个同色球（逆向应用） 鸽巢问题 例 1 例 2 例 3 四、教学中需注意的问题 应让学生初步经历“数学证明”的过程。 要有意识地培养学生的“模型思想”。 重视实践活动，在自主探究中理解原理，由具体的情形推广到一般。 要恰当把握教学要求。 第六单元 整理和复习 一、教学内容 数与代数 图形与几何 统计与概率 数学思考 综合与实践 整理与复习的总体目标 整理 —— 完善知识体系 复习 —— 巩固知识技能 沟通 —— 达到融会贯通 提升 —— 做好中小衔接 紧紧围绕课标所提出的十个核心概念 数感 符号意识 空间观念 几何直观 数据分析观念 运算能力 推理能力 模型思想 应用意识 创新意识 体现综合性 数形结合 寻找模式、推理 多样性 代数式、代入求值 奇、偶数的一般式 用数对表示位置 用方向与距离表示位置 路线 数形结合 等腰三角形 化繁为简 探究模式 模式背后的原理 推理 代数式 数形结合 不分主客场 分主客场 北京 高碑店 保定 石家庄 二、与实验教材的主要区别 把“数学思考”独立出来与四部分内容并列复习。 新增两个“综合与实践”活动。 具体内容的编排进行了较大变动。 三、具体编排 统计与概率 整理和复习 综合与实践 有趣的平衡 邮票中的数学问题 图形与几何 图形的认识与测量 图形的运动 图形与位置 数与代数 数的运算 式与方程 比和比例 数学思考 数的认识 绿色出行 北京五日行 （一）基本知识的整理与复习 1 ．以点带面，突出核心概念、核心原理。 2 ．加强知识的横、纵向联系，帮助学生建立网络状的知识结构。 S=a 2 S=ah S=ah S = ah 1 2 S = ( a+b ) h 1 2 S =  r 2 r a ＝ b b ＝ 0 b a h a ＝ b=h 有一组对边平行的四边形面积等于这组对边的平均长度（中位线的长度）乘高。 （ 二 ）基本 技能 的 全面提升 运算能力、读图能力、操作能力、问题解决能力、空间想象能力、数据分析能力、实践能力 （ 三 ） 基本思想 的 体会与掌握 合情推理 演绎推理 等量代换 等式的传递性 ∠ 1+ ∠ 2 =180 º ， ∠ 2+ ∠ 3 =180 º ∠ 1=180 º- ∠ 2 ，∠ 3=180 º- ∠ 2 ∠ 1+ ∠ 2 = ∠ 2+ ∠ 3 ∠ 1= ∠ 3 ∠ 1+ ∠ 4 =180 º ∠ 3+ ∠ 4 =180 º （ 四 ）基本活动经验的不断积累 对知识分门别类进行整理的经验 梳理知识之间联系的经验 综合运用各方面知识解决实际问题的经验 在生活实践中应用数学的经验 …… 四、教学中需注意的问题 加强整理和复习的系统性。 关注概念的理解。 启发、引导学生在理解的基础上自主整理知识。 在系统整理、复习的过程中注意查漏补缺。 加强练习的针对性、有效性。 注意引导学生积累数学 学习 的经验，总结问题 解决 的策略。 感谢聆听 敬请指正