小升初数学模拟试卷（29） 13页

人教新课标小升初数学模拟试卷（29）‎ ‎1．（4分）口算 ‎6.24﹣2.4= +÷= 992+99= 3.16﹣（7.23﹣6.84）=‎ ‎2．（4分）估算 ‎71×39≈ 27.04÷8.92≈ 3.17万+6.9万≈ 291090﹣9986≈‎ ‎3．（3分）笔算 ‎（1）1﹣（﹣）+‎ ‎（2）36×（+）×5 ‎ ‎（3）：=．‎ ‎4．（3分）学校的操场长120米，宽90米，把它画在长30厘米，宽25厘米的长方形纸上，选用（　　）的比例尺比较适当．‎ A.1：400 B.1：500 C.1：1000 D.1：100‎ ‎5．（3分）如图，按一定的流量向放在水槽底部的圆柱体玻璃杯注水，注满玻璃杯后，继续注水，直至注满水槽，水槽中水面上升的高度与注水时间的关系图象大致是（　　）‎ A. B. C. D.‎ ‎6．（3分）1千克黄可以换3千克豆腐．王大妈用黄豆去换豆腐，连同篮子一共称得2千克，换回的豆腐连同这个篮子共重6千克，在这次交易中王大妈（　　）‎ A.赚了 B.亏了 C.不赚不亏 D.赚了还是亏了不能确定 ‎7．（3分）一所学校每个班的平均人数是50.4人，该校班级可能是（　　）个．‎ A.36 B.25 C.24 D.18‎ ‎8．（3分）图中每个小方格表示1平方厘米，左起第（　　）个图形的面积与其他三个不相等．‎ A.A B.B C.C D.D ‎9．（3分）在一个盒子中有10个红球、8个绿球和一些黑球．每次从里面拿出一个球，结果拿出绿球的可能性小于，那么至少有多少个黑球？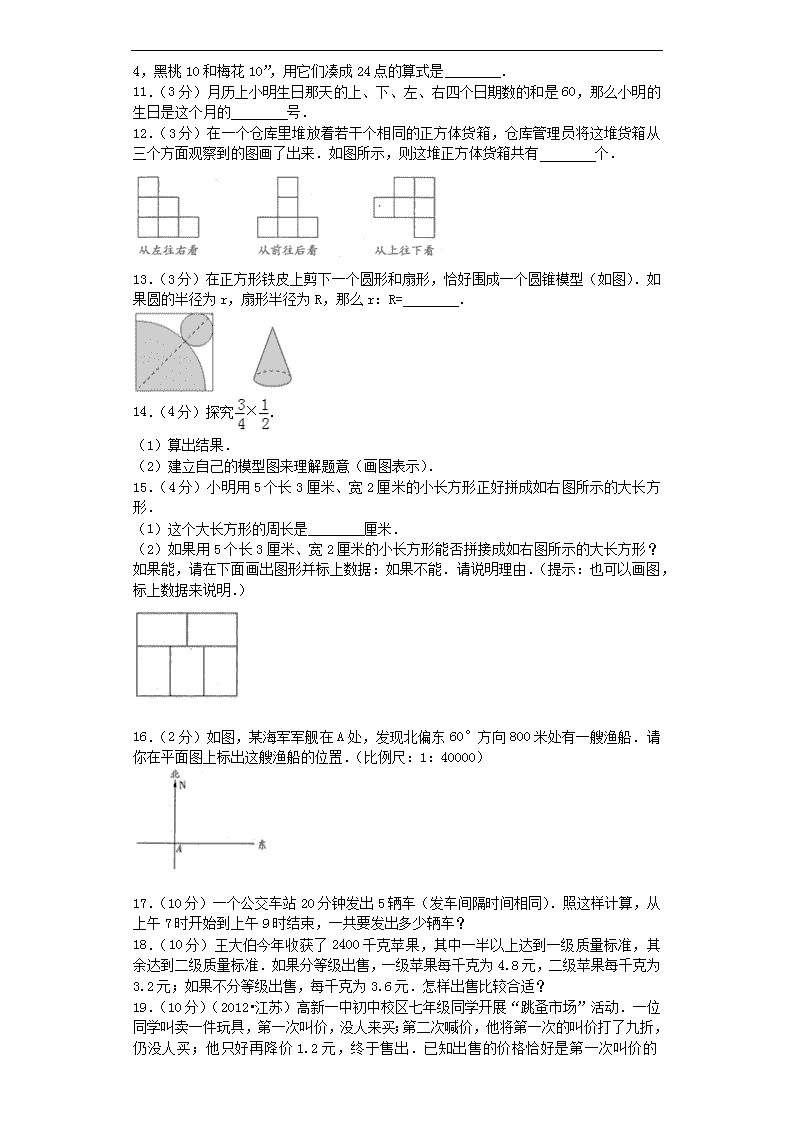‎ ‎10．‎ ‎（3分）算“24”点是我国传统的数学游戏，这里有四张扑克牌：“红桃2，方块4，黑桃10和梅花10”，用它们凑成24点的算式是　 　．‎ ‎11．（3分）月历上小明生日那天的上、下、左、右四个日期数的和是60，那么小明的生日是这个月的　 　号．‎ ‎12．（3分）在一个仓库里堆放着若干个相同的正方体货箱，仓库管理员将这堆货箱从三个方面观察到的图画了出来．如图所示，则这堆正方体货箱共有　 　个．‎ ‎13．（3分）在正方形铁皮上剪下一个圆形和扇形，恰好围成一个圆锥模型（如图）．如果圆的半径为r，扇形半径为R，那么r：R=　 　．‎ ‎14．（4分）探究×．‎ ‎（1）算出结果．‎ ‎（2）建立自己的模型图来理解题意（画图表示）．‎ ‎15．（4分）小明用5个长3厘米、宽2厘米的小长方形正好拼成如右图所示的大长方形．‎ ‎（1）这个大长方形的周长是　 　厘米．‎ ‎（2）如果用5个长3厘米、宽2厘米的小长方形能否拼接成如右图所示的大长方形？如果能，请在下面画出图形并标上数据：如果不能．请说明理由．（提示：也可以画图，标上数据来说明．）‎ ‎16．（2分）如图，某海军军舰在A处，发现北偏东60°方向800米处有一艘渔船．请你在平面图上标出这艘渔船的位置．（比例尺：1：40000）‎ ‎17．（10分）一个公交车站20分钟发出5辆车（发车间隔时间相同）．照这样计算，从上午7时开始到上午9时结束，一共要发出多少辆车？‎ ‎18．（10分）王大伯今年收获了2400千克苹果，其中一半以上达到一级质量标准，其余达到二级质量标准．如果分等级出售，一级苹果每千克为4.8元，二级苹果每千克为3.2元；如果不分等级出售，每千克为3.6元．怎样出售比较合适？‎ ‎19．‎ ‎（10分）（2012•江苏）高新一中初中校区七年级同学开展“跳蚤市场”活动．一位同学叫卖一件玩具，第一次叫价，没人来买；第二次喊价，他将第一次的叫价打了九折，仍没人买；他只好再降价1.2元，终于售出．已知出售的价格恰好是第一次叫价的66%．这位同学第一次给这件玩具叫价多少元？‎ ‎20．（10分）一个圆柱被切成四块（图1），表面积增加48平方厘米，如被切成三块（图2），表面积增加50.24平方厘米，若把它削成一个最大的圆锥体（图3），圆锥体的体积是多少立方厘米？‎ ‎21．（4分）阅读下面的材料，并回答问题．‎ 罗马数字是古罗马使用的数字体系，现在仍在使用．罗马数字共有7个，它们与我们常用的阿拉伯数字的关系为：I代表1，V代表5，X代表10，L代表50，C代表100，D代表500，M代表1000．罗马数字的表示有如下规则：‎ ‎①某个罗马数字重复几次代表的数就是那个罗马数字的几倍，如XX表示20；②在一个较大的罗马数字的右边记上一个较小的罗马数字，表示大数字加小数字，如Ⅶ表示7；③在一个较大的罗马数字的左边记上一个较小的罗马数字，表示大数字减小数字，如Ⅳ表示4．‎ 根据上述材料，罗马数字CD表示　 　；12用罗马数字表示是　 　．‎ ‎22．（5分）“※”表示一种新的运算规则，如8※3=8+9+10=27，3※4=3+4+5+6=18（加数为连续自然数），根据这样的运算规则则完成下面各题．‎ ‎（1）计算：9※6‎ ‎（2）阅读、思考并填空．‎ 在8※3=8+9+10=27中，用27÷3=9，9是8、9、10三个加数的平均数，也是8和10正中间的一个数．‎ 在3※4=3+4+5+6=18中，用18÷4=4.5，4.5是3、4、5、6四个加数的平均数，也是3和6正中间的一个数．‎ 因为x※5=250中，用250÷5=50，可知：‎ 五个加数正中间的一个数是　 　；五个加数是（　 　、　 　、　 　、　 　、　 　）；所以x是　 　．‎ ‎（3）你知道x※22=671中的x是多少吗？简要写出你的想法．‎ 参考答案 ‎1．3.84；1 ；9900；2.77‎ ‎【解析】‎ 试题分析：运用小数的减法及分数的除法及加法的计算法则进行计算，在计算99的平方时要知道是表示两个99相乘，不是99乘以2．‎ 解：6.24﹣2.4=3.84‎ ‎+÷=1‎ ‎992+99=9900‎ ‎3.16﹣（7.23﹣6.84）=2.77‎ 点评：本题考查了小数、分数的四则运算的计算法则，同时考查了数的估算．‎ ‎2．2800；3；10；290000；‎ ‎【解析】‎ 试题分析：根据整数乘法的估算方法，利用“四舍五入法”，把因数看作与它接近的整十数、整百数…；然后进行口算即可．‎ 解：‎ ‎71×39≈70×40=2800‎ ‎27.04÷8.92≈27÷9=3‎ ‎3.17万+6.9万≈3+7=10‎ ‎291090﹣9986≈300000﹣10000=290000．‎ 点评：此题考查的目的是掌握整数乘法的估算方法．‎ ‎3．（1）2；（2）183；（3）x=．‎ ‎【解析】‎ 试题分析：（1）先去括号，再运用加法的交换律简算；‎ ‎（2）运用乘法的分配律进行简算；‎ ‎（3）根据比例的基本性质，两内项之积等于两外项之积，把原式改写成x=×6，然后等式的两边同时除以即可．‎ 解：（1）1﹣（﹣）+‎ ‎=1﹣++‎ ‎=（1+）+（﹣）‎ ‎=2+‎ ‎=2；‎ ‎（2）36×（+）×5 ‎ ‎=36××5+×36×5 ‎ ‎=75+108‎ ‎=183；‎ ‎（3）：=‎ x=×6‎ x=‎ ‎ x=．‎ 点评：此题主要考查分数的四则混合运算，注意运用运算定律进行简便计算，还考查了解比例，根据比的基本性质和等式的性质进行解答即可．‎ ‎4．C ‎【解析】‎ 试题分析：实际距离和比例尺已知，依据“图上距离=实际距离×比例尺”即可求出操场的长和宽的图上距离，再与练习本的实际长度比较即可选出合适的答案．‎ 解：因为120米=12000厘米，90米=000厘米，‎ A、12000×=30厘米，9000厘米×=22.5（厘米），把它画在长30厘米，宽25厘米的长方形纸上，不符合实际情况，故不合适；‎ B、12000×=24（厘米），8000÷=16（厘米），画在练习本上，尺寸过大，不符合实际情况，故不合适；‎ C、12000×=12（厘米），9000×=9（厘米），画在练习本上比较合适；‎ D、12000×=120（厘米），9000×=90（厘米），尺寸过大，不符合实际情况，故不合适；‎ 故选：C．‎ 点评：此题主要考查图上距离、实际距离和比例尺的关系，解答时要注意结合实际情况．‎ ‎5．B ‎【解析】‎ 试题分析：本题中的时间可分为三个段．第一段从注水开始到水注满烧杯结束，在这段时间内水槽的水面高度为零；第二段时间从水槽内有水开始到高度上升到烧杯的高度为止，在这段时间内水槽内水的高度迅速增加；第三段时间从水到烧杯高度开始到水槽内的水注满结束，在这段时间内水槽内的水的高度缓慢增加．所以在图象上表示为第一段时间内高度为零，由于第三段时间内水高上升的速度要比第二段时间内上升的缓慢，在图象上表示为第三部分要比第二部分平缓，所以应选择B答案．‎ 解：如图，‎ 向放在水槽底部的烧杯注水（流量一定）注满烧杯后，继续注水，直至注满水槽，水槽中水面上升高度与注水时间之间的关系大致图象是：‎ ‎；‎ 故选：B 点评：关键是第一段从注水开始到水注满烧杯结束，在这段时间内水槽的水面高度为零，第三段时间内水高上升的速度要比第二段时间内上升的缓慢．‎ ‎6．A ‎【解析】‎ 试题分析：首先根据题意，可得豆腐比黄豆重：6﹣2=4（千克），然后根据1千克黄可以换3千克豆腐，可以求出原来的黄豆的重量，进而判断出在这次交易中王大妈是赚了还是亏了．‎ 解：豆腐比黄豆重：6﹣2=4（千克），‎ 原来的黄豆重量：4÷（3﹣1）×1=2（千克），‎ 因为黄豆连同篮子一共称得2千克，‎ 所以原来的黄豆少于2千克，‎ 所以在这次交易中王大妈赚了．‎ 故选：A．‎ 点评：解答此题的关键是首先求出豆腐比黄豆重4千克，进而求出正常情况下原来的黄豆重量．‎ ‎7．B ‎【解析】‎ 试题分析：根据“总人数=平均每班人数×班级个数”，由于平均每班50.4人，在现实生活中，人数只能是整数，所以班级的个数只能是个位是0或5的数，据此解答．‎ 解：由分析结合给出的四个数可知，‎ 算出的学校平均每班人数为50.4人，他们学校的班级数的个位数字只能是5，所以可能是25个班，‎ 故选：B．‎ 点评：本题根据平均数的含义和生活实际进行解答即可．‎ ‎8．C ‎【解析】‎ 试题分析：根据图分别得出A、B、C、D四个图形的面积，然后进行比较即可．‎ 解：A图形的面积是3平方厘米；‎ B图形的面积是3平方厘米；‎ C图形的面积是2.5平方厘米；‎ D图形的面积是3平方厘米；‎ 所以C图形的面积与其它三个不相等；‎ 故选：C．‎ 点评：求出四个图形的面积，是解答此题的关键．‎ ‎9．7个 ‎【解析】‎ 试题分析：假设摸出绿球的可能性等于，即盒子中球的总个数的是绿球的个数，根据已知一个数的几分之几是多少，求这个数，用除法求出盒子中球的总个数，然后减去盒子中红球和绿球的个数，即盒子中黑球个数；因为拿出绿球的可能性小于，所以用求出的黑球个数加1即可．‎ 解：8÷=24（个），‎ ‎24﹣10﹣8+1，‎ ‎=6+1，‎ ‎=7（个）；‎ 答：至少有7个黑球．‎ 点评：解答此题用到的知识点：先进行假设，进而根据已知一个数的几分之几是多少，求这个数，用除法求出盒子中球的总个数，然后求出当摸出绿球的可能性等于时黑球的个数，然后加1即可．‎ ‎10．10×（2+4÷10）．‎ ‎【解析】‎ 试题分析：根据数的特点，进行试填运算符号，可得：2+4÷10=2.4，2.4=24；据此写出即可．‎ 解：10×（2+4÷10）‎ ‎=10×2.4‎ ‎=24‎ 故答案为：10×（2+4÷10）．‎ 点评：解答此类题的关键是认真审题，根据数的特点，进行试填运算符号，进而得出结论．‎ ‎11．15‎ ‎【解析】‎ 试题分析：左边的数比小明生日日期小1，右边的数比小明的生日日期大1，上边的数比小明的生日日期小7，下边的数比小明的生日日期大7，让这4个数相加等于60列方程求解即可．‎ 解：设小明的生日是x号．‎ ‎（x﹣1）+（x+1）+（x﹣7）+（x+7）=60‎ ‎ 4x=60‎ ‎ x=15‎ 答：小明的生日是这个月的 15号．‎ 故答案为：15．‎ 点评：考查一元一次方程的应用，得到用生日日期表示的上、下、左、右四个日期是解决本题的突破点；用到的知识点为：日历中横行上相邻的2个数相邻1，竖列上相邻2个相差7．‎ ‎12．9‎ ‎【解析】‎ 试题分析：易得这个几何体共有3层，由俯视图可得第一层正方体的个数，由正视图和左视图可得第二层，第三层正方体的个数，相加即可．‎ 解：由俯视图可得最底层有6个，由正视图和左视图可得第二层有2个，第三层有1个箱，‎ 共有：6+2+1=9（个）；‎ 答：这堆正方体货箱共有9个．‎ 故答案为：9．‎ 点评：考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，主视图疯狂盖，左视图拆违章”就更容易得到答案．‎ ‎13．1：2‎ ‎【解析】‎ 试题分析：根据围成圆锥后圆锥的侧面展开扇形的弧长等于圆锥的底面周长，列出关系式即可得到两个半径之间的关系．‎ 解：因为扇形的弧长等于圆锥底面周长，‎ 所以×2πR=2πr R=r r：R=1：2；‎ 故答案为：1：2．‎ 点评：解答此题的关键是明白：圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长．‎ ‎14．（1）；‎ ‎（2）‎ ‎=，把平均分成2份，×=‎ ‎【解析】‎ 试题分析：（1）运用分数乘法的计算法则进行计算即可．‎ ‎（2）=所以把一个长方形的平均分成8份，取其中的6份，就是=，把平均分成2份，其中一份是．‎ 解：（1）=‎ ‎（2）‎ ‎=，把平均分成2份，‎ ‎×=‎ 点评：本题运用分数乘法的计算法则进行计算即可，注意把化成分母是8的分数，然后再表示出的一半．‎ ‎15．（1）22厘米．‎ ‎（2）‎ ‎【解析】‎ 试题分析：（1）由图知，大长方形的长是3+3=6厘米，宽是3+2=5厘米，根据长方形的周长=（长+宽）×2解答即可；‎ ‎（2）由题1可知，能用5个长3厘米、宽2厘米的小长方形能否拼接成如右图所示的大长方形，据此画图即可．‎ 解：（1）3+3=6（厘米），‎ ‎3+2=5（厘米），‎ ‎（6+5）×2=22（厘米）；‎ 答：这个大长方形的周长是22厘米．‎ ‎（2）由题1可知，能用5个长3厘米、宽2厘米的小长方形能拼接成如右图所示的大长方形，‎ 如下图：‎ 故答案为：22．‎ 点评：解答此题的关键是明白：大长方形的长、宽各包括几部分．‎ ‎16．‎ ‎【解析】‎ 试题分析：800米=80000厘米．根据实际距离和比例尺，算出图上距离为：80000×=2（厘米）．然后根据方向和距离画出渔船的位置即可．‎ 解：渔船的位置如下：‎ 点评：本题的关键是根据图上距离=实际距离÷比例尺，求出图上距离，再根据方向画图．‎ ‎17．25辆车 ‎【解析】‎ 试题分析：根据“20分钟发出5辆车”可知：发5辆车经过了4个间隔时间，每个时间间隔为：20÷4=5分钟；从上午7时到上午9时经过了2×60=120分钟；一共要发出的辆数是：120÷5+1=25辆，即可求出．‎ 解：20÷（5﹣1）‎ ‎=20÷4‎ ‎=5（分钟）‎ ‎9﹣7=2（小时）‎ ‎2×60÷5+1‎ ‎=120÷5+1‎ ‎=25（辆）‎ 答：一共要发出25辆车．‎ 点评：本题的难点是理解发5辆车经过了4个间隔时间，间隔数=发车辆数﹣1．‎ ‎18．分级出售收入多些．‎ ‎【解析】‎ 试题分析：由题意可知，共有2400千克苹果，其中一半以上达到一级质量标准，即达到一级的有2400÷2=1200千克，2400﹣1200=1200千克是二级，分等级出售，一级苹果每千克为4.8元，根据乘法的意义，一级可卖1200×4.8元，同理二级可卖1200×3.2元，则共可卖1000×2.4+1000×1.6元；‎ 如果不分等级出售，每千克为3.6元，则共可卖2400×3.6元．计算后即可知怎样出售获得的收入多一些，比较即可解答．‎ 解：分级出售：‎ ‎（2400÷2）×4.8+（2400﹣2400÷2）×3.2‎ ‎=1200×4.8+1200×3.2‎ ‎=1200（4.8+3.2）‎ ‎=1200×8‎ ‎=9600（元）‎ 不分级出售 ‎2400×3.6=8640（元）‎ ‎9600＞8640．‎ 答：分级出售收入多些．‎ 点评：完成本题也可根据其中一半以上达到一级质量标准，其余达到二级质量标准，得出分级出售的平均价格是（4.8+3.2）÷2=4元/千克，从而得出结论．‎ ‎19．5元 ‎【解析】‎ 试题分析：把第一次叫价的钱数看成单位“1”，那么它的（90%﹣66%）对应的数量就是1.2元，由此用除法求出第一次叫价的价格．‎ 解：1.2÷（90%﹣66%），‎ ‎=1.2÷24%，‎ ‎=5（元）；‎ 答：这位同学第一次给这件玩具叫价5元．‎ 点评：本题的关键是找出单位“1”，并找出单位“1”的百分之几对应的数量，用除法就可以求出单位“1”的量．‎ ‎20．12.56立方厘米．‎ ‎【解析】‎ 试题分析：根据圆柱的切割特点可知，如图二切割成3块，则表面积是增加了4个圆柱的底面的面积，据此求出一个底面的面积是50.24÷4=12.56平方厘米，根据圆的面积公式可得：r2=12.56÷3.14=4，因为22=4，所以这个圆的半径是2厘米，再根据图一的切割方法，沿底面直径切割后，表面积是增加了8个以底面半径和高为边长的长方形，据此可以求出这个长方形的面积是：48÷8=6平方厘米，因为半径是2厘米，所以利用长方形的面积公式可得，圆柱的高是：6÷2=3厘米，据此求出了圆柱的底面半径和高，再利用圆柱的体积公式即可求出这个圆柱的体积，如图三，把这个圆柱先削成一个最大的圆锥，则圆锥的体积是圆柱体积的．‎ 解：50.24÷4=12.56（平方厘米）；‎ ‎12.56÷3.14=4，因为22=4；‎ 所以这个圆柱的底面半径是2厘米；‎ ‎48÷8÷2‎ ‎=6÷2‎ ‎=3（厘米）；‎ ‎3.14×22×3×‎ ‎=3.14×4‎ ‎=12.56（立方厘米）‎ 答：圆柱的体积是12.56立方厘米．‎ 点评：抓住圆柱的两种切割特点，根据增加的表面积分别求出这个圆柱的底面半径和高，是解决本题的关键．‎ ‎21．400，XII．‎ ‎【解析】‎ 试题分析：根据“累积符号”和“前减后加”的原则来计数，如：小数在大数前就减，在大数后就加．‎ 解：由题意得 CD=500﹣100=400，‎ ‎12=10+1+1=XII．‎ 故答案为：400，XII．‎ 点评：本题主要考查了实数的运算，是一道探索题，解答此题的关键是要弄清其计数方法是用“累积符号”和“前减后加”的原则，再计算．‎ ‎22．（1）69；（2）50；48，49，50，51，52；48；（3）x=20‎ ‎【解析】‎ 试题分析：（1）根据8※3=8+9+10=27，3※4=3+4+5+6=18可知：从左边的数字开始连续自然数相加即可，加数的个数就是右边的数字；‎ ‎（2）根据8※3=8+9+10=27中，用27÷3=9，9是8、9、10三个加数的平均数，也是8和10正中间的一个数；‎ 在3※4=3+4+5+6=18中，用18÷4=4.5，4.5是3、4、5、6四个加数的平均数，也是3和6正中间的一个数；‎ 所以x※5=250中是由5个连续自然数相加，用250÷5=50，可知50是这五个自然数最中间的一个，即可求得这五个数，而这五个数最小的是未知数的值；‎ ‎（3）根据第二问可知：671÷22的值是22个数中中间两个数的平均数，进而求得这22个数，最小的数就是x的值．‎ 解：（1）9※6‎ ‎=9+10+11+12+13+14‎ ‎=（9+14）×3‎ ‎=23×3‎ ‎=69‎ ‎（2）根据题意可知：‎ 因为x※5=250中，用250÷5=50，可知：‎ 五个加数正中间的一个数是50；五个加数是48、49、50、51、52；所以x是48．‎ ‎（3）671÷22=30.5‎ ‎30.5是22个数中最中间的一个，所以30.5左边11个数，右边11个数，分别为：‎ ‎20，21，22，23，24，25，26，27，28，29，30，31，32，33，34，35，36，37，38，39，40，41‎ 最左边的数字就是未知数的取值，所以x=20‎ 答：x=20‎ 故答案为：50；48，49，50，51，52；48‎ 点评：解答本题的关键是：认真分析新规律，按照规律计算即可．‎