六年级下册数学教案 成正比例的量 冀教版 (1) 5页

‎《成正比例的量》教学设计 教学目标:‎ ‎1、结合丰富的实例，引导学生认识正比例，理解正比例的意义，掌握正比例的字母表达式 ‎2、能根据正比例的意义，会正确判断两个量是不是成正比例关系的两个量，能找出生活中成正比例量的实例，并进行交流。‎ ‎3、在具体的生活情境中，经历操作、观察、对比、归纳的学习过程，学会在生活中体验知识，运用知识，感受数学和生活的密切联系。培养学生的抽象概括和分析判断能力。‎ ‎4、渗透函数思想，初步建立事物是相互联系的辩证观念。‎ 教学重点: 理解正比例的意义，并能判断两种相关联的量是否成正比例。‎ 教学难点: 通过观察思考发现两种相关联的量的变化规律从而概括出正比例的意义。‎ 教学过程：‎ 一、出示情境 感知量的关系 ‎1、看图猜成语：水涨船高、风吹草动 现实中，一个事件的发生引起另一个事件的发生，我们就可以说这两个事件是相关联的。‎ 在数学中，也存在着一个量的变化引起另一个量的变化这样的现象。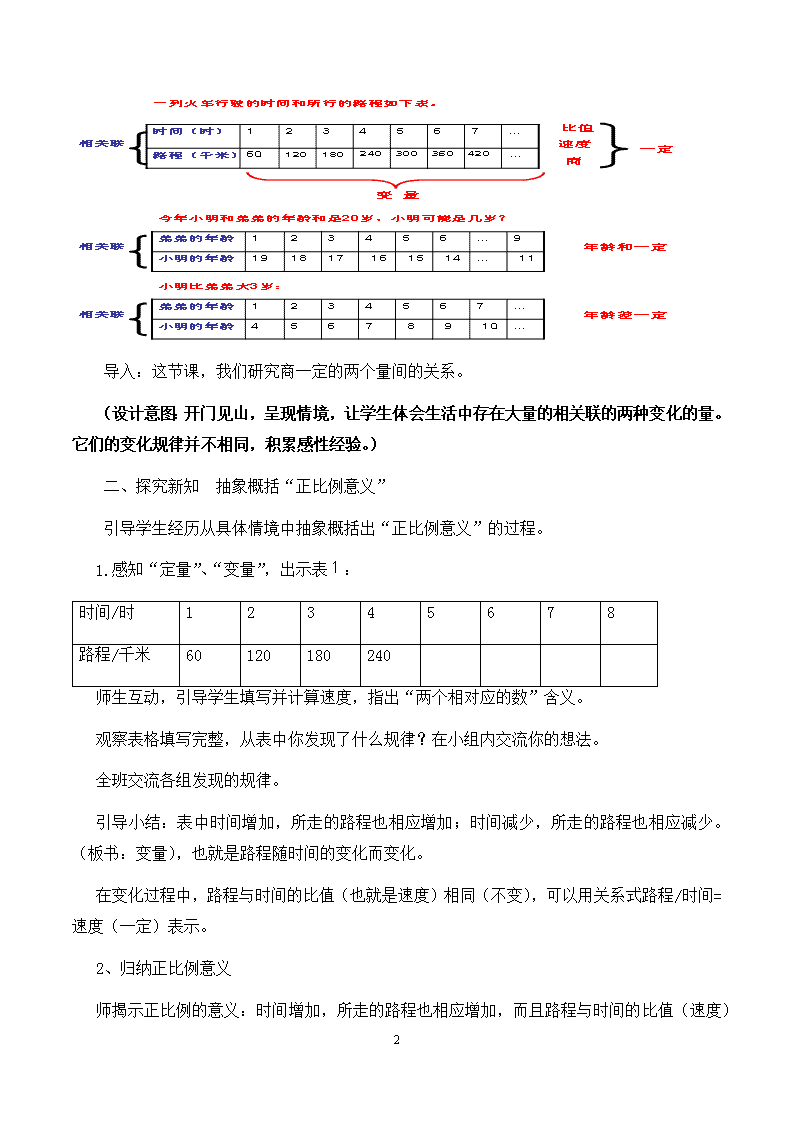例如：‎ 多媒体逐表演示，引导观察分析感知“相关联的两个量”；“和一定”“差一定”“商一定”的两个量。‎ 5‎ 导入：这节课，我们研究商一定的两个量间的关系。‎ ‎（设计意图：开门见山，呈现情境，让学生体会生活中存在大量的相关联的两种变化的量。它们的变化规律并不相同，积累感性经验。）‎ 二、探究新知 抽象概括“正比例意义”‎ 引导学生经历从具体情境中抽象概括出“正比例意义”的过程。‎ ‎1.感知“定量”、“变量”，出示表１： ‎ 时间/时 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 路程/千米 ‎60‎ ‎120‎ ‎180‎ ‎240‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 师生互动，引导学生填写并计算速度，指出“两个相对应的数”含义。‎ 观察表格填写完整，从表中你发现了什么规律？在小组内交流你的想法。‎ 全班交流各组发现的规律。‎ 引导小结：表中时间增加，所走的路程也相应增加；时间减少，所走的路程也相应减少。（板书：变量），也就是路程随时间的变化而变化。‎ 在变化过程中，路程与时间的比值（也就是速度）相同（不变），可以用关系式路程/时间=速度（一定）表示。‎ ‎2、归纳正比例意义 5‎ 师揭示正比例的意义：时间增加，所走的路程也相应增加，而且路程与时间的比值（速度）相同。那么，我们说路程和时间成正比例。‎ 谁能用自己的话归纳什么是成正比例？‎ 学生表述，师适时引导对照板书。‎ 讲评归纳：两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的比值（也就是商）一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。‎ ‎3、正比例字母表达式 观察表格，质疑：表中两个相对应的数能填的完吗？我们可以怎样表示？‎ ‎（一定）‎ 这里的Y表示什么？X表示什么？K表示什么？‎ ‎3、总结成“正比例关系”的条件 出示表2中，所付的钱数与圆珠笔支数成正比例吗？为什么？‎ A、相关联 B、变量：一种量变化，另一种量也随着变化。‎ C、定量：两种量中相对应的两个数的比值相同。‎ ‎（设计意图：借助一系列的情境，为学生理解“正比例的意义”提供了丰富的直观背景和具体案例。采用“引”、“扶”的方法学习表1，让学生再次体会正比例意义的特征。通过“放”让学生自学表2,体会正比例意义的本质特征。然后通过观察、比较、讨论，水到渠成引出正比例的意义，使抽象的数学概念，通过具体式子60/1=120/2=… …480/8=60(相同)，变得让学生看得见，摸得着了）。‎ 三、巩固应用，加深对正比例意义的理解 ‎1、下表是矿泉水的数量和总价的关系，回答下列问题：‎ 5‎ 数量/瓶 ‎5‎ ‎10‎ ‎15‎ ‎20‎ ‎25‎ 总价/元 ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎（１）5瓶的售价是 元，12瓶的售价是 元， 瓶的售价是36元。‎ ‎（２）王明买矿泉水的瓶数量是李红的3倍，王明所花的钱数是李红的 倍。所以 与 成正比例。‎ ‎2、判断下面各题中的两个量是否成正比例，并说说理由。‎ ‎（１）每袋大米的质量一定，大米的总质量和袋数。‎ ‎（２）一个人的身高和年龄。‎ ‎（３）宽不变，长方形的周长和长。‎ ‎3、‎ ‎（设计意图：通过有梯度、针对性的对比练习，一是想激发学生的练习的兴趣，通过辨别，克服学生的思维定势：认为只要一个量随着另一个量的增加而增加，减少而减少，两个量就成正比例；二是形成“正比例意义”的正确表象；三是感受正比例在生活中的广泛应用，体会数学与生活的密切联系；四是学生感知必要条件的含义。）‎ 四、全课总结并揭示课题：通过这节课的学习，你都知道了什么？（随机板书课题：正比例的意义）怎么判断两种相关联的量是否成正比例？‎ 5‎ 板书：  正比例的意义 ‎ 路程：时间=速度（一定） 路程和时间成正比例 总价：数量=单价（一定） 总价和数量成正比例 两个量相关联 判断方法 变量：（一种量变化，另一种量也随着变化）‎ ‎ 定量：（ 相对应的两个数的比值一定） ‎ 这两种相关联的量就成正比例 5‎