2011中考数学真题解析82中位线含答案 29页

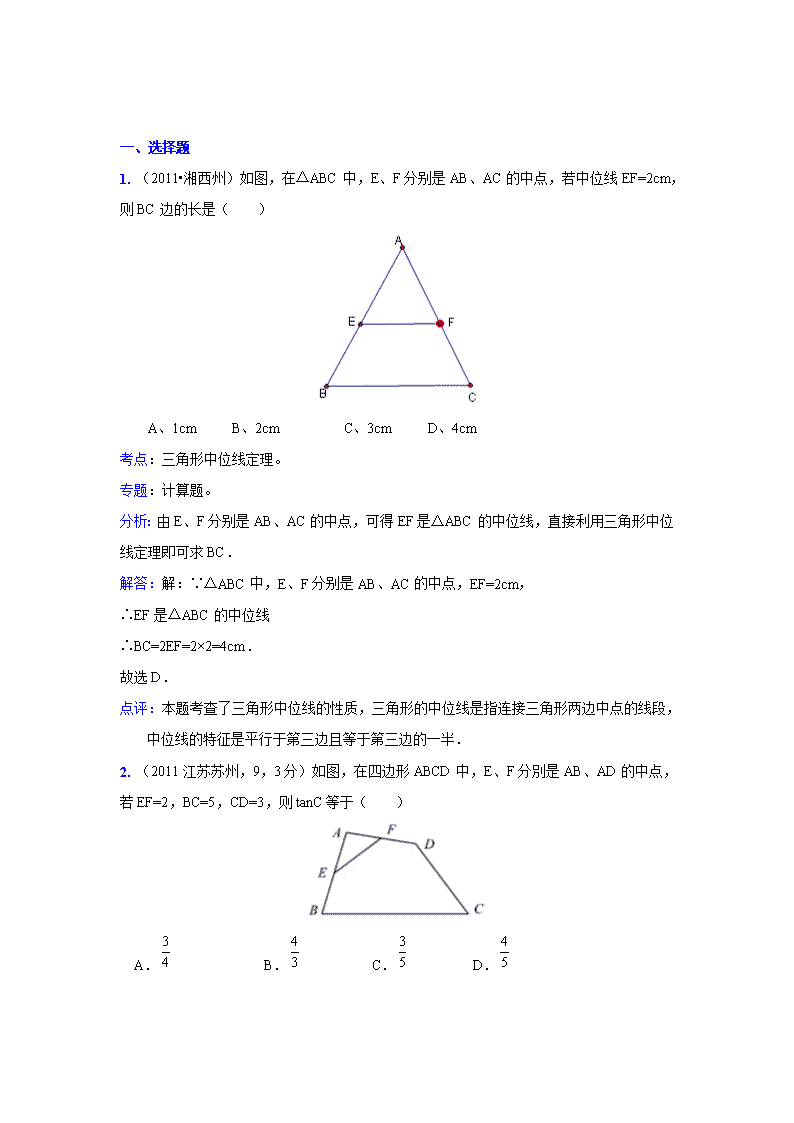
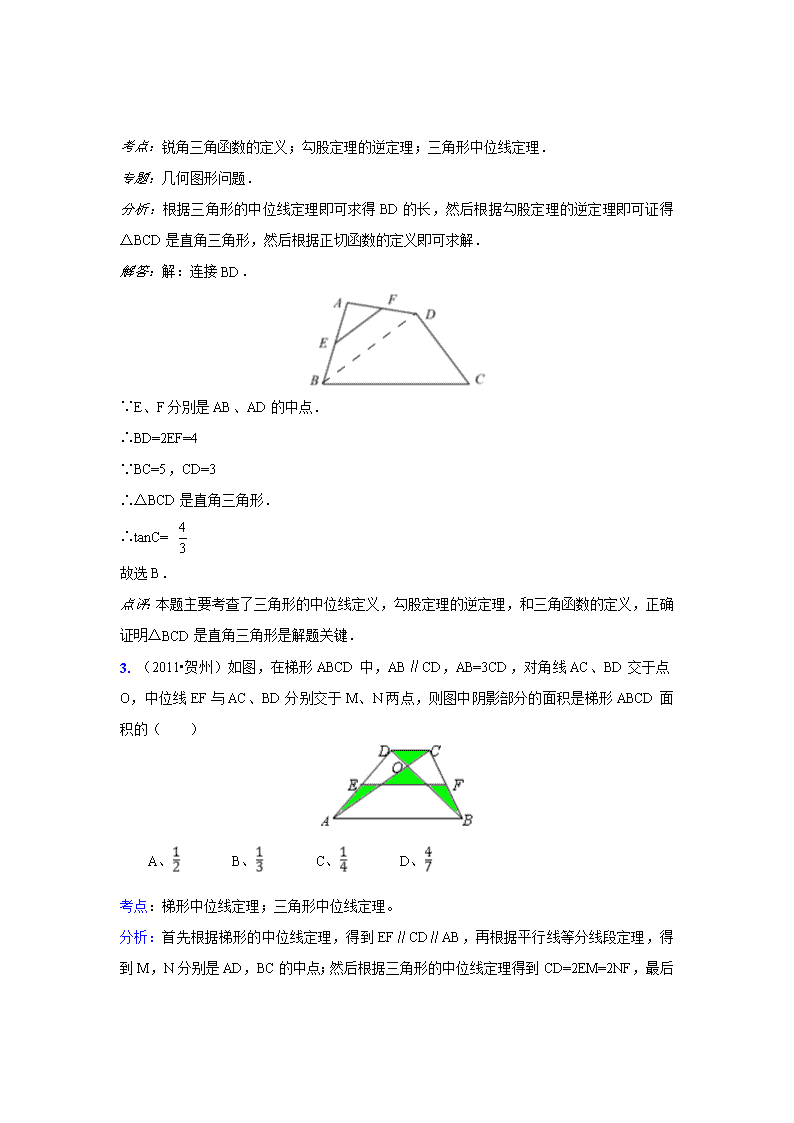
一、选择题 ‎1. （2011•湘西州）如图，在△ABC中，E、F分别是AB、AC的中点，若中位线EF=2cm，则BC边的长是（　　）‎ ‎ A、1cm B、2cm C、3cm D、4cm 考点：三角形中位线定理。‎ 专题：计算题。‎ 分析：由E、F分别是AB、AC的中点，可得EF是△ABC的中位线，直接利用三角形中位线定理即可求BC．‎ 解答：解：∵△ABC中，E、F分别是AB、AC的中点，EF=2cm，‎ ‎∴EF是△ABC的中位线 ‎∴BC=2EF=2×2=4cm．‎ 故选D．‎ 点评：本题考查了三角形中位线的性质，三角形的中位线是指连接三角形两边中点的线段，中位线的特征是平行于第三边且等于第三边的一半．‎ ‎2. （2011江苏苏州，9，3分）如图，在四边形ABCD中，E、F分別是AB、AD的中点，若EF=2，BC=5，CD=3，则tanC等于（　　）‎ ‎ A． B． C． D．‎ 考点：锐角三角函数的定义；勾股定理的逆定理；三角形中位线定理．‎ 专题：几何图形问题．‎ 分析：根据三角形的中位线定理即可求得BD的长，然后根据勾股定理的逆定理即可证得△BCD是直角三角形，然后根据正切函数的定义即可求解．‎ 解答：解：连接BD．‎ ‎∵E、F分別是AB、AD的中点． ∴BD=2EF=4 ∵BC=5，CD=3 ∴△BCD是直角三角形． ∴tanC= 故选B．‎ 点评：本题主要考查了三角形的中位线定义，勾股定理的逆定理，和三角函数的定义，正确证明△BCD是直角三角形是解题关键．‎ ‎3. （2011•贺州）如图，在梯形ABCD中，AB∥CD，AB=3CD，对角线AC、BD交于点O，中位线EF与AC、BD分别交于M、N两点，则图中阴影部分的面积是梯形ABCD面积的（　　）‎ ‎ A、 B、 C、 D、 考点：梯形中位线定理；三角形中位线定理。‎ 分析：首先根据梯形的中位线定理，得到EF∥CD∥AB，再根据平行线等分线段定理，得到M，N分别是AD，BC的中点；然后根据三角形的中位线定理得到CD=2EM=2NF ‎，最后根据梯形面积求法以及三角形面积公式求出，即可求得阴影部分的面积与梯形ABCD面积的面积比．‎ 解答：解：过点D作DQ⊥AB，交EF于一点W，‎ ‎∵EF是梯形的中位线，‎ ‎∴EF∥CD∥AB，DW=WQ，‎ ‎∴AM=CM，BN=DN．‎ ‎∴EM=CD，NF=CD．‎ ‎∴EM=NF，‎ ‎∵AB=3CD，设CD=x，∴AB=3x，EF=2x，‎ ‎∴MN=EF﹣（EM+FN）=x，‎ ‎∴S△AME+S△BFN=×EM×WQ+×FN×WQ=（EM+FN）QW=x•QW，‎ S梯形ABFE=（EF+AB）×WQ=QW，‎ S△DOC+S△OMN=CD×DW=xQW，‎ S梯形FECD=（EF+CD）×DW=xQW，‎ ‎∴梯形ABCD面积=xQW+xQW=4xQW，‎ 图中阴影部分的面积=x•QW+xQW=xQW，‎ ‎∴图中阴影部分的面积是梯形ABCD面积的：=．‎ 故选：C．‎ 点评：此题考查了三角形中位线定理、平行线等分线段定理和梯形的中位线定理和梯形面积与三角形面积求法，解答时要将三个定理联合使用，以及得出各部分对应关系是解决问题的关键．‎ ‎4. （2011•泰州，8，3分）如图，直角三角形纸片ABC的∠C为90°，将三角形纸片沿着图示的中位线DE剪开，然后把剪开的两部分重新拼接成不重叠的图形，下列选项中不能拼出的图形是（　　）‎ ‎ A、平行四边形 B、矩形 C、等腰梯形 D、直角梯形 考点：三角形中位线定理。‎ 专题：作图题。‎ 分析：将剪开的△ADE绕E点顺时针旋转180°，使EA与EB重合，得到矩形，也就是平行四边形，将剪开的△ADE绕D点逆时针旋转180°，使DA与DC重合，得到等腰梯形，故不能得到直角梯形．‎ 解答：解：将剪开的△ADE绕E点顺时针旋转180°，使EA与EB重合，得到矩形，也就是平行四边形，故A、B正确；‎ 将剪开的△ADE绕D点逆时针旋转180°，使DA与DC重合，得到等腰梯形，故C正确；‎ ‎∴不能得到直角梯形，故D错误．‎ 故选D．‎ 点评：本题考查了三角形的中位线定理，旋转的性质．关键是运用中位线的性质，旋转的方法得出基本图形．‎ ‎5.（2011山东滨州，12，3分）如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,‎ 现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )‎ A.1 ( B.2 C.3 D.4‎ ‎【考点】三角形中位线定理．‎ ‎【专题】作图题．‎ ‎【分析】将该三角形剪成两部分，拼图使得△ADE和直角梯形BCDE不同的边重合，即可解题．‎ ‎【解答】解：①使得CE与AE重合，即可构成邻边不等的矩形，如图：‎ ‎∵∠C=60°， ∴AB= BC， ∴BD≠BC． ②使得BD与AD重合，即可构成等腰梯形，如图：‎ ‎③使得BD与DE重合，即可构成有一个角为锐角的菱形，如图：‎ 故计划可拼出①②③． 故选C．‎ ‎【点评】本题考查了三角形中位线定理的运用，考查了三角形中位线定理的性质，本题中求证BD≠BC是解题的关键．‎ ‎6. （2011•莱芜）如图，E、F、G、H分别是BD、BC、AC、AD的中点，且AB=CD．下列结论：①EG⊥FH，②四边形EFGH是矩形，③HF平分∠EHG，④EG=（BC﹣AD），⑤四边形EFGH是菱形．其中正确的个数是（　　）‎ ‎ A、1 B、2 C、3 D、4‎ 考点：三角形中位线定理；菱形的判定与性质。‎ 专题：推理填空题。‎ 分析：根据三角形的中位线平行于第三边并且等于第三边的一半与AB=CD可得四边形EFGH是菱形，然后根据菱形的对角线互相垂直平分，并且平分每一组对角的性质对各小题进行判断．‎ 解答：解：∵E、F、G、H分别是BD、BC、AC、AD的中点，‎ ‎∴EF=CD，FG=AB，GH=CD，HE=AB，‎ ‎∵AB=CD，‎ ‎∴EF=FG=GH=HE，‎ ‎∴四边形EFH是菱形，‎ ‎∴①EG⊥FH，正确；‎ ‎②四边形EFGH是矩形，错误；‎ ‎③HF平分∠EHG，正确；‎ ‎④EG=（BC﹣AD），只有AD∥BC是才可以成立，而本题AD与BC 很显然不平行，故本小题错误；‎ ‎⑤四边形EFGH是菱形，正确．‎ 综上所述，①③⑤共3个正确．‎ 故选C．‎ 点评：本题考查了三角形中位线定理与菱形的判定与菱形的性质，根据三角形的中位线定理与AB=CD判定四边形EFGH是菱形是解答本题的关键．‎ ‎7. （2011年山东省威海市，6，3分）在△ABC中，AB＞AC，点D、E分别是边AB、AC的中点，点F在BC边上，连接DE，DF，EF，则添加下列哪一个条件后，仍无法判定△BFD与△EDF全等（　　）‎ A、EF∥AB B、BF=CF C、∠A=∠DFE D、∠B=∠DEF 考点：全等三角形的判定；平行线的判定与性质；三角形中位线定理．‎ 专题：证明题．‎ 分析：根据平行线的性质得到∠BDF=∠EFD，根据D E分别是AB AC的中点，推出DE∥BC，DE= BC，得到∠EDF=∠BFD，根据全等三角形的判定即可判断A；由DE= BC=BF，∠EDF=∠BFD，DF=DF即可得到△BFD≌△EDF；由∠A=∠DFE证不出△BFD≌△EDF；由∠B=∠DEF，∠EDF=∠BFD，DF=DF，得到△BFD≌△EDF．‎ 解答：解：A、∵EF∥AB， ∴∠BDF=∠EFD， ∵D E分别是AB AC的中点， ∴DE∥BC，DE= BC， ∴∠EDF=∠BFD， ∵DF=DF， ∴△BFD≌△EDF，故本选项错误；‎ ‎ B、∵DE= BC=BF，∠EDF=∠BFD，DF=DF，∴△BFD≌△EDF，故本选项错误； C、由∠A=∠DFE证不出△BFD≌△EDF，故本选项正确； D、∵∠B=∠DEF，∠EDF=∠BFD，DF=DF，∴△BFD≌△EDF，故本选项错误． 故选C．‎ 点评：本题主要考查对全等三角形的判定，平行线的性质，三角形的中位线等知识点的理解和掌握，能求出证全等的3个条件是证此题的关键．‎ ‎8. （2011山东省潍坊， 3，3分）如图，△ABC中．BC=2．DE是它的中位线．下面三个结论：（1）DE=1；(2)△ADE∽△ABC；(3)△ADE的面积与△ABC的面积之比为l：4．其中正确的有( )．‎ A．0个 B．1个 C．2个 D．3个 ‎【考点】相似三角形的判定与性质；三角形中位线定理．‎ ‎【专题】几何综合题．‎ ‎【分析】本题需先根据相似三角形的判定和性质以及三角形的中位线的性质逐个分析，即可得出正确答案．‎ ‎【解答】解：（1）∵△ABC中，BC=2，DE是它的中位线， ∴DE= = =1 故本选项正确； （2）∵△ABC中，DE是它的中位线 ∴DE∥BC ‎ ‎∴△ADE∽△ABC 故本选项正确； （3）∵△ADE∽△ABC，相似比为1：2 ∴△ADE的面积与△ABC的面积之比为1：4． 故本选项正确 故选D．‎ ‎【点评】本题主要考查了相似三角形的判定和性质，在解题时要注意与三角形的中位线的性质相结合是本题的关键．‎ ‎9. （2011山东烟台，6，4分）如图，梯形ABCD中，AB∥CD，点E、F、G分别是BD、AC、DC的中点. 已知两底差是6，两腰和是12，则△EFG的周长是（ ）‎ A.8 B.9 C.10 D.12‎ A B C D E F G ‎（第6题图）‎ 考点：三角形中位线定理；全等三角形的判定与性质.‎ 分析：根据三角形中位线定理易得所求的三角形的各边长为原三角形各边长的一半，那么所求的三角形的周长就等于原三角形周长的一半．‎ 解答：解：∵点E、F、G分别是BD、AC、DC的中点．‎ ‎∴EG+GF=（AD+BC），EF=（DC﹣AB）‎ ‎∵两腰和是12，两底差是6，∴EG+GF=6，FE=3，∴△EFG的周长是6+3=9．故选B．‎ 点评：此题考查的是三角形中位线的性质，即三角形的中位线平行于第三边且等于第三边的一半．‎ ‎10.（2011•山西11，2分）如图，△ABC中，AB=AC，点D、E分别是边AB、AC的中点，点G、F在BC边上，四边形DEFG是正方形．若DE=2cm，则AC的长为（　　）‎ ‎ A、cm B、4cm C、cm D、cm 考点：三角形中位线定理；等腰三角形的性质；勾股定理；正方形的性质。‎ 专题：计算题。‎ 分析：根据三角形的中位线定理可得出BC=4，由AB=AC，可证明BG=CF=1，由勾股定理求出CE，即可得出AC的长．‎ 解答：解：∵点D、E分别是边AB、AC的中点，‎ ‎∴DE=BC，‎ ‎∵DE=2cm，‎ ‎∴BC=4cm，‎ ‎∵AB=AC，四边形DEFG是正方形．‎ ‎∴△BDG≌△CEF，‎ ‎∴BG=CF=1，‎ ‎∴EC=，‎ ‎∴AC=cm．‎ 故选D．‎ 点评：本题考查了相似三角形的判定、勾股定理、等腰三角形的性质以及正方形的性质，是基础题，比较简单．‎ ‎11.（2011四川攀枝花，5，3分）如图，在直角三角形ABC中，∠C=90°，AB=10，AC=8，点E、F分别为AC和AB的中点，则EF=（　　）‎ ‎ A、3 B、4 C、5 D、6‎ 考点：三角形中位线定理；勾股定理。‎ 专题：计算题。‎ 分析：根据三角形的中位线定理的数量关系“三角形的中位线等于第三边的一半”，进行计算．‎ 解答：解：∵直角三角形ABC中，∠C=90°，AB=10，AC=8，∴BC==6，∵点E、F分别为AB、AC的中点，∴EF是△ABC的中位线，EF=BC=×6=3．故选A．‎ 点评：此题考查了三角形的中位线定理，熟练掌握定理内容是解题的关键．‎ ‎12. （2011.四川雅安，9,3分）如图，D、E、F分别为△ABC三边的中点，则下列说法中不正确的为（　　）‎ ‎ A.△ADE∽△ABC B.S△ABF=S△AFC C. D.DF=EF 考点：三角形中位线定理；三角形的面积；相似三角形的判定与性质。‎ 专题：证明题。‎ 分析：根据三角形的中位线定理，可得出DE∥BC，DE=BC，再根据三角形的面积公式，△ADE与△AFC等底同高，从而得出答案．‎ 解答：解：∵D、E、F分别为△ABC三边的中点，‎ ‎∴DE∥BC，DE=BC，‎ ‎∴△ADE∽△ABC，‎ S△ADE=S△ABC，‎ ‎∴S△ABF=S△AFC，‎ 故选D．‎ 点评：本题考查了相似三角形的判定和性质、三角形的中位线定理以及三角形的面积，是基础知识要熟练掌握．‎ ‎13. (2011四川雅安9，3分)如图，D．E．F分别为△ABC三边的中点，则下列说法中不正确的为（ ）‎ A △ADE∽△ABC B C D DF=EF 考点：三角形中位线定理；三角形的面积；相似三角形的判定与性质。‎ 专题：证明题。‎ 分析：根据三角形的中位线定理，可得出DE∥BC，DE=BC，再根据三角形的面积公式，△ADE与△AFC等底同高，从而得出答案．‎ 解答：∵D、E、F分别为△ABC三边的中点，‎ ‎∴DE∥BC，DE=BC，‎ ‎∴△ADE∽△ABC，‎ S△ADE=S△ABC，‎ ‎∴S△ABF=S△AFC，‎ 故选D．‎ 点评：本题考查了相似三角形的判定和性质、三角形的中位线定理以及三角形的面积，是基础知识要熟练掌握．‎ ‎14. （2011•黔南，5，4分）如图，△ABC中，AB=AC=6，BC=8，AE平分∠BAC交BC于点E，点D为AB的中点，连接DE，则△BDE的周长是（　　）‎ ‎ A、7+ B、10 C、4+2 D、12‎ 考点：三角形中位线定理。‎ 分析：根据等腰三角形三线合一的性质，先求出BE，再利用中位线定理求出DE即可．‎ 解答：解：∵在△ABC中，AB=AC=6，AE平分∠BAC，‎ ‎∴BE=CE=BC=4，‎ 又∵D是AB中点，‎ ‎∴BD=AB=3，‎ ‎∴DE是△ABC的中位线，‎ ‎∴DE=AC=3，‎ ‎∴△BDE的周长为BD+DE+BE=3+3+4=10．‎ 故选B．‎ 点评：本题主要考查了三角形的中位线定理及勾股定理的运用，是中学阶段的常规题．‎ ‎15. （2011•宜昌，12，3分）如图，在梯形ABCD中，AB∥CD，AD=BC，点E、F、G、H分别是AB，BC，CD，DA的中点，则下列结论一定正确的是（　　）‎ ‎ A、∠HGF=∠GHE B、∠GHE=∠HEF ‎ C、∠HEF=∠EFG D、∠HGF=∠HEF 考点：等腰梯形的性质；三角形中位线定理；菱形的判定与性质。‎ 专题：计算题。‎ 分析：利用三角形中位线定理证明四边形HEFG是平行四边形，进而可以得到结论．‎ 解答：解：连接BD，‎ ‎∵E、F、G、H分别是AB，BC，CD，DA的中点，‎ ‎∴HE∥GE=BD，HE=GE=BD ‎∴四边形HEFG是平行四边形，‎ ‎∴∠HGF=∠HEF，‎ 故选D．‎ 点评：本题考查了等腰梯形的性质及三角形的中位线定理，解题的关键是利用中位线定理证得四边形为平行四边形．‎ ‎16.（2011•湖南张家界，6，3）顺次连接任意四边形四边中点所得的四边形一定是（　　）‎ A、平行四边形 B、矩形 C、菱形 D、正方形 考点：平行四边形的判定；三角形中位线定理。‎ 分析：顺次连接任意四边形四边中点所得的四边形，一组对边平行并且等于原来四边形某一对角线的一半，说明新四边形的对边平行且相等．所以是平行四边形．‎ 解答：解：根据三角形中位线定理，可知边连接后的四边形的两组对边相等，再根据平行四边形的判定可知，四边形为平行四边形．‎ 故选A．‎ 点评：本题用到的知识点为：三角形的中位线平行于第三边，且等于第三边的一半．‎ ‎17. 如图，D是△ABC内一点，BD⊥CD，AD=6，BD=4，CD=3，E、F、G、H分别是AB、AC、CD、BD的中点，则四边形EFGH的周长是（　　）‎ A、7 B、9 C、10 D、11‎ ‎【答案】D ‎【考点】三角形中位线定理；勾股定理．‎ ‎【专题】计算题．‎ ‎【分析】根据勾股定理求出BC的长，根据三角形的中位线定理得到HG= BC=EF，EH=FG= AD，求出EF、HG、EH、FG的长，代入即可求出四边形EFGH的周长．‎ ‎【解答】解：∵BD⊥DC，BD=4，CD=3，由勾股定理得：BC= =5， ∵E、F、G、H分别是AB、AC、CD、BD的中点， ∴HG= BC=EF，EH=FG= AD， ∵AD=6，∴EF=HG=2.5，EH=GF=3， ∴四边形EFGH的周长是EF+FG+HG+EH=2×（2.5+3）=11．故选D．‎ ‎【点评】本题主要考查对勾股定理，三角形的中位线定理等知识点的理解和掌握，能根据三角形的中位线定理求出EF、HG、EH、FG的长是解此题的关键．‎ ‎18. （2011广东省茂名，2，3分）如图，在△ABC中，D、E分别是AB、AC的中点，若DE=5，则BC=（　　）‎ ‎ A、6 B、8‎ ‎ C、10 D、12‎ 考点：三角形中位线定理。‎ 专题：计算题。‎ 分析：利用三角形的中位线定理求得BC即可．‎ 解答：解：∵D、E分别是AB、AC的中点，‎ ‎∴DE=BC，‎ ‎∵DE=5，‎ ‎∴BC=10．‎ 故选C．‎ 点评：此题主要是根据三角形的中位线定理进行分析计算．‎ ‎19. （2011浙江嘉兴，7，3分）如图，边长为4的等边△ABC中，DE为中位线，则四边形BCED的面积为（　　）‎ ‎ A． B． C． D． 考点：相似三角形的判定与性质；等边三角形的性质；三角形中位线定理．‎ 分析：根据边长为4的等边△ABC中，DE为中位线，得出DF=，再利用梯形的面积公式求出．‎ 解答：解：作DF⊥BC，‎ ‎∵边长为4的等边△ABC中，DE为中位线，∴DE=2，BD=2，∴DF=，‎ ‎∴则四边形BCED的面积为：DF×（DE+BC）=×（2+4）=3．故选B．‎ 点评：此题主要考查了等边三角形的性质以及三角形中位线的性质，得出根据DE为中位线，得出DF=是解决问题的关键．‎ ‎20. （2011浙江义乌，2，3分）如图，DE是△ABC的中位线，若BC的长为3cm，则DE的长是（　　）‎ ‎ A．2cm B．1.5cm C．1.2cm D．1cm 考点：三角形中位线定理。‎ 专题：计算题。‎ 分析：三角形中位线的性质：三角形的中位线平行于第三边，且等于第三边的一半；本题利用定理计算即可．‎ 解答：解：∵DE是△ABC的中位线，‎ ‎∴DE＝BC，‎ ‎∵BC的长为3cm，‎ ‎∴DE＝1.5．‎ 故选B．‎ 点评：本题考查了三角形的中位线定理，中位线是三角形中的一条重要线段，由于它的性质与线段的中点及平行线紧密相连，因此，它在几何图形的计算及证明中有着广泛的应用．‎ ‎21. （2011浙江舟山，7，3分）如图，边长为4的等边△ABC中，DE为中位线，则四边形BCED的面积为（　　）‎ ‎ A．2 B．3 C．4 D．6 考点：相似三角形的判定与性质；等边三角形的性质；三角形中位线定理。‎ 专题：计算题。‎ 分析：根据边长为4的等边△ABC中，DE为中位线，得出DF＝，再利用梯形的面积公式求出．‎ 解答：解：作DF⊥BC，‎ A B C E D F ‎∵边长为4的等边△ABC中，DE为中位线，‎ ‎∴DE＝2，BD＝2，‎ ‎∴DF＝，‎ ‎∴则四边形BCED的面积为：DF×（DE＋BC）＝×（2＋4）＝3．‎ 故选B．‎ 点评：此题主要考查了等边三角形的性质以及三角形中位线的性质，得出根据DE为中位线，得出DF＝是解决问题的关键．‎ 二、填空题 ‎1. （2011江苏淮安，10，3分）如图，在△ABC中，D、E分别是边AB、AC的中点，BC=8，则DE= .‎ 考点：三角形中位线定理。‎ 专题：计算题。‎ 分析：根据三角形的中位线定理得到DE=BC，即可得到答案．‎ 解答：解：∵D、E分别是边AB、AC的中点，BC=8，∴DE=BC=4．‎ 故答案为：4．‎ 点评：本题主要考查对三角形的中位线定理的理解和掌握，能正确运用三角形的中位线定理进行计算是解此题的关键．‎ ‎2. （2011江苏南京，10，2分）等腰梯形的腰长为5cm，它的周长是22cm，则它的中位线长为　6　cm．‎ 考点：梯形中位线定理；等腰梯形的性质。‎ 专题：计算题。‎ 分析：根据等腰梯形的腰长和周长求出AD+BC，根据梯形的中位线定理即可求出答案．‎ 解答：解：∵等腰梯形的腰长为5cm，它的周长是22cm，‎ ‎∴AD+BC=22﹣5﹣5=12，‎ ‎∵EF为梯形的中位线，‎ ‎∴EF=（AD+BC）=6．‎ 故答案为：6．‎ 点评：本题主要考查对等腰梯形的性质，梯形的中位线定理等知识点的理解和掌握，理解梯形的中位线定理[知道EF=（AD+BC）]是解此题的关键．‎ ‎3. （2011•江苏宿迁，11，3）将一块直角三角形纸片ABC折叠，使点A与点C重合，展开后平铺在桌面上（如图所示）．若∠C=90°，BC=8cm，则折痕DE的长度是　 　cm．‎ 考点：翻折变换（折叠问题）。‎ 专题：探究型。‎ 分析：根据图形翻折变换的性质可知DE是AC的垂直平分线，由于∠C是直角，故∠AED=90°，进而可得出DE是△ABC的中位线，由中位线定理即可得出结论．‎ 解答：解：∵点A与点C重合，‎ ‎∴DE是AC的垂直平分线，‎ ‎∵∠C是直角，‎ ‎∴∠AED=90°，‎ ‎∴DE是△ABC的中位线，‎ ‎∴DE=BC=×8=4cm．‎ 故答案为：4．‎ 点评：本题考查的是翻折变换及三角形中位线定理，熟知图形翻折变换的性质是解答此题的关键．‎ ‎4. （2011江苏连云港，16，3分）一等腰梯形两组对边中点连线段的平方和为8，则这个等腰梯形的对角线长为_______.‎ 考点：等腰梯形的性质；勾股定理；梯形中位线定理。‎ 专题：几何图形问题；数形结合。‎ 分析：首先由等腰梯形的性质，求得MN⊥BC，EF═（AD+BC），然后过点D作DK∥AC交BC的延长线于K，过点D作DH⊥BC于H，即可得四边形ACFD是平行四边形，四边形MNHD是矩形，则可得△BDK是等腰梯形，由三线合一的知识，可得BH=EF，在Rt△BDH中由勾股定理即可求得答案．‎ 解答：解：如图：‎ 已知：AD∥BC，AB=CD，E，N，F，M分别是边AB，BC，CD，DA的中点，且EF2+MN2=8．‎ 求：这个等腰梯形的对角长．‎ 解：过点D作DK∥AC交BC的延长线于K，过点D作DH⊥BC于H，‎ ‎∵AD∥BC，AB=CD，E，N，F，M分别是边AB，BC，CD，DA的中点，‎ ‎∴EF=（AD+BC），MN⊥BC，AC=BD，‎ ‎∴四边形ACFD是平行四边形，‎ ‎∴DK=AC=BD，CK=AD，‎ ‎∴BH=CH=BK=（BC+CK）=（BC+AD），‎ ‎∴BH=EF，‎ ‎∵四边形MNHD是矩形，‎ ‎∴DH=MN，‎ ‎∴在Rt△BDH中，BD2=BH2+DH2=EF2+MN2=8，‎ ‎∴BD=2．∴这个等腰梯形的对角长为2．‎ 故答案为：2．‎ 点评：此题考查了等腰梯形的性质，平行四边形与矩形的性质与判定以及等腰三角形，直角三角形的性质等知识．此题综合性很强，而且需要同学们将文字语言翻译成数学语言，难度较大，解题的关键是注意数形结合思想的应用，注意辅助线的作法．‎ ‎5. （2011江苏无锡，16，2分）如图，在Rt△ABC中，∠ACB=90°，D、E、F分别是AB、BC、CA的中点，若CD=5cm，则EF=　5　cm．‎ 考点：三角形中位线定理；直角三角形斜边上的中线。‎ 专题：几何图形问题。‎ 分析：已知CD是Rt△ABC斜边AB的中线，那么AB=2CD；EF是△ABC的中位线，则EF应等于AB的一半．‎ 解答：解：∵△ABC是直角三角形，CD是斜边的中线，‎ ‎∴CD=AB，‎ 又∵EF是△ABC的中位线，‎ ‎∴AB=2CD=2×5=10cm，‎ ‎∴EF=×10=5cm．‎ 故答案为：5‎ 点评：用到的知识点为：（1）直角三角形斜边的中线等于斜边的一半；（2）三角形的中位线等于对应边的一半．‎ ‎6.（2011巴彦淖尔，16，3分）如图，EF是△ABC的中位线，将△AEF沿AB方向平移到△EBD的位置，点D在BC上，已知△AEF的面积为5，则图中阴影部分的面积为　 　．‎ 考点：相似三角形的判定与性质；三角形中位线定理；平移的性质。‎ 专题：三角形。‎ 分析：由三角形的中位线的性质，得到EF∥BC，得出三角形相似，进一步利用平移的性质得出S△EBD=5，从而解决问题．‎ 解答：解：∵EF是△ABC的中位线，‎ ‎∴EF∥BC，‎ ‎∴△AEF∽△ABC，‎ ‎∴EF：BC=1：2，‎ ‎∴S△AEF：S△ABC=1：4，‎ ‎∵△AEF的面积为5，‎ ‎∴S△ABC=20，‎ ‎∵将△AEF沿AB方向平移到△EBD的位置，‎ ‎∴S△EBD=5，‎ ‎∴图中阴影部分的面积为：S△ABC﹣S△EBD﹣S△AEF=20﹣5﹣5=10．‎ 故答案为：10．‎ 点评：此题主要考查了三角形的中位线性质以及平移的性质、三角形相似的判定与性质等知识，根据平移性质得出S△EBD=5是解决问题的关键．‎ ‎7.（2011天津，14，3分）如图，点D、E、F分别是△ABC的边AB、BC、CA的中点，连接DE、EF、FD，则图中平行四边形的个数为　3　．‎ 考点：平行四边形的判定；三角形中位线定理。‎ 专题：推理填空题。‎ 分析：由已知点D、E、F分别是△ABC的边AB、BC、CA的中点，根据三角形中位线定理，可以推出EF∥AB且EF=AD，EF=DB，DF∥BC且DF=CE，所以得到3个平行四边形．‎ 解答：解：已知点D、E、F分别是△ABC的边AB、BC、CA的中点，‎ ‎∴EF∥AB且EF=AD，EF=DB，‎ DF∥BC且DF=CE，‎ ‎∴四边形ADEF、四边形BDFE和四边形CEDF为平行四边形，‎ 故答案为：3．‎ 点评：此题考查的是平行四边形的判定及三角形中位线定理，关键是有三角形中位线定理得出四边形的对边平行且相等而判定为平行四边形．‎ ‎8. （2011重庆江津区，13，4分）在梯形ABCD中，AD∥BC，中位线长为5，高为6，则它的面积是　30　．‎ 考点：梯形中位线定理。‎ 专题：计算题。‎ 分析：利用梯形的中位线的定义求得两底和，在利用梯形的面积计算方法计算即可．‎ 解答：解：∵中位线长为5，‎ ‎∴AD+BC＝2×5＝10，‎ ‎∴梯形的面积为：＝30，‎ 故答案为30．‎ 点评：本题考查的知识比较全面，需要用到梯形和三角形中位线定理以及平行四边形的性质．‎ ‎9. （2011•柳州）如图，要测量的A、C两点被池塘隔开，李师傅在AC外任选一点B，连接BA和BC，分别取BA和BC的中点E、F，量得E、F两点间的距离等于23米，则A、C两点间的距离　46　米．‎ 考点：三角形中位线定理。‎ 专题：计算题。‎ 分析：根据E、F分别是线段AB、BC中点，利用三角形中位线定理，即可求出AC的长．‎ 解答：解：∵E、F分别是线段AB、BC中点，‎ ‎∴FE是三角形ABC的中位线，‎ ‎∴FE=AC，‎ ‎∴AC=2FE=23×2=46米．‎ 故答案为46．‎ 点评：此题考查学生对三角形中位线定理的理解和掌握，要求学生熟练掌握三角形中位线定理，为进一步学习奠定基础．‎ ‎10.（2011•德州，10，4分）如图，D，E，F分别为△ABC三边的中点，则图中平行四边形的个数为 ．‎ 考点：平行四边形的判定；三角形中位线定理。‎ 专题：几何图形问题。‎ 分析：根据三角形中位线的性质定理，可以推出DE∥AF，DF∥EC，DF∥BE且DE=AF，DF=EC，DF=BE，根据平行四边形的判定定理，即可推出有三个平行四边形．‎ 解答：证明：∵D，E，F分别为△ABC三边的中点 ‎∴DE∥AF，DF∥EC，DF∥BE且DE=AF，DF=EC，DF=BE ‎∴四边形ADEF、DECF、DFEB分别为平行四边形 故答案为3．‎ 点评：本题主要考察平行四边的判定定理以及三角形中位线定理，关键在于找出相等而且平行的对边．‎ ‎11. （2011•山西18，3分）如图，已知AB=12；AB⊥BC于B，AB⊥AD于A，AD=5，BC=10．点E是CD的中点，则AE的长是 ．‎ 考点：勾股定理；三角形中位线定理。‎ 分析：首先做出辅助线连接DB，延长DA到F，使AD=DF．根据三角形中位线定理可得AE=CF，再利用勾股定理求出BD的长，然后证明可得到△FDC≌△BCD，从而得到FC=DB，进而得到答案．‎ 解答：解；连接DB，延长DA到F，使AD=DF．‎ ‎∵AD=5，‎ ‎∴DF=5，‎ ‎∵点E是CD的中点，‎ ‎∴AE=CF，‎ 在Rt△ABD中，‎ AD2+AB2=DB2，‎ ‎∴BD==13，‎ ‎∵AB⊥BC，AB⊥AD，‎ ‎∴AD∥BC，‎ ‎∴∠ADC=∠BCD，‎ 又∵DF=BC，DC=DC，‎ ‎∴△FDC≌△BCD，‎ ‎∴FC=DB=13，‎ ‎∴AE=．‎ 故答案为：．‎ 点评：此题主要考查了三角形中位线定理，勾股定理的综合运用，做题的关键是做出辅助线，证明BD=CF．‎ ‎12. （2011成都，12，4分）如图，在△ABC中，D，E分别是边AC．BC的中点，若DE＝4，则AB＝　　．‎ 考点：三角形中位线定理。‎ 专题：计算题。‎ 分析：根据三角形的中位线定理得到AB＝2DE，代入DE的长即可求出AB．‎ 解答：解：∵D，E分别是边AC，BC的中点，‎ ‎∴AB＝2DE，‎ ‎∵DE＝4，‎ ‎∴AB＝8．‎ 故答案为：8．‎ 点评：本题主要考查对三角形的中位线定理的理解和掌握，能熟练地运用三角形的中位线定理进行计算是解此题的关键．‎ ‎13. 2011黑龙江省哈尔滨,20，3分）如图，在Rt△ABC中，∠ACB=90°，点D是斜边AB的中点，DE⊥AC，垂足为E，若DE=2，CD=，则BE的长为　 ．‎ 考点：勾股定理；三角形中位线定理。‎ 分析：由点D为AB的中点，DE=2，求得BC，在直角三角形CDE中求得CE，在直角三角形CEB中从而求得BE得长．‎ 解答：解：∵点D为AB的中点，DE=2，‎ ‎∴BC=4，‎ ‎∵DE⊥AC，垂足为E，若DE=2，CD=，‎ 在直角三角形CDE中由勾股定理得CE=4，‎ ‎∵在Rt△ABC中，∠ACB=90°，‎ BE=．‎ 故答案为：4．‎ 点评：本题考查了勾股定理，本题考查了三角形中线性质，利用勾股定理求得．‎ 三、解答题 ‎1．（2011杭州，22，10分）在直角梯形ABCD中，AB∥CD，∠ABC=90°，AB=2BC=2CD，对角线AC与BD相交于点O，线段OA，OB的中点分别为E，F．‎ ‎ （1）求证：△FOE≌△DOC； （2）求sin∠OEF的值； （3）若直线EF与线段AD，BC分别相交于点G，H，求的值．‎ 考点：相似三角形的判定与性质；全等三角形的判定与性质；勾股定理；三角形中位线定理；直角梯形；锐角三角函数的定义．‎ 专题：证明题；代数几何综合题．‎ 分析：（1）由EF是△OAB的中位线，利用中位线定理，得EF∥AB，EF= AB，又CD∥AB，CD= AB，可得EF=CD，由平行线的性质可证△FOE≌△DOC； （2）由平行线的性质可知∠OEF=∠CAB，利用sin∠OEF=sin∠CAB=，由勾股定理得出AC与BC的关系，再求正弦值； （3））由（1）可知AE=OE=OC，EF∥CD，则△AEG∽△ACD，利用相似比可得EG= CD，同理得FH= CD，又AB=2CD，代入中求值．‎ 解答：解：（1）∵EF是△OAB的中位线， ∴EF∥AB，EF= AB， 而CD∥AB，CD=AB， ∴EF=CD，∠OEF=∠OCD，∠OFE=∠ODC， ∴△FOE≌△DOC； （2）∵在Rt△ABC中，AC= ， ∴sin∠OEF=sin∠CAB= ==； （3）∵AE=OE=OC，EF∥CD， ∴△AEG∽△ACD， ∴，即EG= CD， 同理FH= CD， ∴．‎ 点评：本题综合考查了全等三角形、相似三角形的判定与性质，勾股定理，中位线定理，锐角三角函数定义的运用．关键是由全等、相似得出相关线段之间的位置关系，数量关系．‎ ‎ ‎