兰州市2013年中考数学卷 11页

‎2013年兰州市初中毕业生学业考试 数 学（A）‎ 注意事项：‎ ‎1.全卷共150分，考试时间120分钟．‎ ‎2.考生必须将姓名、准考证号、考场、座位号等个人信息填（涂）写在答题卡上．‎ ‎3.考生务必将答案直接填（涂）写在答题卡的相应位置上．‎ 参考公式：二次函数顶点坐标公式：（，）‎ 一、选择题：本大题共15小题，每小题4分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．下图是由八个相同的小正方体组合而成的几何体，其左视图是 ‎ 正面 第1题图 A B C D ‎2．“兰州市明天降水概率是30%”，对此消息下列说法中正确的是 A．兰州市明天将有30%的地区降水 B．兰州市明天将有30%的时间降水 C．兰州市明天降水的可能性较小 D．兰州市明天肯定不降水 ‎3．二次函数的图象的顶点坐标是 A．（1，3） B．（，3） ‎ C．（1，） D．（，）‎ ‎4．⊙O1的半径为‎1cm，⊙O2的半径为‎4cm，圆心距O1O2=‎3cm，这两圆的位置关系是 A．相交 B．内切 ‎ C．外切 D．内含 ‎5．当时，函数的图象在 A．第四象限 B．第三象限 ‎ C．第二象限 D．第一象限 ‎ ‎6．下列命题中是假命题的是 A．平行四边形的对边相等 B．菱形的四条边相等 C．矩形的对边平行且相等 D．等腰梯形的对边相等 ‎7．某校九年级开展“光盘行动”宣传活动，各班级参加该活动的人数统计结果如下表，对于这组统计数据，下列说法中正确的是 班级 ‎1班 ‎2班 ‎3班 ‎4班 ‎5班 ‎6班 人数 ‎52‎ ‎60‎ ‎62‎ ‎54‎ ‎58‎ ‎62‎ A．平均数是58 B．中位数是‎58 ‎ C．极差是40 D．众数是60‎ ‎8．用配方法解方程时，配方后所得的方程为 A． B． C． D．‎ ‎9．△ABC中，、、分别是∠A、∠B、∠C的对边，如果，那么下列结论正确的是 A．sinA= B．cosB= C．tanA= D．tanB=‎ ‎10．据调查，2011年5月兰州市的房价均价为7600元/m2，2013年同期将达到8200元/m2，假设这两年兰州市房价的平均增长率为，根据题意，所列方程为 A． B．‎ C． 　 D．‎ ‎11．已知A（，），B（2，）两点在双曲线上，且，则的取值范围是 A． B． 　 C． D．‎ O 第13题图 B A 第12题图 ‎12．如图是一圆柱形输水管的横截面，阴影部分为有水部分，如果水面AB宽为‎8cm，水的最大深度为‎2cm，则该输水管的半径为 A．‎3cm 　　　 ‎ B．‎4cm 　　　 ‎ C．‎5cm 　　　 ‎ D．‎‎6cm ‎13．二次函数的图象如图所示．下列说法中 不正确的是 A． 　 B． ‎ C． 　　　 D．‎ ‎14．圆锥底面圆的半径为‎3cm，其侧面展开图是半圆，则圆锥母线长为 A．‎3cm　 　B．‎6cm　　 　C．‎9cm　 　　D．‎12cm ‎ O S t O S t O S t O S t A B C D A P B 第15题图 ‎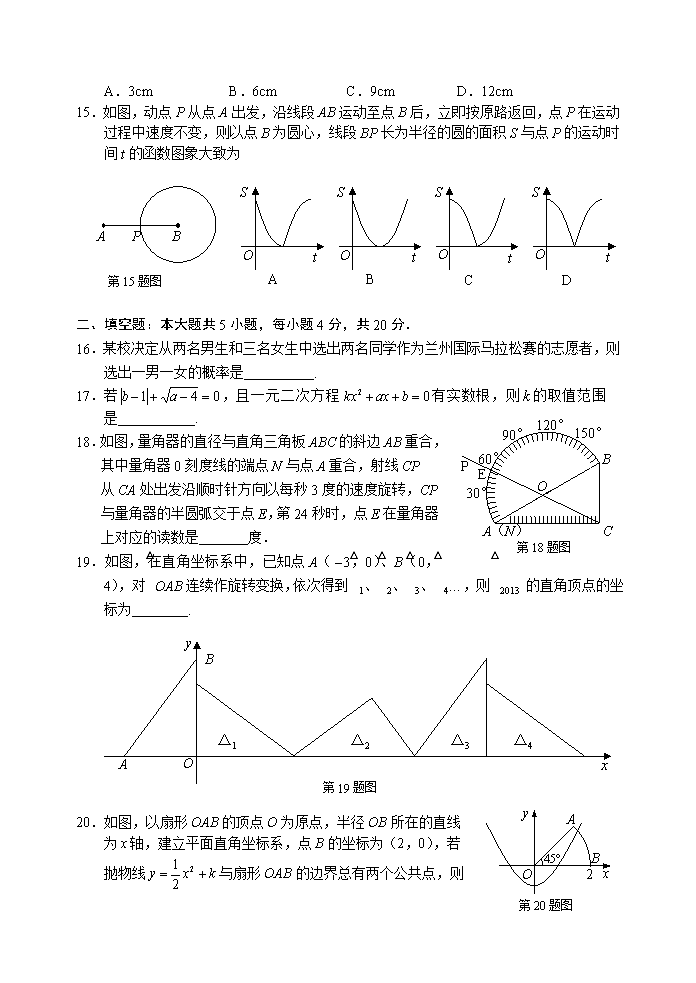15．如图，动点P从点A出发，沿线段AB运动至点B后，立即按原路返回，点P在运动过程中速度不变，则以点B为圆心，线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为 二、填空题：本大题共5小题，每小题4分，共20分．‎ ‎16．某校决定从两名男生和三名女生中选出两名同学作为兰州国际马拉松赛的志愿者，则选出一男一女的概率是　　　　　.‎ 第18题图 A（N）‎ CAAAAAA BAAAAAA OAAAAAA ‎30°‎ ‎60°‎ ‎90°‎ ‎120°‎ ‎150°‎ P EAAAAAA ‎17．若，且一元二次方程有实数根，则的取值范围 是 　　　　　.‎ ‎18．如图，量角器的直径与直角三角板ABC的斜边AB重合，其中量角器0刻度线的端点N与点A重合，射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转，CP与量角器的半圆弧交于点E，第24秒时，点E在量角器上对应的读数是　 　度．‎ ‎19．如图，在直角坐标系中，已知点A（，0）、B（0，4），对△OAB连续作旋转变换，依次得到△1、△2、△3、△4…，则△2013 的直角顶点的坐标为　　　　.‎ B A ‎△1‎ ‎△2‎ ‎△3‎ ‎△4‎ O 第19题图 y x O A A B A ‎45°‎ ‎22 ‎A 第20题图 ‎20．如图，以扇形OAB的顶点O为原点，半径OB所在的直线 为轴，建立平面直角坐标系，点B的坐标为（2，0），若 抛物线与扇形OAB的边界总有两个公共点，则 实数的取值范围是 .‎ 三、解答题：本大题共8小题，共70分．解答时写出必要的文字说明、证明过程或演算步骤．‎ ‎21．（本小题满分10分）‎ ‎（1）计算：‎ ‎（2）解方程：‎ A B O D C 第22题图 ‎22．（本小题满分5分）如图，两条公路OA和OB相交于O点，在∠AOB的内部有工厂C和D，现要修建一个货站P，使货站P到两条公路OA、OB的距离相等，且到两工厂C、D的距离相等，用尺规作出货站P的位置．（要求：不写作法，保留作图痕迹，写出结论.）‎ ‎23．（本小题满分6分）在兰州市开展的“体育、艺术2+1”活动中，某校根据实际情况，决定主要开设A：乒乓球，B：篮球，C：跑步，D：跳绳这四种运动项目．为了解学生喜欢哪一种项目，随机抽取了部分学生进行调查，并将调查结果绘制成如下的条形统计图和扇形统计图．请你结合图中信息解答下列问题：‎ ‎（1）样本中喜欢B项目的人数百分比是 ，其所在扇形统计图中的圆心角的度数是 ；‎ ‎（2）把条形统计图补充完整；‎ ‎（3）已知该校有1000人，根据样本估计全校喜欢乒乓球的人数是多少？‎ 项目 A B 人数（单位：人）‎ ‎10‎ C D ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎44‎ ‎8‎ ‎28‎ A ‎44%‎ D C B ‎28%‎ ‎8%‎ 第23题图 ‎ ‎ ‎24．（本小题满分8分）如图，在活动课上，小明和小红合作用一副三角板来测量学校旗杆高度．已知小明的眼睛与地面的距离（AB）是‎1.7m，他调整自己的位置，设法使得三角板的一条直角边保持水平，且斜边与旗杆顶端M在同一条直线上，测得旗杆顶端M仰角为45°；小红的眼睛与地面的距离（CD）是‎1.5m，用同样的方法测得旗杆顶端M的仰角为30°．两人相距‎28米且位于旗杆两侧（点B、N、D在同一条直线上）．求出旗杆MN的高度．（参考数据：，，结果保留整数．）‎ C D B N M A 小红 小明 第24题图 ‎25．（本小题满分9分）已知反比例函数的图象与一次函数的图象交于点A（1，4）和点B（，）．‎ ‎（1）求这两个函数的表达式；‎ ‎（2）观察图象，当>0时，直接写出>时自变量的取值范围；‎ ‎（3）如果点C与点A关于轴对称，求△ABC的面积．‎ B A B B O 第25题图 ‎26．（本小题满分10分）如图1，在△OAB中，∠OAB=90°，∠AOB=30°，OB=8．以OB为边，在△OAB外作等边△OBC，D是OB的中点，连接AD并延长交OC于E．‎ ‎（1）求证：四边形ABCE是平行四边形；‎ 第26题图 图1‎ A O B C D E 图2‎ G F A O B C ‎（2）如图2，将图1中的四边形ABCO折叠，使点C与点A重合，折痕为FG，求OG的长．‎ O G A B C F C O B A D M E N 第27题图 ‎27．（本小题满分10分）如图，直线MN交⊙O于A、B两点，AC是直径，AD平分∠CAM交⊙O于D，过D作DE⊥MN于E．‎ ‎（1）求证：DE是⊙O的切线；‎ ‎（2）若DE=‎6cm，AE=‎3cm，求⊙O的半径．‎ 第28题图 M C B O A D B B ‎28．（本小题满分12分）如图，在平面直角坐标系中，A、B为轴上两点，C、D为轴上的两点，经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线，我们把这条封闭曲线称为“蛋线”．已知点C的坐标为（0，），点M是抛物线C2：（＜0）的顶点．‎ ‎（1）求A、B两点的坐标；‎ ‎（2）“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由；‎ ‎（3）当△BDM为直角三角形时，求的值．‎ ‎2013年兰州市初中毕业生学业考试 ‎ 数学（A）参考答案及评分参考 本答案仅供参考，阅卷时会制定具体的评分细则和评分标准。‎ 一、 选择题:本大题共15小题，每小题4分，共60分.‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ 答案 B C A B A D A D A C D C D B B 二、填空题:本大题共5小题，每小题4分，共20分.‎ ‎16． 17． 18．144 ‎ ‎19．（8052，0） 20． ‎ 三、解答题:本大题共8小题，共70分.解答时写出必要的文字说明、证明过程或演算步 ‎ 骤.‎ ‎21.（本小题满分10分）‎ 解：（1）原式= ……………………………………………………………4分 ‎ =0 …………………………………………………………………………5分 ‎ （2）， ‎ ‎ ………………………………………………3分 ‎ ‎． ……………………………………………………5分 ‎ ‎22.（本小题满分5分）‎ 解：作出∠AOB的平分线、线段CD的垂直平分线（各2分）…………………………4分 结论……………………………………………………………………………………………5分 A B 人数（单位：人）‎ 项目 ‎10‎ C D ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎44‎ ‎8‎ ‎28‎ ‎20‎ ‎23.（本小题满分6分）‎ 解：（1）20%，72° …………………………2分 ‎ （2）如图 ……………………………4分 ‎ （3）440人 …………………………6分 M 小红 小明 E C D B N A F ‎24.（本小题满分8分）‎ 解： 过点A作AE⊥MN于E，‎ 过点C作CF⊥MN于F ……………………1分 则EF==0.2 ……………2分 在Rt△AEM中，‎ ‎∵∠MAE=45°，‎ ‎∴AE=ME …………………………………3分 设AE=ME=（不设参数也可）‎ ‎∴MF=＋0.2，CF=28 …………………………………………………………………4分 在Rt△MFC中，∠MFC=90°，∠MCF=30°‎ ‎∴MF=CF·tan∠MCF ……………………………………………………………………5分 ‎∴ …………………………………………………………………… 6分 ‎∴10.0　 …………………………………………………………………………………7分 ‎∴MN12 ……………………………………………………………………………………8分 答：旗杆高约为‎12米． ‎ A B B O D C B ‎25.（本小题满分9分）‎ 解：（1）∵点A（1，4）在的图象上，‎ ‎∴＝1×4＝4 ‎ ‎∴ ……………..……………1分 ‎∵点B在的图象上，∴ ‎ ‎∴点B（－2，－2） ………………….…2分 又∵点A、B在一次函数的图象上，‎ ‎∴ ‎ 解得 ……………………………………..………………………………….…3分 ‎∴ ………………………………………...………………………………4分 ‎∴这两个函数的表达式分别为：，‎ ‎（2）由图象可知，当 0＜＜1时，＞成立 ……………………………………5分 ‎（3）∵点C与点A关于轴对称，∴C（1，） ……………………………………6分 过点B作BD⊥AC，垂足为D，则D（1，）‎ 于是△ABC的高BD＝1＝3 ………………………………………….……..7分 ‎ 底为AC＝4＝8 …………………………………………………………………….. 8分∴S△ABC=AC·BD=×8×3=12 ……….………….…………….……………………..9分 图1‎ A O B C D E 图2‎ G F A O B C ‎26.（本小题满分10分）‎ ‎（1）证明：在Rt△OAB中，‎ D为OB的中点 ‎∴DO=DA ………………………..1分 ‎∴∠DAO=∠DOA =30°, ∠EOA=90° ‎ ‎∴∠AEO =60° ………………….2分 又∵△OBC为等边三角形 ‎∴∠BCO=∠AEO =60° …………………………………………………………….3分 ‎∴BC∥AE ……………….……………………………………………………….4分 ‎∵∠BAO=∠COA =90°‎ ‎∴OC∥AB ………………………………………………………………………….5分 ‎∴四边形ABCE是平行四边形． …………………………………………………6分 ‎（2）解：设OG=，由折叠可知：AG=GC=8－ …….…………………………7分 在Rt△ABO中 ‎∵∠OAB =90°，∠AOB =30°，OB=8‎ ‎∴OA=OB·cos30°=8×= .……………………………………………………..8分 在Rt△OAG中，OG2+OA2=AG2‎ ‎ ………………………,……………………………………….…..9分 解得，‎ ‎∴OG=1 …………………,……………………………………………….………………..10分 ‎27.（本小题满分10分）‎ ‎（1）证明：连接OD．‎ ‎∵OA=OD ‎∴∠OAD=∠ODA …………………….1分 C O B A D M E N ‎∵∠OAD=∠DAE ‎∴∠ODA=∠DAE ……………………..2分 ‎∴DO∥MN ……………………………3分 ‎∵DE⊥MN ‎∴∠ODE=∠DEM =90°‎ 即OD⊥DE ……………………………4分 ‎∴DE是⊙O的切线 ………………… 5分 ‎（2）解：连接CD．‎ ‎∵∠AED=90°，DE=6，AE=3‎ ‎∴AD= ……………………………………………………………………………...6分 ‎∵AC是⊙O的直径 ‎∴∠ADC=∠AED =90° …………………………………………………………………..7分 ‎∵∠CAD=∠DAE ‎ ‎∴△ACD∽△ADE ………………………………………………………………………..8分 ‎∴ 即 则AC=15 …………………………………………………………………………...9分 M C B O A D B B ‎∴⊙O的半径是‎7.5cm． …………………………………………………………………10分 ‎ ‎ ‎ ‎28.（本小题满分12分）‎ ‎(1)解：令=0，则 ‎ ‎∵＜0，∴‎ 解得：， ‎ ‎ ∴A（，0）、B（3，0） ……………………………2分 ‎（2）存在． ‎ ‎ ∵设抛物线C1的表达式为（），把C（0，）代入可得 ‎ ‎ ‎ ∴Ｃ1： …………………………………………………………4分 设P（，）‎ ‎∴ S△PBC = S△POC + S△BOP –S△BOC = …………………………………6分 ‎ ‎∵<0, ∴当时,S△PBC最大值为． ……………………………………7分 ‎（3）由C2可知： B（3，0），D（0，），M（1，）‎ BD2=， BM2=，DM2=， ‎ ‎∵∠MBD<90°, ∴讨论∠BMD=90°和∠BDM=90°两种情况．‎ 当∠BMD=90°时，BM2+ DM2= BD2 ，＋=‎ 解得：, (舍去) ………………………………………………………9分 当∠BDM=90°时，BD2+ DM2= BM2 ，＋=‎ 解得：， (舍去) ……………………………………………………11分 综上 ，时，△BDM为直角三角形． …………………………………12分