中考数学专题复习14动点坐标处理策略 含答案 3页

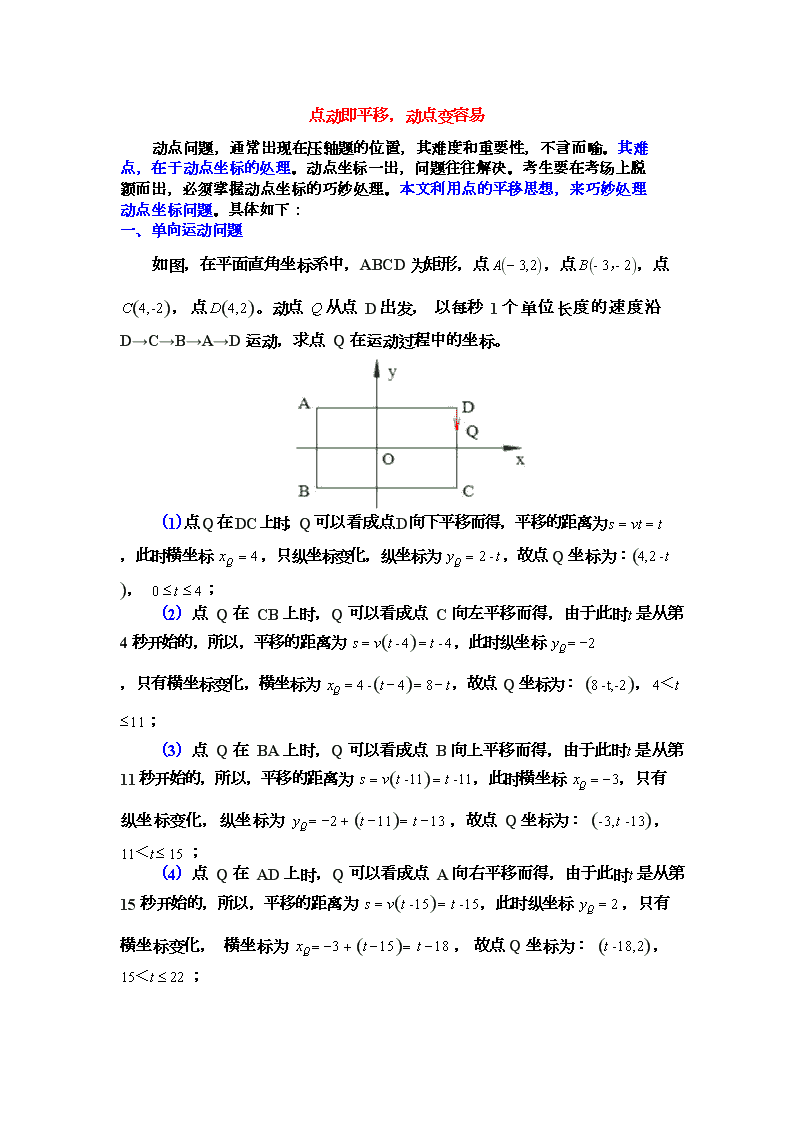
点动即平移，动点变容易 动点问题，通常出现在压轴题的位置，其难度和重要性，不言而喻。其难 点，在于动点坐标的处理。动点坐标一出，问题往往解决。考生要在考场上脱 颖而出，必须掌握动点坐标的巧妙处理。本文利用点的平移思想，来巧妙处理 动点坐标问题。具体如下：‎ 一、单向运动问题 如图，在平面直角坐标系中，ABCD 为矩形，点 A(- 3,2)，点 B(- 3，- 2)，点 C(4,-2) ， 点 D(4,2) 。动点 Q 从点 D 出发， 以每秒 1 个单位长度的速度沿 D→C→B→A→D 运动，求点 Q 在运动过程中的坐标。‎ ‎（1）点Q 在DC 上时，Q 可以看成点D 向下平移而得，平移的距离为 s = vt = t ，此时横坐标 xQ = 4 ，只纵坐标变化，纵坐标为 yQ = 2 - t ，故点 Q 坐标为：(4,2 - t )， 0 £ t £ 4 ；‎ ‎（2）点 Q 在 CB 上时，Q 可以看成点 C 向左平移而得，由于此时t 是从第 ‎4 秒开始的，所以，平移的距离为 s = v(t - 4) = t - 4 ，此时纵坐标 yQ = -2 ，只有横坐标变化，横坐标为 xQ = 4 - (t - 4)= 8 - t ，故点 Q 坐标为： (8 - t,-2)， 4＜t £ 11；‎ ‎（3）点 Q 在 BA 上时，Q 可以看成点 B 向上平移而得，由于此时t 是从第 ‎11 秒开始的，所以，平移的距离为 s = v(t -11) = t -11，此时横坐标 xQ = -3，只有 纵坐标变化，纵坐标为 yQ = -2 + (t -11)= t -13 ，故点 Q 坐标为： (- 3, t -13) ， 11＜t £ 15 ；‎ ‎（4）点 Q 在 AD 上时，Q 可以看成点 A 向右平移而得，由于此时t 是从第 ‎15 秒开始的，所以，平移的距离为 s = v(t -15) = t -15，此时纵坐标 yQ = 2 ，只有 横坐标变化， 横坐标为 xQ = -3 + (t -15)= t -18 ， 故点 Q 坐标为： (t -18,2) ， 15＜t £ 22 ；‎ 二、来回运动问题 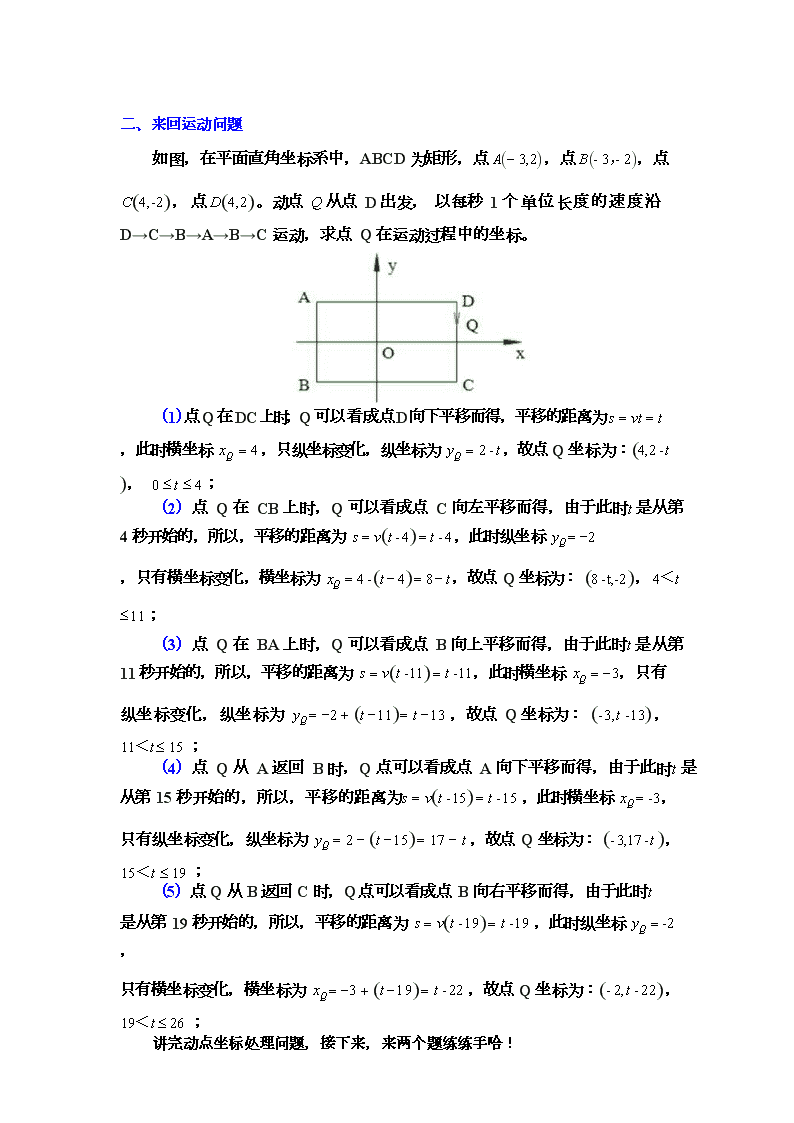如图，在平面直角坐标系中，ABCD 为矩形，点 A(- 3,2)，点 B(- 3，- 2)，点 C(4,-2) ， 点 D(4,2) 。动点 Q 从点 D 出发， 以每秒 1 个单位长度的速度沿 D→C→B→A→B→C 运动，求点 Q 在运动过程中的坐标。‎ ‎（1）点Q 在DC 上时，Q 可以看成点D 向下平移而得，平移的距离为 s = vt = t ，此时横坐标 xQ = 4 ，只纵坐标变化，纵坐标为 yQ = 2 - t ，故点 Q 坐标为：(4,2 - t )， 0 £ t £ 4 ；‎ ‎（2）点 Q 在 CB 上时，Q 可以看成点 C 向左平移而得，由于此时t 是从第 ‎4 秒开始的，所以，平移的距离为 s = v(t - 4) = t - 4 ，此时纵坐标 yQ = -2 ，只有横坐标变化，横坐标为 xQ = 4 - (t - 4)= 8 - t ，故点 Q 坐标为： (8 - t,-2)， 4＜t £ 11；‎ ‎（3）点 Q 在 BA 上时，Q 可以看成点 B 向上平移而得，由于此时t 是从第 ‎11 秒开始的，所以，平移的距离为 s = v(t -11) = t -11，此时横坐标 xQ = -3，只有 纵坐标变化，纵坐标为 yQ = -2 + (t -11)= t -13 ，故点 Q 坐标为： (- 3, t -13) ， 11＜t £ 15 ；‎ ‎（4）点 Q 从 A 返回 B 时，Q 点可以看成点 A 向下平移而得，由于此时t 是 从第 15 秒开始的，所以，平移的距离为s = v(t -15) = t -15 ，此时横坐标 xQ = -3， 只有纵坐标变化，纵坐标为 yQ = 2 - (t -15)= 17 - t ，故点 Q 坐标为： (- 3,17 - t )，‎ ‎15＜t £ 19 ；‎ ‎（5）点 Q 从 B 返回 C 时，Q 点可以看成点 B 向右平移而得，由于此时t 是从第 19 秒开始的，所以，平移的距离为 s = v(t -19) = t -19 ，此时纵坐标 yQ = -2 ，‎ 只有横坐标变化，横坐标为 xQ = -3 + (t -19)= t - 22 ，故点 Q 坐标为：(- 2, t - 22)， 19＜t £ 26 ；‎ 讲完动点坐标处理问题，接下来，来两个题练练手哈！‎ ‎【题 1】如图，在平面直角坐标系中，正方形 ABCD 中心在原点，且顶点 A 的坐标为(1,1)。动点 P、Q 分别从点 A、B 同时出发，绕着正方形的边按顺时针方向运动。当点 P 回到 A 点时，两点同时停止运动，设运动时间为t 秒。连接 OP、‎ OQ，线段 OP、OQ 与正方形围成的面积较小的部分的图形记为 M。‎ ‎⑴写出 B、C、D 三点的坐标；‎ ‎⑵若 P、Q 的速度为 1 个单位长度每秒，试判断在运动过程中，M 的面积是否发生变化？如不变，求出 M 的面积，若变化，请说明理由；‎ ‎⑶若 P 点的速度为 2 个单位长度每秒，Q 点的速度为 1 个单位长度每秒，当 M 的面积为 2 时，求t 的值。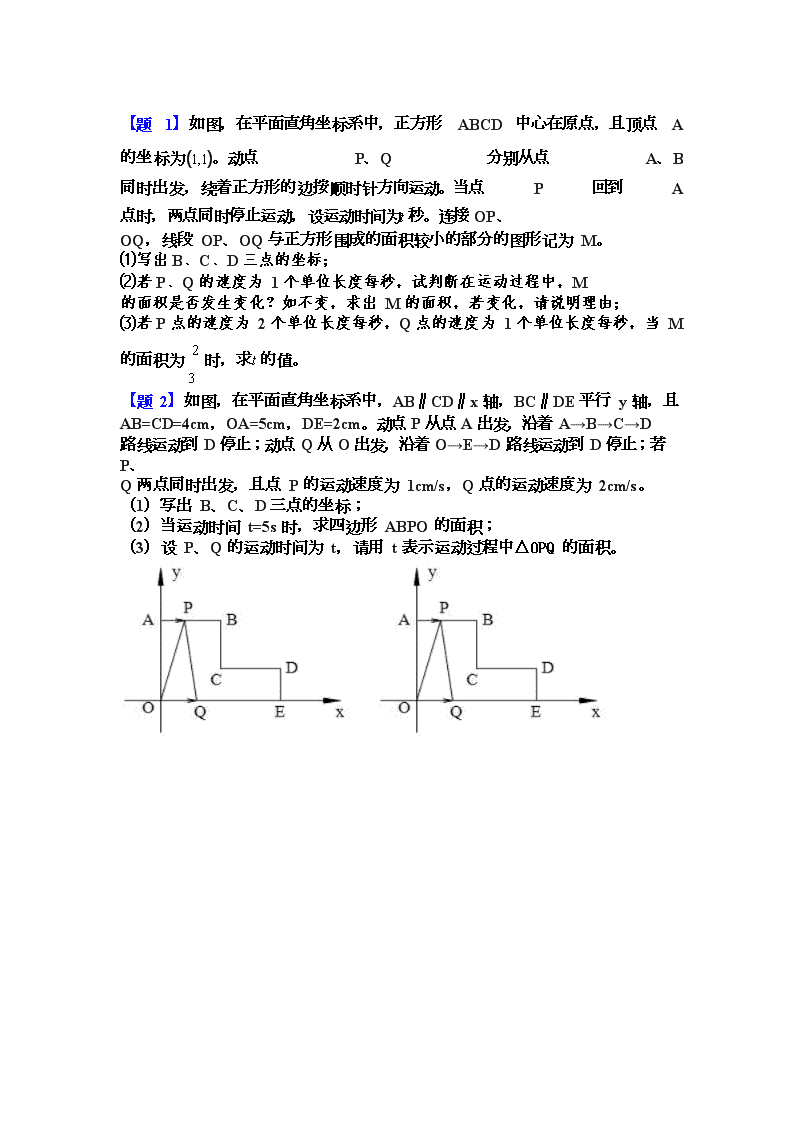‎ ‎3‎ ‎【题 2】如图，在平面直角坐标系中，AB∥CD∥x 轴，BC∥DE 平行 y 轴，且 AB=CD=4cm，OA=5cm，DE=2cm。动点 P 从点 A 出发，沿着 A→B→C→D 路线运动到 D 停止；动点 Q 从 O 出发，沿着 O→E→D 路线运动到 D 停止；若 P、‎ Q 两点同时出发，且点 P 的运动速度为 1cm/s，Q 点的运动速度为 2cm/s。‎ ‎（1）写出 B、C、D 三点的坐标；‎ ‎（2）当运动时间 t=5s 时，求四边形 ABPO 的面积；‎ ‎（3）设 P、Q 的运动时间为 t，请用 t 表示运动过程中△OPQ 的面积。‎