2014浙江省温州市中考数学试卷 13页

‎2014年浙江省温州市中考数学试卷 ‎（满分150分，考试时间120分钟）‎ 一、选择题（本大题共10小题，每小题4分，满分40分，在每小题给出的四个选项中，只有一项是符合题目要求的。）‎ ‎1. （2014浙江温州，1，4分）（－3）＋4的结果是（ ）‎ A．－7 B．－1 C．1 D．7‎ ‎【答案】C ‎2. （2014浙江温州，2，4分）右图是某班45名同学爱心捐款额的频数分布直方图（每组含前一个边界值，不含后一个边界值），则捐款人数最多的一组是（ ）‎ A．5～10元 B．10～15元 C．15～20元 D．20～25元 ‎【答案】C ‎3. （2014浙江温州，3，4分）如图所示的支架是由两个长方体构成的组合体，则它的主视图是（ ）‎ A． B． C． D．‎ ‎【答案】D ‎4. （2014浙江温州，4，4分）要使分式有意义，则的取值应满足（ ）‎ A． B． C． D．‎ ‎【答案】A ‎5. （2014浙江温州，5，4分）计算：的结果是（ ）‎ A． B． C． D．‎ ‎【答案】B ‎6. （2014浙江温州，6，4分）（小明记录了一星期每天的最高气温如下表，则这个星期每天的最高气温的中位数是（ ）‎ 星期 一 二 三 四 五 六 日 最高气温（℃）‎ ‎22‎ ‎24‎ ‎23‎ ‎25‎ ‎24‎ ‎22‎ ‎21‎ A．22℃ B．23℃ C．24℃ D．25℃‎ ‎【答案】B ‎7. （2014浙江温州，7，4分）一次函数的图象与轴交点的坐标是（ ）‎ A．（0，－4） B．（0，4） C．（2，0） D．（－2，0）‎ ‎【答案】B ‎8. （2014浙江温州，8，4分）如图，已知点，，在上，为优弧，下列选项中与相等的是（ ）‎ A． B． C． D．‎ ‎【答案】A ‎9. （2014浙江温州，9，4分）20位同学在植树节这天共种了52棵树苗，其中男生每人种3棵，女生每人种2棵．设男生有人，女生有人．根据题意，列方程组正确的是（ ）‎ A． B． C． D．‎ ‎【答案】D ‎10. （2014浙江温州，10，4分）如图，矩形的顶点在第一象限，∥轴，∥轴，且对角线的交点与原点重合．在边从小于到大于的变化过程中，若矩形的周长始终保持不变，则经过动点的反比例函数（）中的值得变化情况是（ ）‎ A．一直增大 B．一直减小 C．先增大后减小 D．先减小后增大 ‎【答案】C 二、填空题（本大题共6小题，每小题5分，满分30分.）‎ ‎11. 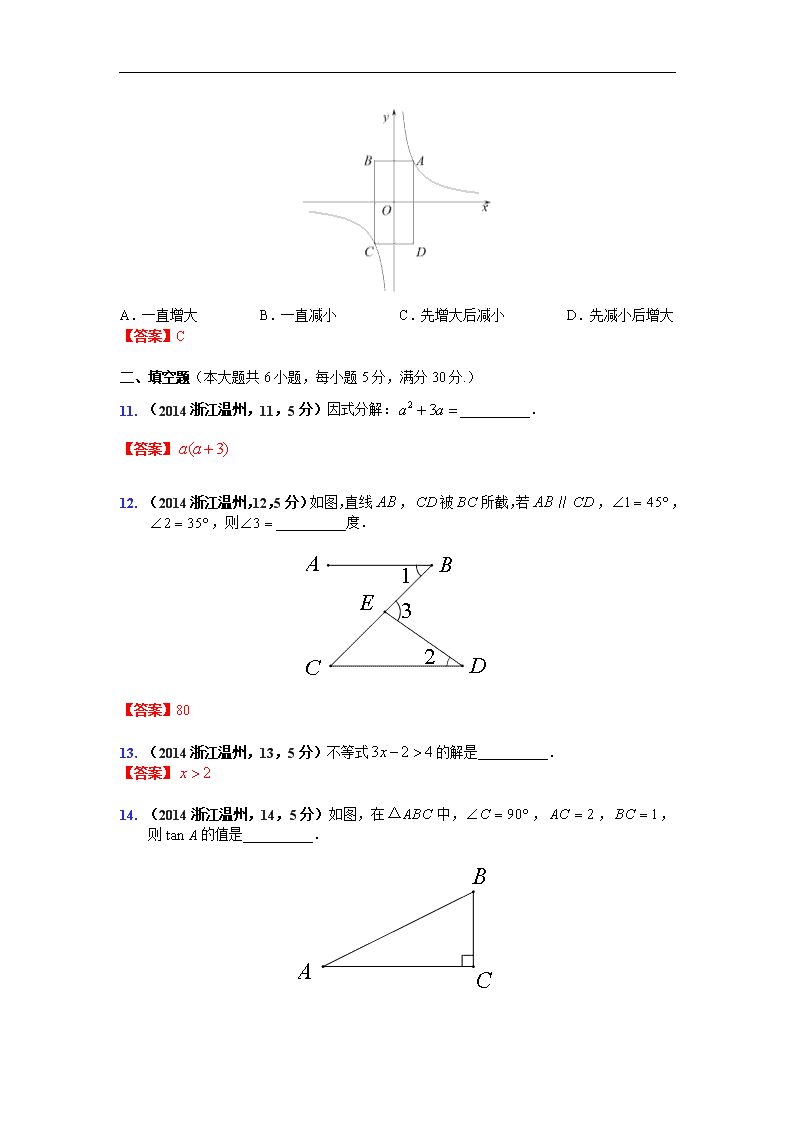（2014浙江温州，11，5分）因式分解：__________．‎ ‎【答案】‎ ‎12. （2014浙江温州，12，5分）如图，直线，被所截，若∥，，，则__________度．‎ ‎【答案】80‎ ‎13. （2014浙江温州，13，5分）不等式的解是__________．‎ ‎【答案】‎ ‎14. （2014浙江温州，14，5分）如图，在中，，，，则的值是__________．‎ ‎【答案】‎ ‎15. （2014浙江温州，15，5分）请举反例说明命题“对于任意实数，的值总是正数”是假命题，你举的反例是__________（写出一个的值即可）．‎ ‎【答案】－2（满足即可）‎ ‎16. （2014浙江温州，16，5分）_如图，在矩形中，是边上一点，且．经过点，与边所在的直线相切于点（为锐角），与边所在直线相交于另一点，且．当边或所在的直线与相切时，的长是__________．‎ ‎【答案】12或4‎ 三、解答题（本大题共8小题，满分80分，解答应写出文字说明、证明过程或演算步骤）‎ ‎17.‎ ‎（2014浙江温州，17（1），5分）（1）计算：；‎ ‎【答案】解：原式 ‎（2014浙江温州，17，5分）（2）化简：‎ ‎【答案】解：原式 ‎18. （2014浙江温州，18，8分）如图，在所给方格纸中，每个小正方形边长都是1，标号为①，②，③的三个三角形均为格点三角形（顶点在方格定点处），请按要求将图甲、图乙中的指定图形分割成三个三角形，使它们与标号为①，②，③的三个三角形分别对应全等．‎ ‎（1）图甲中的格点正方形；‎ ‎（2）图乙中的格点平行四边形．‎ ‎【答案】解：‎ ‎19. （2014浙江温州，19，8分）一个不透明的袋中装有20个只有颜色不同的球，其中5个黄球，8个黑球，7个红球．‎ ‎（1）求从袋中摸出一个球是黄球的概率；‎ ‎（2）现从袋中取出若干个黑球，搅匀后，使从袋中摸出一个球是黑球的概率是．求从袋中取出黑球的个数．‎ ‎【答案】解：‎ ‎（1）20个球里面有5个黄球，故；‎ ‎（2）设从袋中取出（，且为整数）个黑球，则此时袋中总共还有个球，黑球剩个．‎ ‎∵从袋中摸出一个球是黑球的概率是，∴，解得（经检验，符合实际）．‎ 答：从袋中取出黑球2个，可使得从袋中摸出一个黑球的概率是．‎ ‎20. （2014浙江温州，20，10分）如图，在等边三角形中，点，分别在边，上，且∥，过点作，交的延长线于点．‎ ‎（1）求的度数；‎ ‎（2）若，求的长．‎ ‎【答案】解：‎ ‎（1）∵三角形为等边三角形，‎ ‎∴，‎ ‎∵∥，‎ ‎∴，，‎ ‎∵，‎ ‎∴，‎ ‎∴．‎ ‎（2）∵，，‎ ‎∴，‎ ‎∴，‎ 又∵，‎ ‎∴三角形为等边三角形，‎ ‎∴，‎ ‎∴，‎ ‎∵，‎ ‎∴．‎ ‎21. （2014浙江温州，22，10分）如图，抛物线与轴交于，两点，它的对称轴与轴交于点，过顶点作轴于点，连接交于点．已知点的坐标为（－1，0）．‎ ‎（1）求该抛物线的解析式及顶点的坐标；‎ ‎（2）求与的面积之比．‎ ‎【答案】解：‎ ‎（1）∵抛物线与轴交于（－1，0），‎ ‎∴，解得，‎ ‎∴抛物线的解析式为．‎ ‎∵，‎ ‎∴顶点（1，4）．‎ ‎（2）由（1）得抛物线的对称轴为，即（1，0）．‎ ‎∵（－1，0），‎ ‎∴（3，0），‎ ‎∴．‎ 又∵轴于点，‎ ‎∴，∥轴，‎ ‎∴，‎ ‎∵，‎ ‎∴∽，‎ ‎∴．‎ 又∵，，‎ ‎∴．‎ ‎∴与的面积之比为1:4．‎ ‎22. （2014浙江温州，23，8分）勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感．他惊喜的发现：当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明．下面是小聪利用图1证明勾股定理的过程：‎ 将两个全等的直角三角形按图1所示摆放，其中，求证：．‎ 证明：连接，过点作边上的高，．‎ ‎∵，‎ 又∵，‎ ‎∴．‎ ‎∴．‎ 请参照上述证法，利用图2完成下面的证明．‎ 将两个全等的直角三角形按图2所示摆放，其中．‎ 求证：．‎ 证明：连接_______________________________________．‎ ‎∵___________________________________，‎ 又∵_________________________________，‎ ‎∴_______________________________________________．‎ ‎∴．‎ ‎【答案】证明：‎ 连接，过点作边上的高，．．‎ ‎∵，‎ 又∵，‎ ‎∴．‎ ‎∴．‎ ‎23. （2014浙江温州，24，12分）八（1）班五位同学参加学校举办的数学素养竞赛．试卷中共有20道题，规定每题答对得5分，答错扣2分，未答得0分．赛后，，，，五位同学对照评分标准回忆并记录了自己的答题情况（同学只记得有7道题未答），具体如下表：‎ 参赛同学 答对题数 答错题数 未答题数 ‎19‎ ‎0‎ ‎1‎ ‎17‎ ‎2‎ ‎1‎ ‎15‎ ‎2‎ ‎3‎ ‎17‎ ‎1‎ ‎2‎ ‎/‎ ‎/‎ ‎7‎ ‎（1）根据以上信息，求，，，四位同学成绩的平均分；‎ ‎（2）最后获知，，，，五位同学的成绩分别是95分，81分，64分，83分，58分．‎ ‎①求同学的答对题数和答错题数；‎ ‎②经计算，，，，思维同学实际成绩的平均分是80.75分，与（1）中算得的平均分不相符，发现是其中一位同学记错了自己的答题情况．请指出哪位同学记错了，并写出他的实际答题情况（直接写出答案即可）．‎ ‎【答案】解：‎ ‎（1）同学的成绩为：，同学的成绩为：，同学的成绩为：，同学的成绩为：．‎ ‎，，，四位同学成绩的平均分．‎ 答：，，，四位同学成绩的平均分为82.5分．‎ ‎（2）‎ ‎①设同学答对道题，则答错题数为．‎ 由题意可得，解得．‎ 答：同学答对题数为12，答错题数为1．‎ ‎②同学的成绩记错了．‎ 设同学答对道题，答错道题．‎ 则，即有．‎ ‎∵，且、为整数，故可行解只有，．‎ 答：同学答对14道题，答错3道题，未答3道题．‎ ‎24. （2014浙江温州，25，14分）如图，在屏幕直角坐标系中，点，的坐标分别为（－3，0），（0，6）．动点从点出发，沿轴正方向以每秒1个单位的速度运动，同时动点从点出发，沿射线方向以每秒2个单位的速度运动，以，为邻边构造□，在线段延长线上取点，使．设点运动时间为秒．‎ ‎（1）当点运动到线段的中点时，求的值及点的坐标；‎ ‎（2）当点在线段上时，求证：四边形为平行四边形；‎ ‎（3）在线段上取点，使，过点作，截取，，且点，分别在一、四象限．在运动过程中，设□的面积为．‎ ‎①当点，中有一点落在四边形的边上时，求出所有满足条件的的值；‎ ‎②若点，中恰好只有一个点落在四边形的内部（不包括边界）时，直接写出的取值范围．‎ ‎【答案】解：‎ 由题意得：，，，，‎ ‎（1）∵（0，6），‎ ‎∴，‎ 当点运动到线段的中点时，，‎ ‎∴．‎ 此时，，‎ ‎∴（0，）．‎ ‎（2）∵四边形为平行四边形，‎ ‎∴，，‎ ‎∴‎ 即，‎ 又∵，‎ ‎∴≌，‎ ‎∴，，‎ ‎∴∥，‎ ‎∴四边形是平行四边形．‎ ‎（3）‎ 由题意可得（0，），（，0），（，），（，0），‎ ‎（，0），（，2），（，0－1）．‎ ‎①‎ 情况一：当在轴上方时 ‎（a）在上时，∵轴，轴，∴∽，∴，即有，解得；‎ ‎（b）在上时，∵轴，轴，∴∽，∴，即有，解得；‎ 情况二：当在轴上方时 ‎（a）在上时，∵轴，轴，∴∽，∴，即有，解得；‎ ‎（b）在上时，∵轴，轴，∴∽，∴‎ ‎，即有，解得；‎ 综上，当、、、时，点，中有一点落在四边形的边上．‎ ‎②‎ 情况一：如下第一幅图，当时，恰好过，当时，在四边形外部，而在四边形内部，直到时，点恰好在上，故；‎ 此时，；‎ 如下第二幅图，当时，恰好过，当时，在四边形内部，而在四边形外部，直到时，点恰好在上，故；‎ 此时，．‎ 综上，当点，中恰好只有一个点落在四边形的内部（不包括边界）时，或．‎