中考数学模拟试题6无答案 3页

九年级数学模拟试题（6）‎ 一、选择题 ‎1.下列计算结果正确的是( )‎ ‎ A． B． C． D．‎ ‎2.在下列四个图案中既是轴对称图形，又是中心对称图形的是( )‎ x y O ‎3.右图所示的几何体是由一些小立方块搭成的，则这个几何体的俯视图是( )‎ ‎ A. B. C. D.‎ ‎4.已知反比例函数，下列结论不正确的是( )‎ ‎ A．图象必经过点(-1,2) B．y随x的增大而增大 ‎ C．图象在第二、四象限内 D．若x＞1，则y＞-2‎ ‎5.已知圆锥的底面半径长为5，侧面展开后得到一个半圆，则该圆锥的母线长为( )‎ ‎ A．2.5 B．‎5 C．10 D．15‎ ‎6.二次函数的图象如图所示，则一次函数的图象不经过( )‎ ‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎7.已知是二元一次方程组的解，则的算术平方根为( )‎ ‎ A．4 B．‎2 C． D． ±2‎ ‎8.一个边长为2的正多边形的内角和是其外角和的2倍，则这个正多边形的半径是( )‎ ‎ A．2 B． C．1 D． ‎9.如图，在△ABC 中，∠C=Rt∠，∠B=30°，边AB 的垂直平分线DE 交AB 于点E，交BC 于点D，CD=3，则BC 的长为( ) ‎ A.6 B. C.9 D. ‎ ‎10.货车和小汽车同时从甲地出发,以各自的速度匀速向乙地行驶,小汽车到达乙地后,立即以相同的速度沿原路返回甲地.已知甲、乙两地相距180 千米，货车的速度为60 千米/小时,小汽车的速度为90 千米/小时,则下图中能分别反映出货车、小汽车离乙地的距离y(千米)与各自行驶时间t(小时)之间的函数图象是( )‎ 二、填空题 ‎11.分解因式：22＋4＋2＝ ．‎ ‎12．当宽为‎3cm的刻度尺的一边与圆相切时，另一边与圆的两个交点处的读数如图所示（单位：cm），那么该圆的半径为 cm．‎ ‎13. 化简的结果是____________．‎ A D B C E F P ‎14．如图，在矩形ABCD中，AB=3，AD=4，点P在AD上，PE⊥AC于E，PF⊥BD于F，则PE+PF等于 ‎ A B C ‎(B)‎ D A B C ‎(D)‎ ‎…‎ ‎(A)‎ D l ‎15. 将边长为‎8cm的正方形ABCD的四边沿直线l向右滚动(不滑动)，当正方形滚动两周时，正方形的顶点A所经过的路线的长是 cm 三、解答题（解答要写出必要的文字说明、证明过程或推演步骤）‎ ‎16. 先化简，再求值：，其中 ‎17.‎2010年5月1日，第41届世博会在上海举办，世博知识在校园迅速传播.小明同学就本班学生对世博知识的了解程度进行了一次调查统计，下图是他采集数据后绘制的两幅不完整的统计图（A：不了解，B：一般了解，C：了解较多，D：熟悉）.请你根据图中提供的信息解答以下问题：‎ ‎（1）求该班共有多少名学生；‎ ‎（2）在条形统计图中，将表示“一般了解”的部分补充完整；‎ ‎（3）在扇形统计图中，计算出“了解较多”部分所对应的圆心角的度数；‎ ‎（4）从该班中任选一人，其对世博知识的了解程度为“熟悉”的概率是多少？‎ A B C D 了解程度 人数 ‎5‎ ‎10‎ ‎15‎ ‎20‎ ‎25‎ A ‎10%‎ B ‎30%‎ D C ‎18.为打造“书香校园”，某学校计划用不超过1900本科技类书籍和1620本人文类书籍，组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本，人文类书籍50本；组建一个小型图书角需科技类书籍30本，人文类书籍60本．‎ ‎（1）问符合题意的组建方案有几种？请你帮学校设计出来；‎ ‎（2）若组建一个中型图书角的费用是860元，组建一个小型图书角的费用是570元，试说明在（1）中哪种方案费用最低？最低费用是多少元？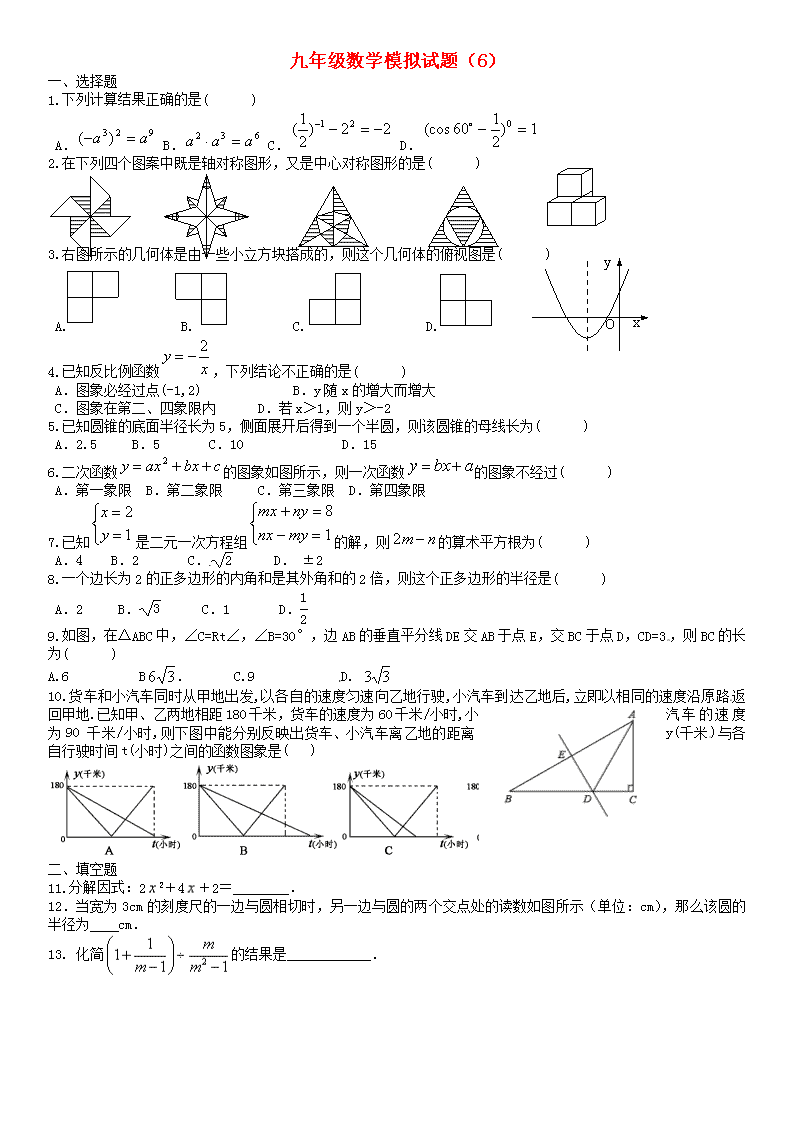‎ ‎19、如图，O是△ABC的内心，BO的延长线和△ABC的外接圆相交于D，连接DC、DA、OA、OC，四边形OADC为平行四边形。‎ ‎（1）求证：△BOC≌△CDA ‎（2）若AB=2，求阴影部分的面积。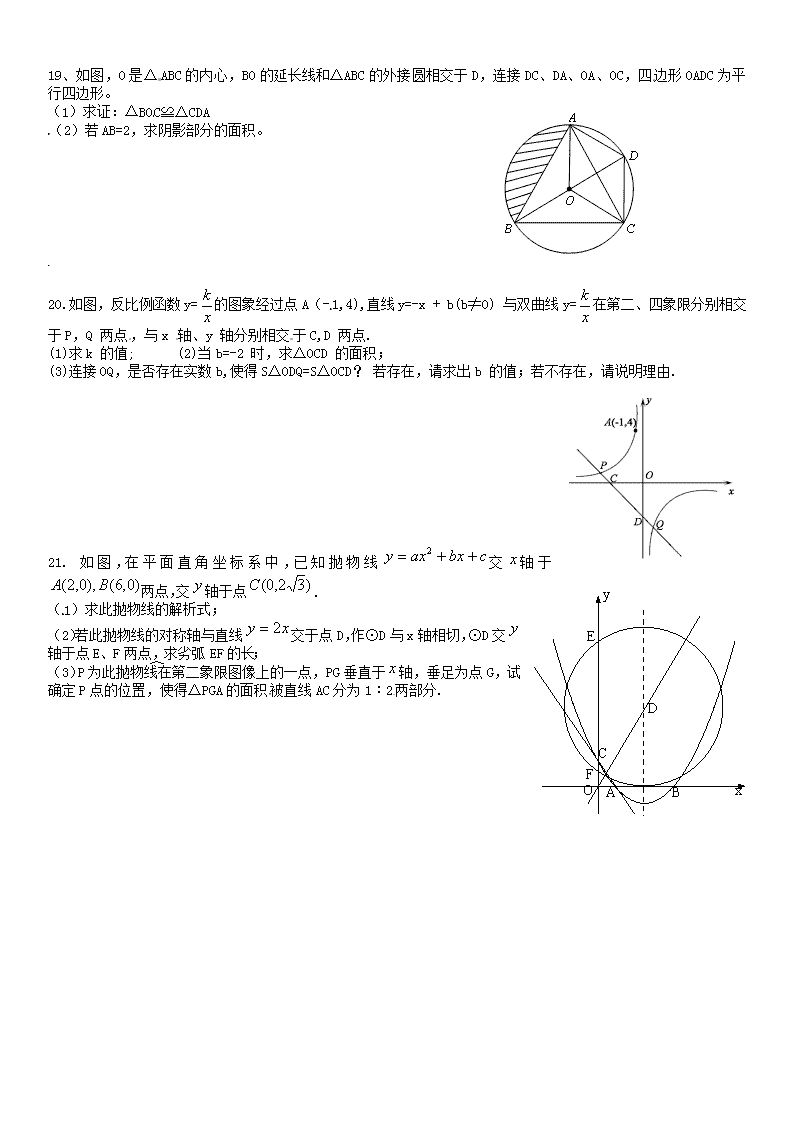‎ ‎20.如图，反比例函数y=的图象经过点A（-1,4),直线y=-x + b(b≠0) 与双曲线y=在第二、四象限分别相交于P，Q 两点，与x 轴、y 轴分别相交于C,D 两点.‎ ‎(1)求k 的值; (2)当b=-2 时，求△OCD 的面积；‎ ‎(3)连接OQ，是否存在实数b,使得S△ODQ=S△OCD？ 若存在，请求出b 的值；若不存在，请说明理由. ‎ x y O A C B D E F ‎21. 如图，在平面直角坐标系中，已知抛物线交轴于两点，交轴于点.‎ ‎（1）求此抛物线的解析式；‎ ‎（2）若此抛物线的对称轴与直线交于点D，作⊙D与x轴相切，⊙D交轴于点E、F两点，求劣弧EF的长；‎ ‎（3）P为此抛物线在第二象限图像上的一点，PG垂直于轴，垂足为点G，试确定P点的位置，使得△PGA的面积被直线AC分为1︰2两部分.‎