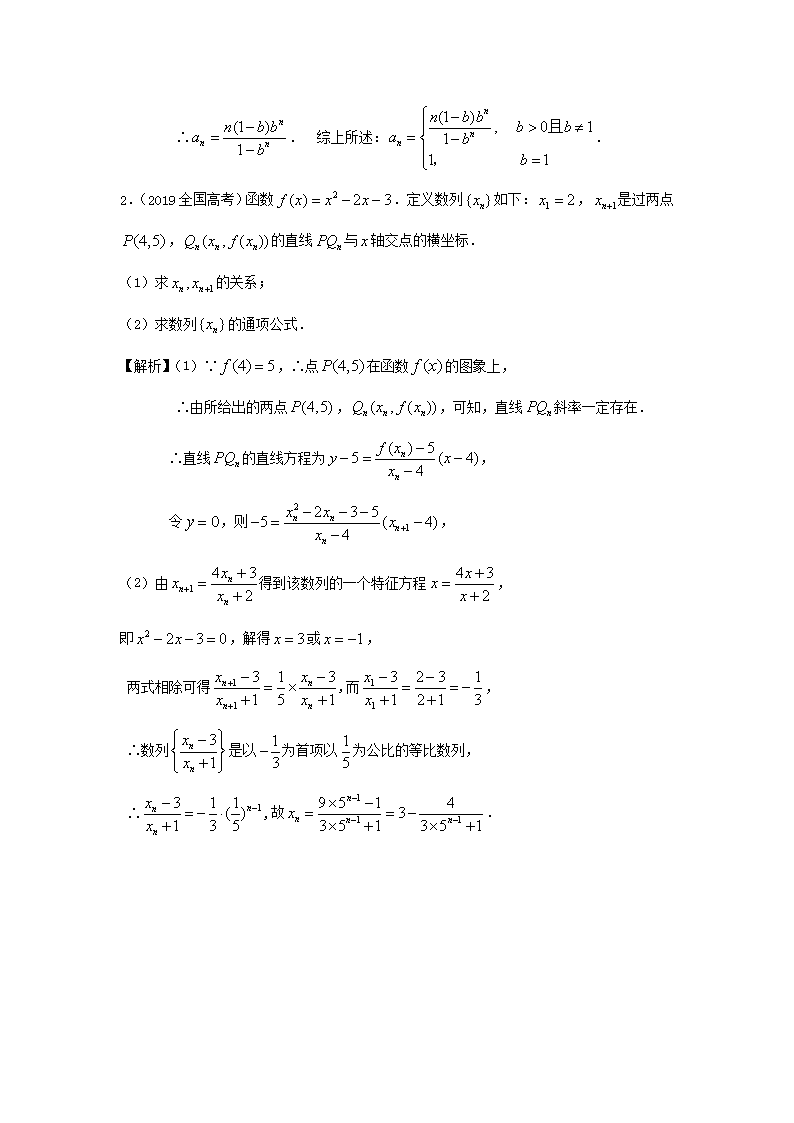三维设计广东文人教版2014高考数学第一轮复习考案 递推数列求通项1 文 3页

第44课 递推数列求通项（1）‎ ‎【补充题型】‎ ‎1．递推公式形如（其中p、q、r、h均为常数，且）‎ 方法：作特征方程，解出．‎ ‎【例1】已知数列满足：对于都有．‎ ‎（1）若，求； （2）若，求．‎ ‎【解析】作特征方程，∴，∴．‎ ‎（1）∵，∴．‎ ‎（2）∵，∴，‎ ‎ ∴数列是以为首项，以为公差的等差数列，‎ ‎∴数列从第5项开始都不存在，∴当，时，．‎ ‎【变式】已知数列满足性质：对于，且，求的通项公式．‎ ‎【解析】作特征方程，∴，解得或．‎ ‎∴数列是以为首项，以为公比的等比数列，‎ ‎2．递推公式形如 方法：①设，‎ ‎②解出，的值，其中，满足，‎ ‎③再用换元法转化为等比数列求解．‎ ‎【例2】（2019汕头质检）已知数列中，，，求.‎ ‎【解析】设，∴． ‎ ‎∴或，取，则，‎ ‎ ∴是以首项为，公比为的等比数列，‎ ‎∵，又，‎ ‎∴数列是以为首项，为公比的等比数列，‎ ‎【变式】已知数列中，，，，求.‎ ‎【解析】设，‎ ‎∴或，取，‎ 则，‎ ‎ ∴是以首项为，公比为的等比数列，‎ 又由得．‎ ‎【课时作业】‎ ‎1．（2019广东高考）设，数列满足，．‎ 求数列的通项公式；‎ ‎【解析】∵，∴， ∴． ‎ ① 当时，，则是以1为首项，1为公差的等差数列 ． ‎ ‎∴，即． ‎ ② 当且时，． ‎ 当时，，‎ ‎∴是以为首项，为公比的等比数列． ‎ ‎∴． 综上所述：．‎ ‎2．（2019全国高考）函数．定义数列如下：，是过两点，的直线与轴交点的横坐标．‎ ‎（1）求的关系；‎ ‎（2）求数列的通项公式．‎ ‎【解析】（1）∵，∴点在函数的图象上，‎ ‎∴由所给出的两点，，可知，直线斜率一定存在．‎ ‎∴直线的直线方程为，‎ 令，则，‎ ‎（2）由得到该数列的一个特征方程，‎ 即，解得或，‎ 两式相除可得,而，‎ ‎∴数列是以为首项以为公比的等比数列，‎ ‎∴,故．‎